Содержание
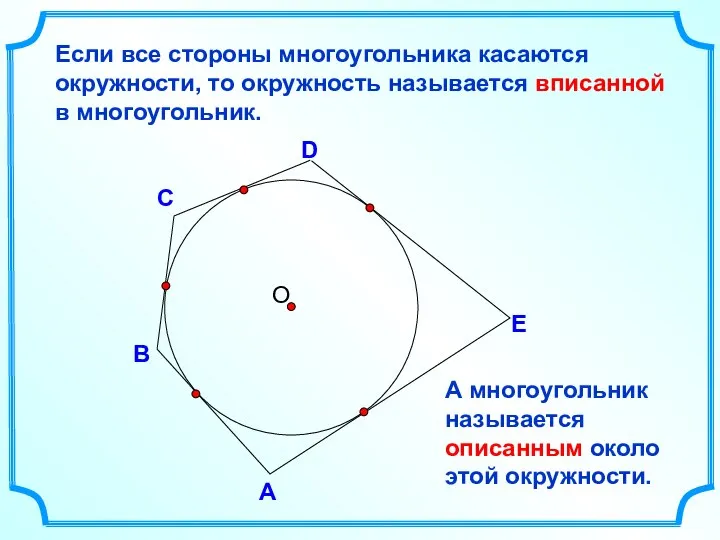
- 2. D В С Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник. А
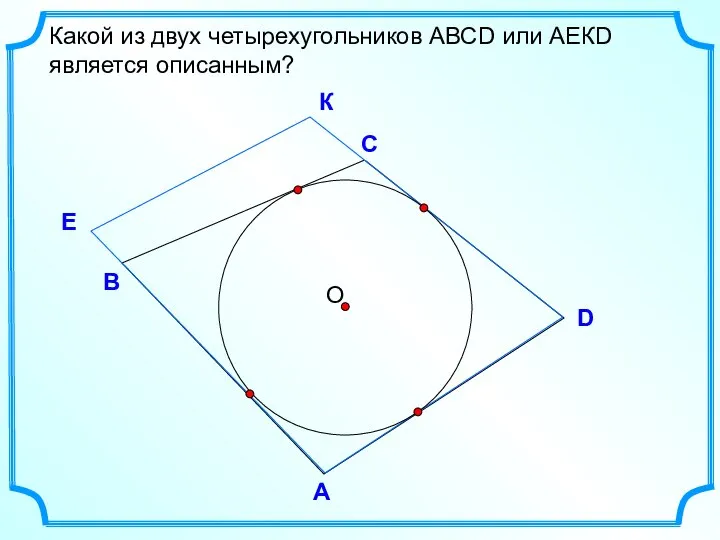
- 3. D В С Какой из двух четырехугольников АВСD или АЕКD является описанным? А E К
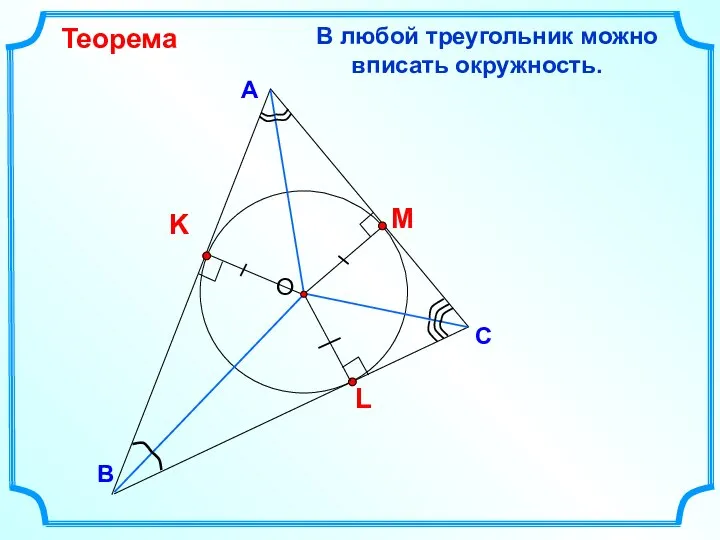
- 4. В С А В любой треугольник можно вписать окружность. Теорема
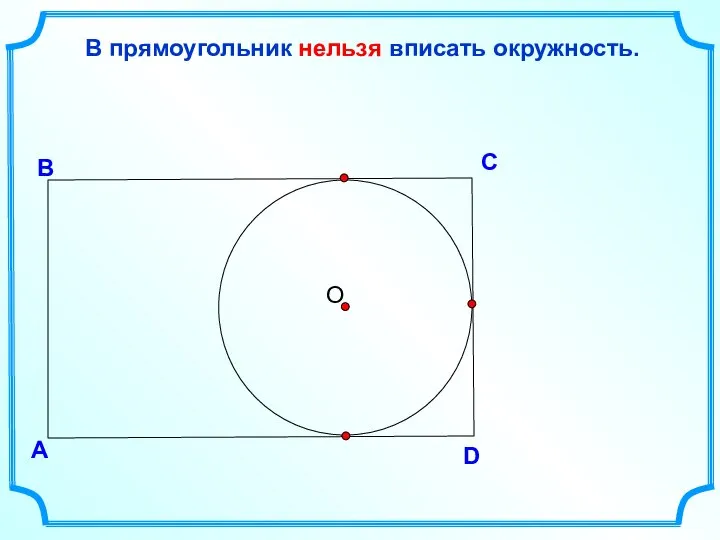
- 5. D В С В прямоугольник нельзя вписать окружность. А
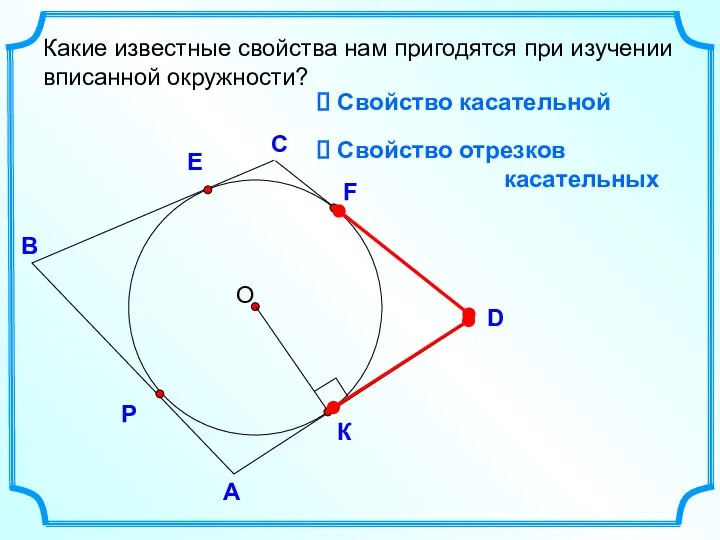
- 6. D В С Какие известные свойства нам пригодятся при изучении вписанной окружности? А E Свойство касательной
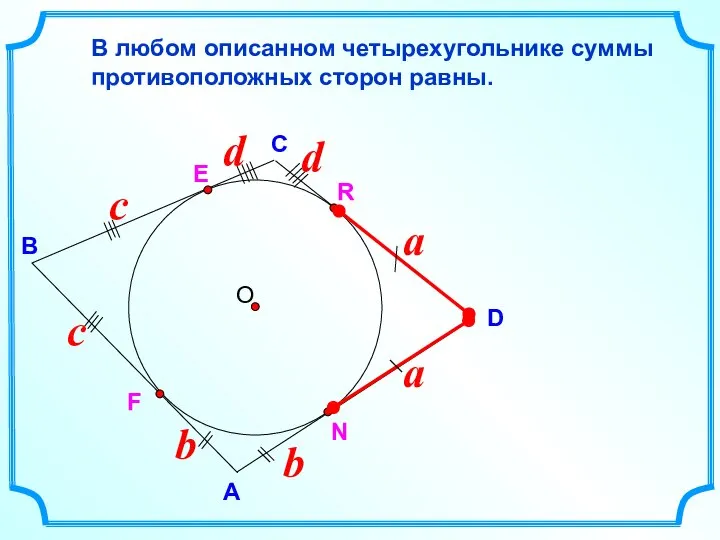
- 7. D В С В любом описанном четырехугольнике суммы противоположных сторон равны. А E R N F
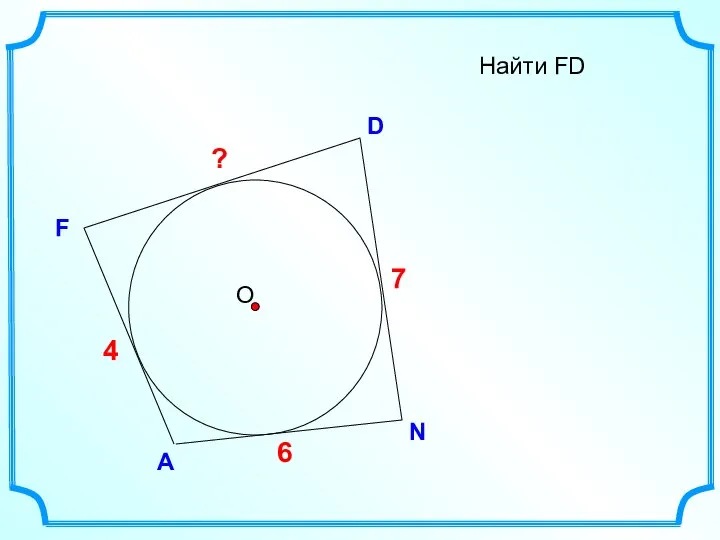
- 8. D F Найти FD А N ? 4 7 6
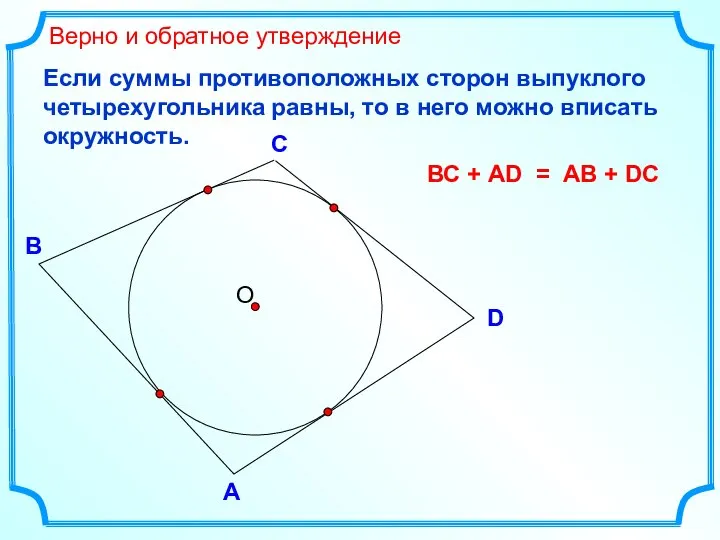
- 9. D В С Верно и обратное утверждение А Если суммы противоположных сторон выпуклого четырехугольника равны, то
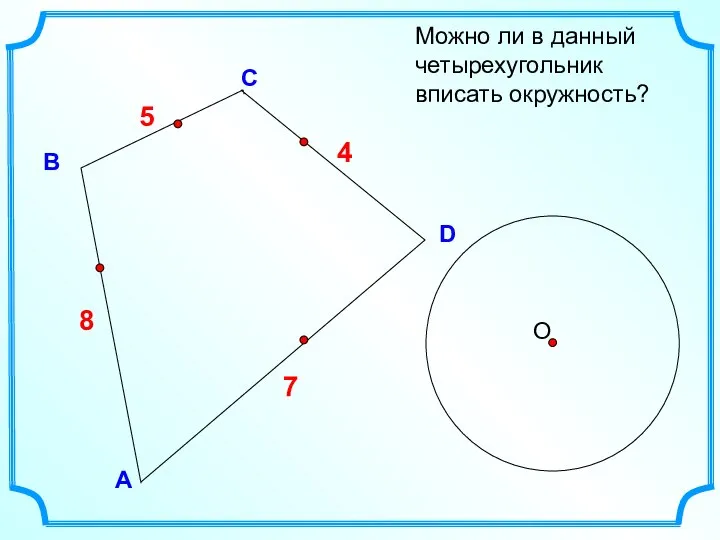
- 10. D В С Можно ли в данный четырехугольник вписать окружность? А 5 7 4 8
- 11. Построить три треугольника (остроугольный, прямоугольный тупоугольный). Провести биссектрисы углов. Отметить центр окружности в каждом треугольнике. Провести
- 12. № 689 Решить в тетради задачу:
- 14. Скачать презентацию


 Многоугольники в нашей жизни
Многоугольники в нашей жизни Разложение вектора по двум неколлинеарным векторам
Разложение вектора по двум неколлинеарным векторам Квадратичная функция. Наглядно-методическое пособие. 9 класс
Квадратичная функция. Наглядно-методическое пособие. 9 класс XII командный турнир по математике Математические бои
XII командный турнир по математике Математические бои Пирамида. Элементы пирамиды. Поверхность пирамиды
Пирамида. Элементы пирамиды. Поверхность пирамиды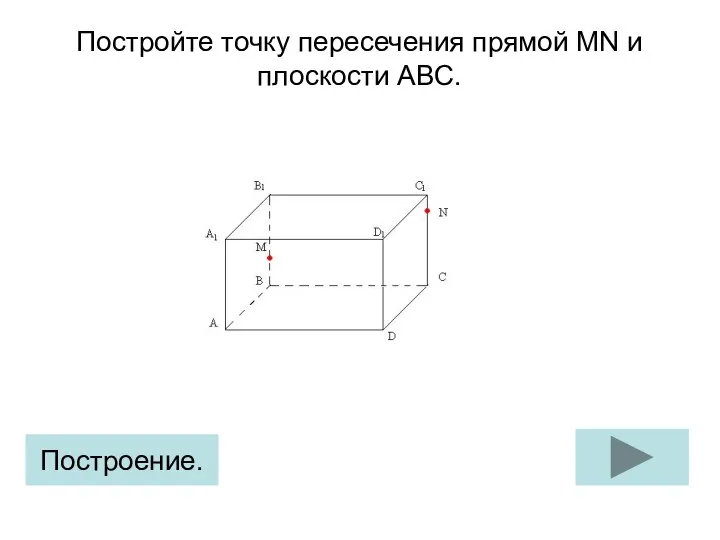 Точка пересечения прямой MN и плоскости ABC. Построение (задание 2)
Точка пересечения прямой MN и плоскости ABC. Построение (задание 2) Внеклассное мероприятие по математике с элементами экономики. В отделении Сбербанка. 5 класс
Внеклассное мероприятие по математике с элементами экономики. В отделении Сбербанка. 5 класс Переводчицы. Задача
Переводчицы. Задача Подумай. Вопросы. Тесты
Подумай. Вопросы. Тесты Вычисления вида 32 + 8, 40 – 8
Вычисления вида 32 + 8, 40 – 8 Следствия из теорем синусов и косинусов
Следствия из теорем синусов и косинусов Условная оптимизация. Лекция 11
Условная оптимизация. Лекция 11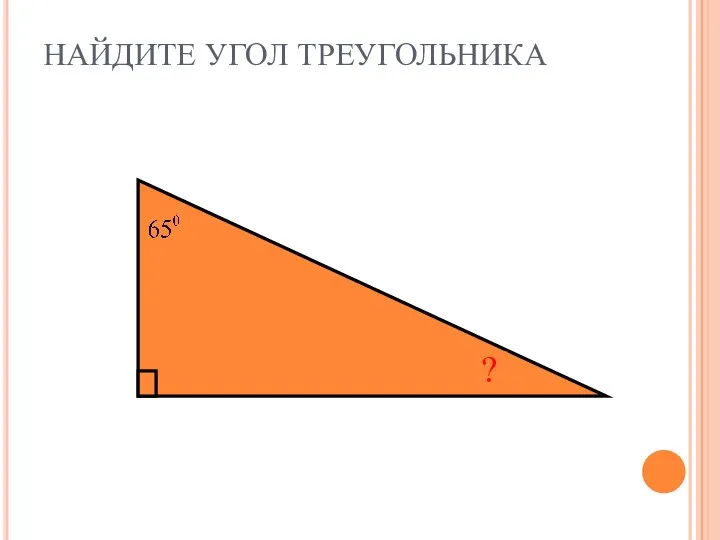 Нахождение угла треугольника
Нахождение угла треугольника Существование треугольника, равного данному (7 класс)
Существование треугольника, равного данному (7 класс) Окружность и круг
Окружность и круг Аттестационная работа. Сослужит ли добрую службу математика экологии
Аттестационная работа. Сослужит ли добрую службу математика экологии Математика и Незнайка. Математическая сказка
Математика и Незнайка. Математическая сказка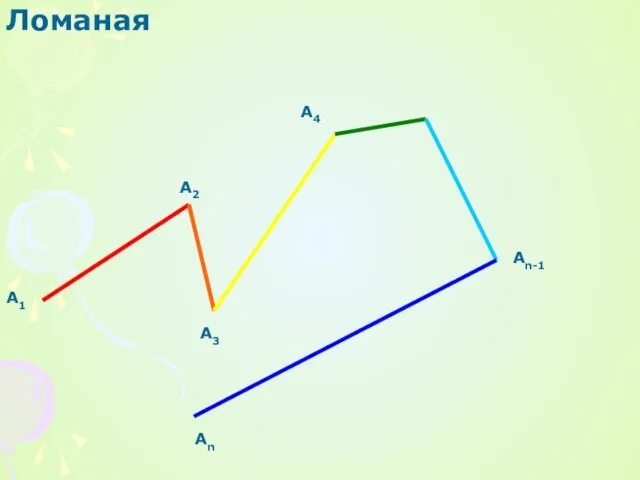 Презентация на тему Ломаная
Презентация на тему Ломаная  Основы геометрии
Основы геометрии История дифференциального исчисления
История дифференциального исчисления Построение графиков функций
Построение графиков функций Цифра в 21 веке
Цифра в 21 веке Карточки по математике
Карточки по математике Окружность и длина окружности
Окружность и длина окружности Прямоугольник. Ось симметрии
Прямоугольник. Ось симметрии Расчёт скорости официанта от кассы до столика
Расчёт скорости официанта от кассы до столика Методы решения логарифмических уравнений. 11 класс
Методы решения логарифмических уравнений. 11 класс Площадь параллелограмма и ромба
Площадь параллелограмма и ромба