Содержание
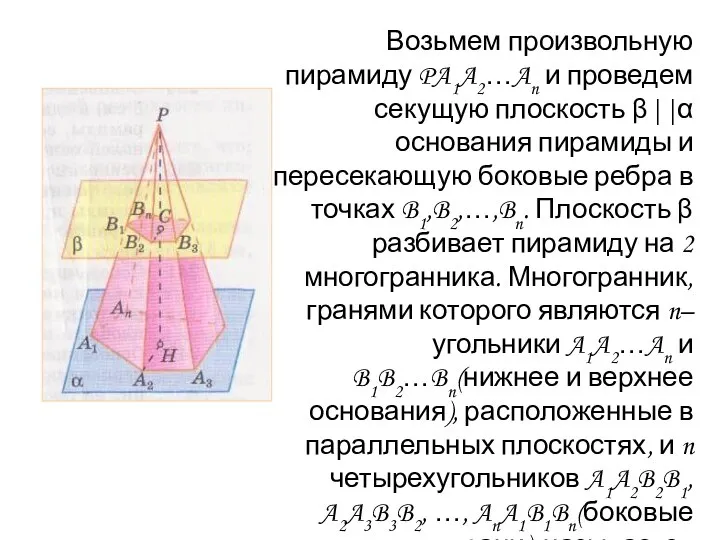
- 2. Возьмем произвольную пирамиду PA1A2…An и проведем секущую плоскость β||α основания пирамиды и пересекающую боковые ребра в
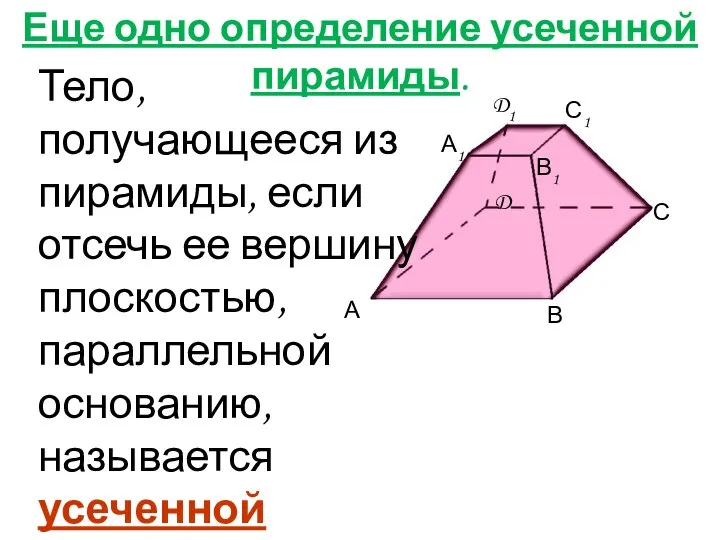
- 3. Еще одно определение усеченной пирамиды. Тело, получающееся из пирамиды, если отсечь ее вершину плоскостью, параллельной основанию,
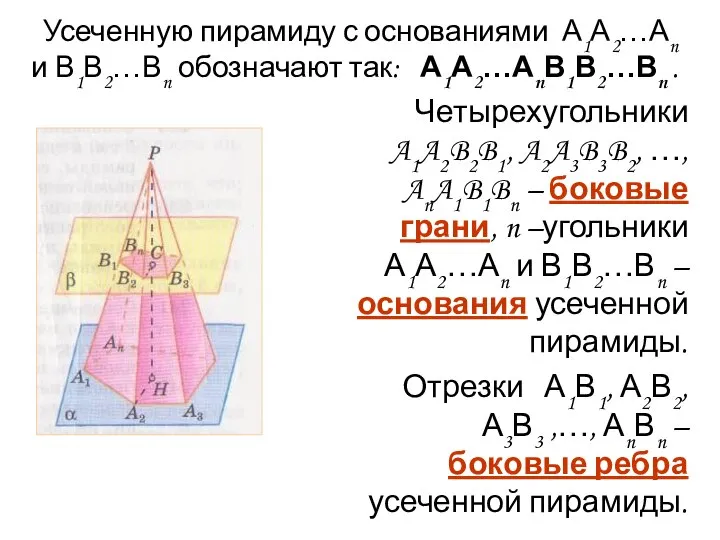
- 4. Четырехугольники A1A2B2B1, A2A3B3B2, …, AnA1B1Bn – боковые грани, n –угольники А1А2…Аn и В1В2…Вn – основания усеченной
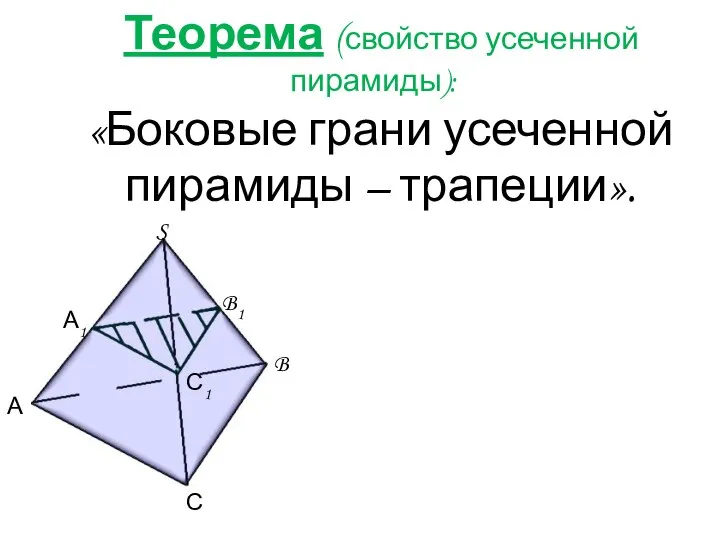
- 5. Теорема (свойство усеченной пирамиды): «Боковые грани усеченной пирамиды – трапеции».
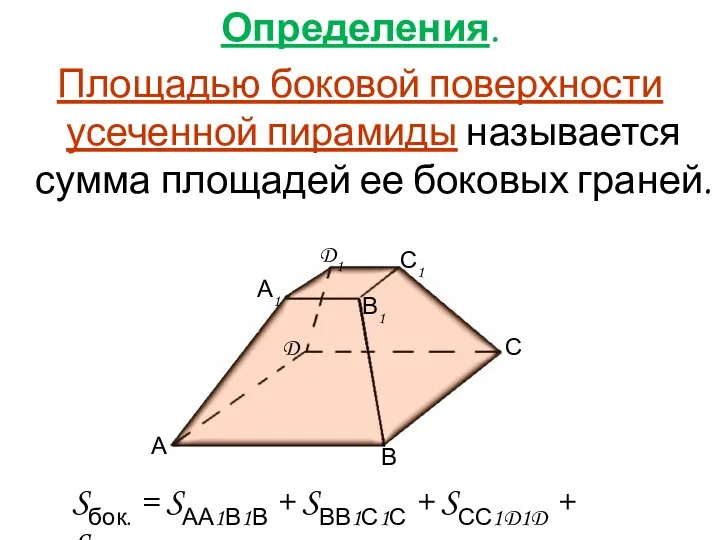
- 6. Определения. Площадью боковой поверхности усеченной пирамиды называется сумма площадей ее боковых граней. Sбок. = SАА1В1В +
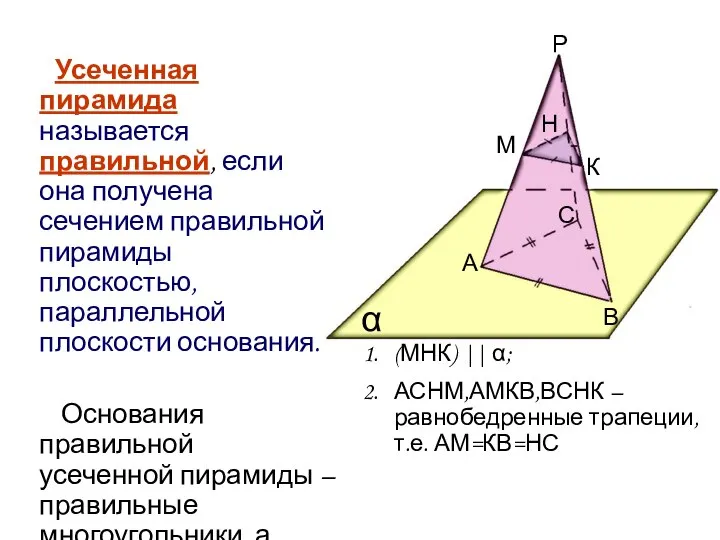
- 7. Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной плоскости основания. Основания правильной
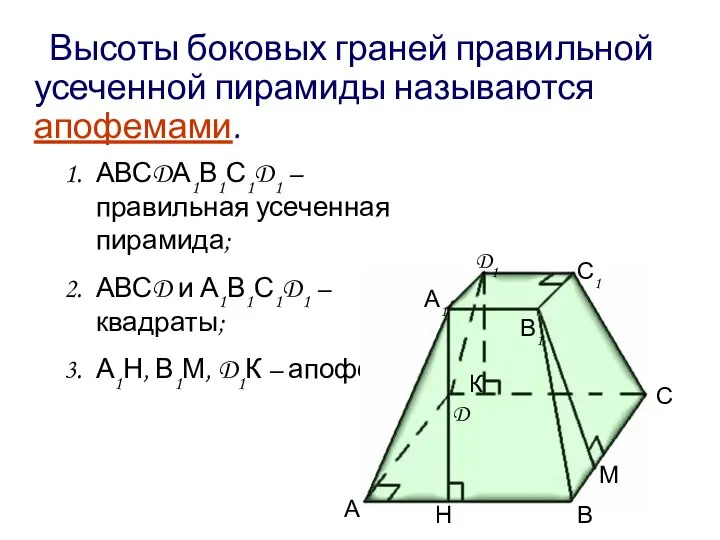
- 8. Высоты боковых граней правильной усеченной пирамиды называются апофемами. АВСDА1В1С1D1 – правильная усеченная пирамида; АВСD и А1В1С1D1
- 9. Теорема: «Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему». Sбок. пр.
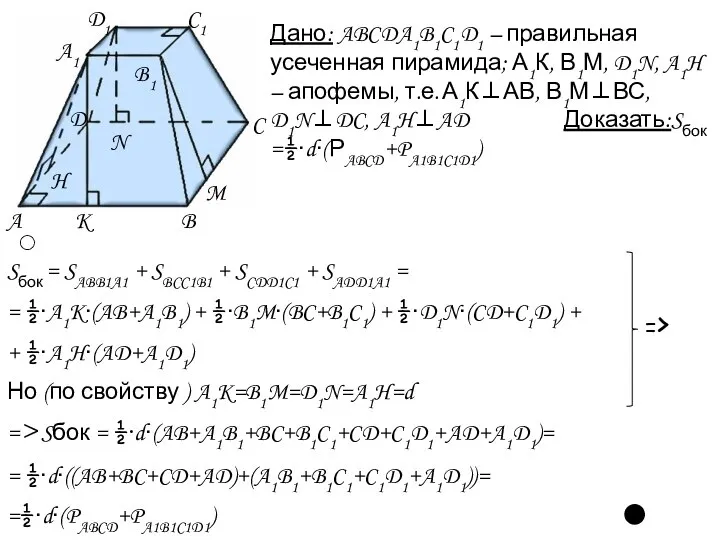
- 10. Дано: ABCDA1B1C1D1 – правильная усеченная пирамида; А1К, В1М, D1N, A1H – апофемы, т.е. А1К⊥АВ, В1М⊥ВС, D1N⊥DC,
- 12. Скачать презентацию

 Десятичные дроби. Уравнения
Десятичные дроби. Уравнения Смежные и вертикальные углы
Смежные и вертикальные углы Презентация на тему Дробь как одна или несколько равных долей
Презентация на тему Дробь как одна или несколько равных долей  Взвешенные графы. Остовные деревья. Кратчайшие пути
Взвешенные графы. Остовные деревья. Кратчайшие пути Секреты квадратных уравнений
Секреты квадратных уравнений Область определения и множество значений тригонометрических функций
Область определения и множество значений тригонометрических функций Презентация на тему Сложение отрицательных и положительных чисел
Презентация на тему Сложение отрицательных и положительных чисел  Моделирование. Объекты и их модели. (Тема 10)
Моделирование. Объекты и их модели. (Тема 10)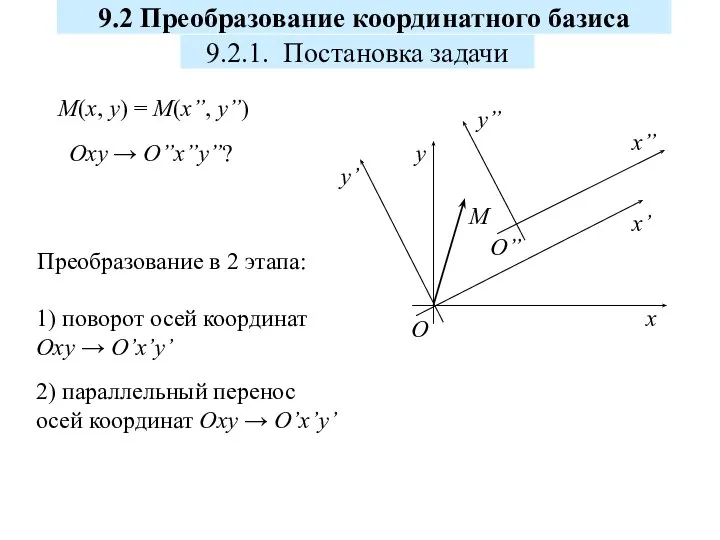 Преобразование координатного базиса
Преобразование координатного базиса Угол между векторами
Угол между векторами Равносильные уравнения и неравенства
Равносильные уравнения и неравенства 1 признак подобия треугольников
1 признак подобия треугольников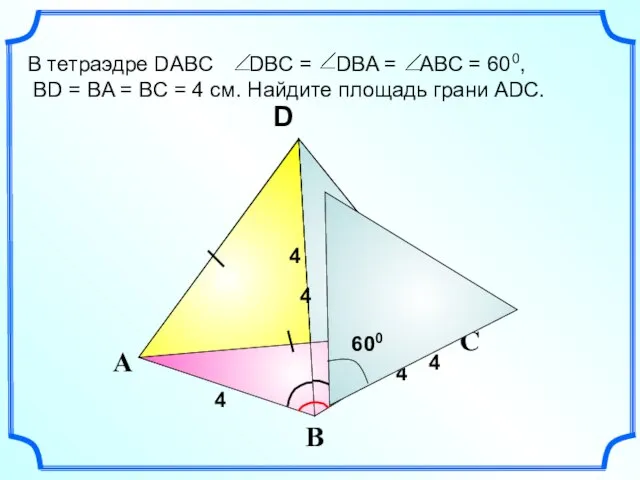 Тетраэдр. Свойства тетраэдра
Тетраэдр. Свойства тетраэдра Обыкновенные и десятичные дроби
Обыкновенные и десятичные дроби Симметрия. Симметрия относительно точки
Симметрия. Симметрия относительно точки Регрессия. Регрессионная статистика
Регрессия. Регрессионная статистика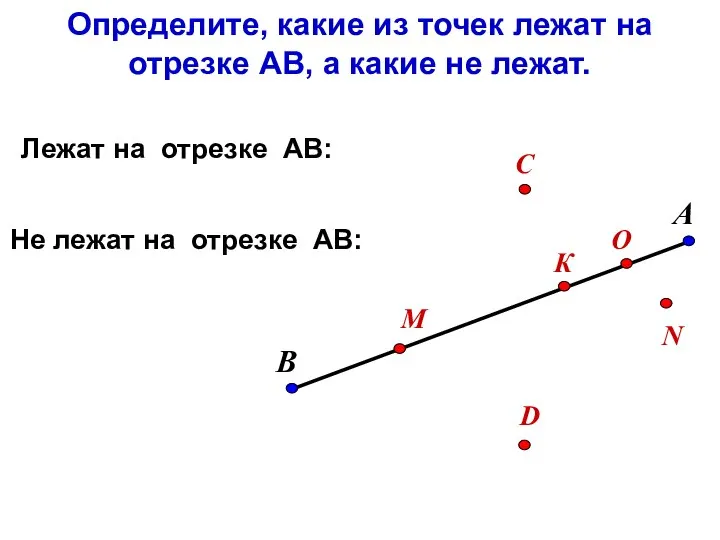 Отрезок. Длина отрезка
Отрезок. Длина отрезка Геометрия вокруг нас
Геометрия вокруг нас Уравнение. Решение задач с помощью уравнений
Уравнение. Решение задач с помощью уравнений Считаем со Смешариками (1 класс)
Считаем со Смешариками (1 класс) Луч – это отрезок. Ломаная состоит из звеньев
Луч – это отрезок. Ломаная состоит из звеньев Аналитическая геометрия
Аналитическая геометрия Презентация на тему Треугольники. Третий признак равенства
Презентация на тему Треугольники. Третий признак равенства  Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Последовательности и прогрессии (ПР №25)
Последовательности и прогрессии (ПР №25) Найди лишний пример
Найди лишний пример Уравнения фигур
Уравнения фигур Математика. Билет 5
Математика. Билет 5