Содержание
- 2. Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и
- 3. В развитии теории вероятностей весьма большую роль играли задачи, связанные с азартными играми, в первую очередь
- 4. Возникновение теории вероятностей в современном смысле слова относится к середине XVII века и связано с исследованиями
- 5. Крупный шаг вперед в развитии теории вероятностей связан с работами Якова Бернулли (1654-1705). Ему принадлежит первое
- 7. СЛУЧАЙНОЕ - НЕВОЗМОЖНОЕ - РАВНОВОЗМОЖНЫЕ - ДОСТОВЕРНОЕ - событие, которое может произойти, а может и не
- 8. Вероятностью события А называется отношение числа благоприятных исходов для события А к числу всех равновозможных исходов.
- 9. Пример. Андрей, Роман, Максим и Сергей бросили жребий, кому быть вратарем. Найти вероятность того, что вратарем
- 10. Свойства вероятности Вероятность достоверного события А равна единице: Р(А) =1 Вероятность невозможного события А равна нулю:
- 11. Задание B10 (№ 283483) В чемпионате по гимнастике участвуют 64 спортсменки: 20 из Японии, 28 из
- 12. Задание B10 (№ 283473) В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел
- 13. Игральный кубик бросили один раз. Какова вероятность того, что выпадает не менее 4 очков? Решение: Бросаем
- 14. Специальная формула вероятности, адаптированная для решении задач с монетами Пусть монету бросают n раз. Тогда вероятность
- 15. Задача. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни
- 16. Задание B10 (№ 283441) В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в
- 18. Два случайных события называются НЕСОВМЕСТИМЫМИ, если они могут произойти одновременно при одном и том же исходе
- 19. Задание B10 (№ 320385) На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов.
- 20. Событие В называется НЕЗАВИСИМЫМ от события А, если появления события А не изменяет вероятности события В.
- 21. Задание B10 (№ 320477) Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном
- 24. Скачать презентацию




















 В сказочной стране Дизайн
В сказочной стране Дизайн Текстовые задачи школьного ОГЭ Движение по воде
Текстовые задачи школьного ОГЭ Движение по воде Математический КВН
Математический КВН Математический анализ. Лекция 2
Математический анализ. Лекция 2 Пифагор и его школа
Пифагор и его школа Доли. 3 класс
Доли. 3 класс Сумма углов треугольника
Сумма углов треугольника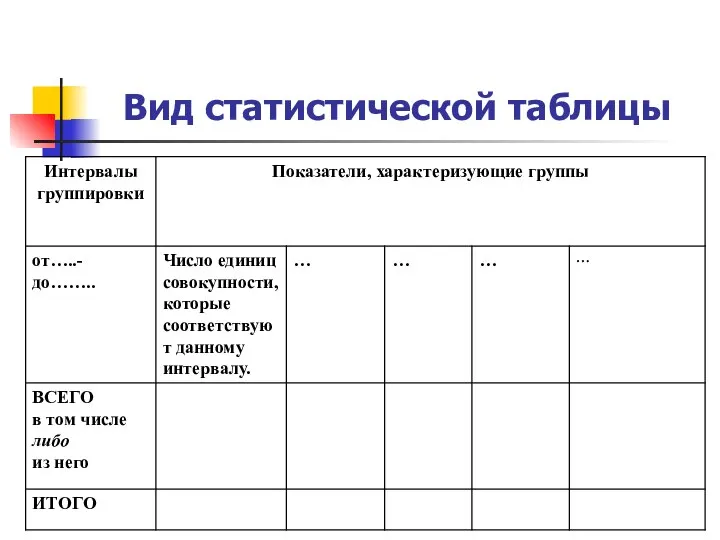 Вид статистической таблицы
Вид статистической таблицы Тригонометрические функции тангенс и котангенс
Тригонометрические функции тангенс и котангенс Наименьшее и наибольшее значение функции. Задачи
Наименьшее и наибольшее значение функции. Задачи Делимость целых чисел
Делимость целых чисел Связность графов. Маршруты, цепи, циклы
Связность графов. Маршруты, цепи, циклы Машинная арифметика в рациональных числах. Интервальные вычисления. Лекция 12
Машинная арифметика в рациональных числах. Интервальные вычисления. Лекция 12 Геометрические тела. 5 класс
Геометрические тела. 5 класс Понятие о задачах математической статистики
Понятие о задачах математической статистики Действие с дробями. Устная работа
Действие с дробями. Устная работа Сравнение чисел. 1 класс
Сравнение чисел. 1 класс Приближенные решения уравнений
Приближенные решения уравнений Состав числа 10
Состав числа 10 Число 6
Число 6 Презентация на тему КВН. Математика повсюду
Презентация на тему КВН. Математика повсюду  Графический способ решения систем уравнений. Свойства графиков функций
Графический способ решения систем уравнений. Свойства графиков функций Презентация на тему Части сферы и шара
Презентация на тему Части сферы и шара  Математика в астрономии и астрономия в математике Б.Б.Эскин Санкт-Петербургский государственный университет
Математика в астрономии и астрономия в математике Б.Б.Эскин Санкт-Петербургский государственный университет Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Второй признак равенства треугольников. 7 класс
Второй признак равенства треугольников. 7 класс Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений методом Гаусса Презентация на тему Место числового множителя в выражении с переменной
Презентация на тему Место числового множителя в выражении с переменной