Линейное программирование. (Лекция 1)

1.Общая задача линейного программирования
Дана система m линейных уравнений и неравенств с n переменными
…………………………………………..
…………………………………………..
и линейная функция

Необходимо найти такое решение системы
при котором линейная функция принимает оптимальное (т.е. максимальное или минимальное) значение .
Оптимальное решение иногда называют оптимальным планом (экономическая интерпретация).
Рассматривают различные формы задач линейного программирования.
Если все переменные неотрицательны и система ограничений состоит лишь из одних неравенств, то задача называется стандартной.
Если система ограничений состоит из одних уравнений, то задача называется канонической.
Любая задача линейного программирования может быть сведена к канонической, стандартной или общей задаче.

2. Система m линейных уравнений с n переменными,
основные (базисные) и неосновные (свободные) переменные). Базисные решения.
Рассмотрим систему
………..……………………………………………
Будем считать, что в системе (1.1) все m уравнений линейно независимы, т.е. r = m (r - ранг системы) и m < n .
Определение. Любые m переменных системы (1.1) называются основными (или базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n - m переменных называются неосновными (или свободными).
Замечание. Максимально возможное число групп основных переменных не превосходит числа всех сочетаний из n по m
(1.1)

Теорема. Если для системы m линейных уравнений с n переменными (1.1 ) существует хотя бы одна группа базисных переменных, то эта система является неопределенной, причем каждому произвольному набору значений cвободных переменных соответствует одно решение системы.
Д. Пусть x1,x2,…,xm - базисные переменные. Запишем систему уравнений в виде
………………………………………………………………
При произвольном наборе значений переменных xm+1 ,xm+2,…,xn получаем систему

…………………………………….
Определитель этой системы
по теореме Крамера система имеет единственное решение. В силу произвольного выбора свободных переменных получаем бесконечное множество решений.

Решение системы (1.1) называется допустимым, если оно содержит только неотрицательные компоненты.
Базисным решением системы m уравнений с n переменными называется решение, в котором все n - m свободных переменных равны нулю.
Базисное решение, в котором хотя бы одна из основных переменных равна нулю, называется вырожденным.
Пример. Найти все базисные решения системы уравнений
максимальное число пар базисных переменных
1) x1,x2 -,базисные переменные; x3, x4 – свободные переменные
2) x1,x3 - базисные переменные; x2, x4 – свободные переменные
базисное допустимое решение
x1, x2 не могут быть базисными переменными

3) x1,x4 - базисные переменные; x2, x3 – свободные переменные
4) x2 ,x3 - базисные переменные; x1, x4 – свободные переменные
5) x2,x4 - базисные переменные; x1, x3 – свободные переменные
6) x3,x4 - базисные переменные; x1, x2 – свободные переменные

3. Геометрический смысл решений линейных неравенств и их систем.
Теорема. Решением линейного неравенства
является одна из двух полуплоскостей, на которые прямая
делит всю плоскость, а также и сама прямая. Вторая полуплоскость вместе с прямой является решением неравенства

Доказательство
(предполагаем, что b>0)

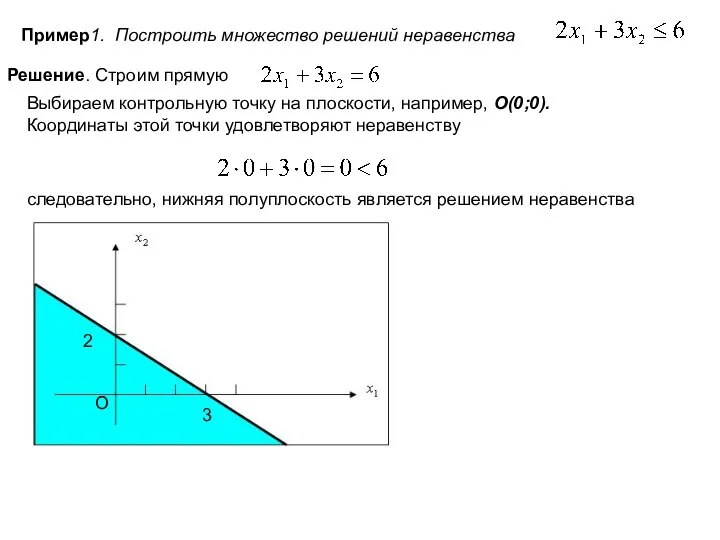
Пример1. Построить множество решений неравенства
Решение. Строим прямую
Выбираем контрольную точку на плоскости, например, O(0;0). Координаты этой точки удовлетворяют неравенству
следовательно, нижняя полуплоскость является решением неравенства
O
3
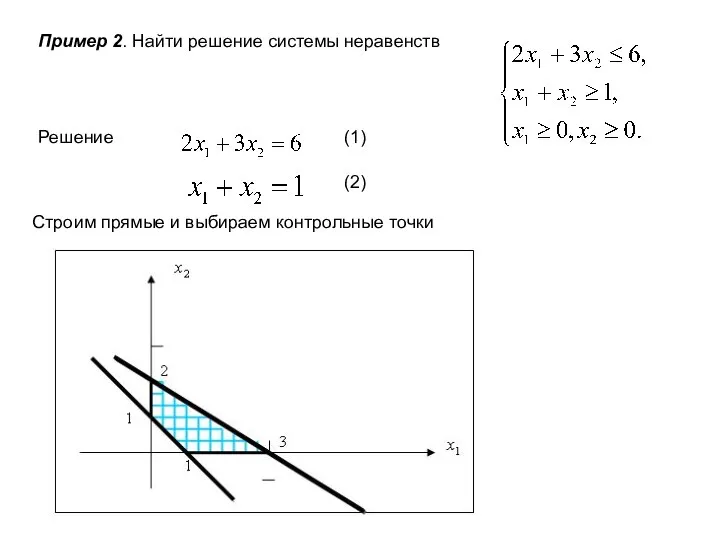
2

Пример 2. Найти решение системы неравенств
Решение
(1)
(2)
Строим прямые и выбираем контрольные точки