Содержание
- 2. Де зустрічаються Піраміди?
- 3. Найвідоміші Піраміди Світу
- 4. Означення Піраміди. Пірамідою називається многогранник, одна грань якого довільний многокутник (основа піраміди), а решта граней являють
- 5. Бічна поверхня піраміди Трикутники що об'єднані спільною точкою (вершиною піраміди) називаються БІЧНОЮ ПОВЕРХНЕЮ ПІРАМІДИ. А один
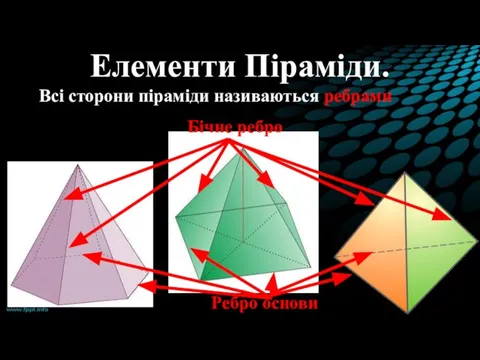
- 6. Елементи Піраміди. Всі сторони піраміди називаються ребрами Бічне ребро Ребро основи
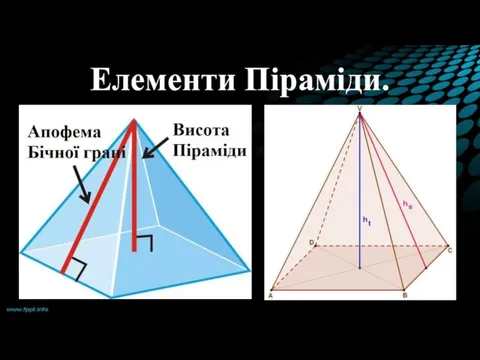
- 7. Елементи Піраміди.
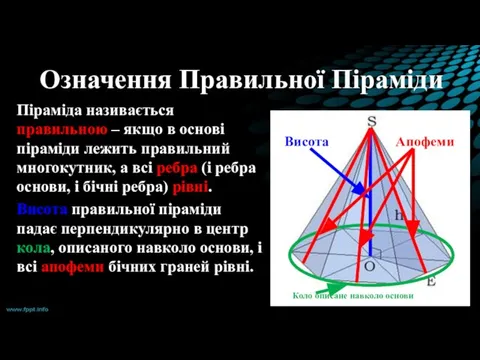
- 8. Означення Правильної Піраміди Піраміда називається правильною – якщо в основі піраміди лежить правильний многокутник, а всі
- 9. Правильні Піраміди
- 10. Площа Основи Правильної Піраміди В залежності від різновиду піраміди обчислюється за відповідними формулами: Трикутник Чотирикутник Шестикутник
- 11. Площа Бічної Поверхні Піраміди Площа бічної поверхні піраміди дорівнює добутку півпериметра її площі основи на довжину
- 12. Площа Повної Поверхні Піраміди Щоб знайти площу повної поверхні піраміди необхідно, до площі бічної поверхні піраміди
- 13. Площини Перерізу Піраміди Існує 3 види площин перерізу піраміди: Площина, яка паралельно до площини основи піраміди;
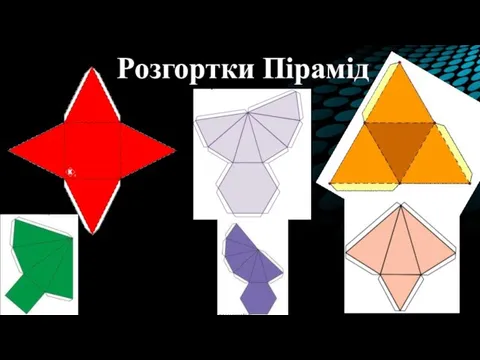
- 14. Розгортки Пірамід
- 15. Піраміди в грошах
- 16. Використання пірамід з метою оздоровлення
- 17. Жіночі фігури!!!
- 18. Піраміди на прапорах
- 19. Відома піраміда Хеопса в Єгипті – правильна чотирикутна піраміда, висота якої дорівнює 147м, а площа основи
- 20. Тест «Перевір себе…» ❶ Яке найменше число граней може бути у піраміди? а) 2 б) 3
- 22. Скачать презентацию















 Комплексные числа и действия над ними
Комплексные числа и действия над ними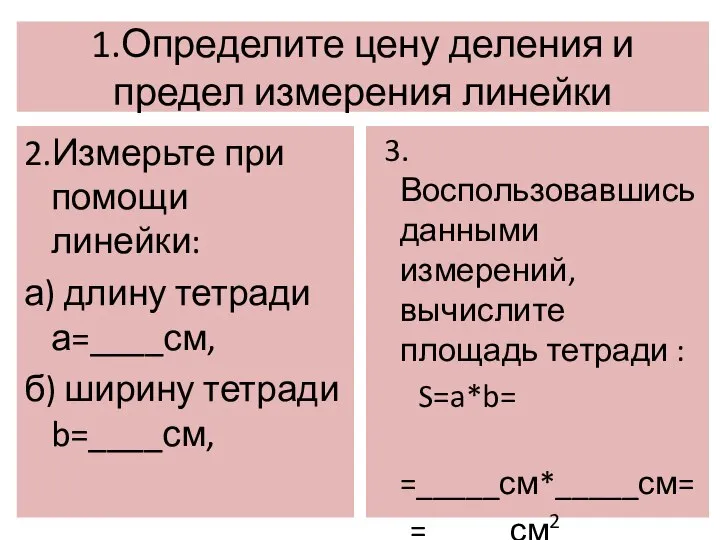 Цена деления и предел измерения линейки
Цена деления и предел измерения линейки Состав чисел
Состав чисел Умножение десятичных дробей. Графический диктант
Умножение десятичных дробей. Графический диктант Властивості і графіки тригонометричних функцій. Графік тангенса та котангенса числового аргументу
Властивості і графіки тригонометричних функцій. Графік тангенса та котангенса числового аргументу Реши уравнения
Реши уравнения Числоа 6, 7. Письмо цифры 6
Числоа 6, 7. Письмо цифры 6 Треугольники
Треугольники Теорема Виета. Урок систематизации, обобщения и контроля знаний
Теорема Виета. Урок систематизации, обобщения и контроля знаний Презентация на тему Метод интервалов
Презентация на тему Метод интервалов  Решение уравнений с одной переменной
Решение уравнений с одной переменной Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений Признаки параллельности прямых
Признаки параллельности прямых Умножение и деление отрицательных чисел. Урок-путешествие
Умножение и деление отрицательных чисел. Урок-путешествие Преобразование графиков вида у=f(х±а)
Преобразование графиков вида у=f(х±а) Математика. Числа до 20
Математика. Числа до 20 Какой функции соответствует график
Какой функции соответствует график Контрольная работа
Контрольная работа Теория антагонистических игр. Задачи для выполнения
Теория антагонистических игр. Задачи для выполнения Интерактивный тренажёр Весёлый счёт. Математика 1 класс
Интерактивный тренажёр Весёлый счёт. Математика 1 класс Задачи на перебор вариантов
Задачи на перебор вариантов Решение тригонометрических уравнений
Решение тригонометрических уравнений Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Дифференциальные уравнения высшего порядка
Дифференциальные уравнения высшего порядка Итогово-обобщающий урок. Площадь. Теорема Пифагора
Итогово-обобщающий урок. Площадь. Теорема Пифагора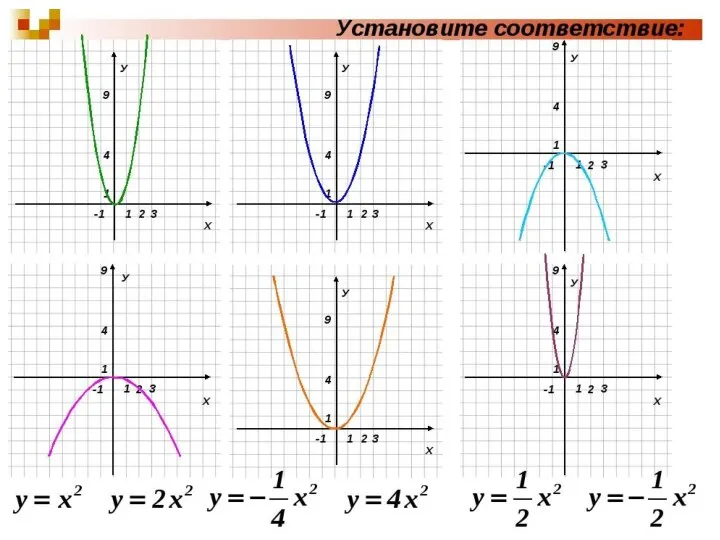 Графики функций
Графики функций Результант. Литература
Результант. Литература Занятие 45. Формулы двойного угла. Формулы половинного угла
Занятие 45. Формулы двойного угла. Формулы половинного угла