Содержание
- 2. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- 3. Лекция 7
- 4. Повторение испытаний
- 5. Определение сложного эксперимента Рассмотрим единичный эксперимент, в результате которого может произойти некоторое событие А. Если событие
- 6. Основные вопросы 1. Вероятность для некоторого числа появлений события А; 2. Вероятность для числа проведенных испытаний
- 7. Типы испытаний 1. Вероятность успеха постоянна в каждом испытании; 2. Вероятность успеха меняется.
- 8. Схема Бернулли (биномиальная) Пусть производится n независимых испытаний. Пусть P(А)=p в каждом испытании и q =
- 9. Найти ={в n испытаниях событие А наступит k раз}
- 10. Вероятность события {в n испытаниях А наступит k раз и не наступит n – k раз}
- 11. Число таких событий равно Так как эти события несовместны и равновероятны, получаем Полученную формулу называют формулой
- 12. Пример 1 Университетом для студенческих общежитий приобретено 5 телевизоров. Для каждого из них вероятность выхода из
- 13. Решение Из условия задачи выпишем p, n, k, q. n=5; k=1; p=0,1; q=0,9. Тогда по формуле
- 14. Вероятность того, что расход электроэнергии в продолжении одних суток не превысит установленной нормы, равна р =
- 15. Решение р = 0,75. q = 1 – p = 1 – 0,75 = 0,25. Искомая
- 16. Схема Пуассона Пусть вероятность успеха при фиксированном числе испытаний n постоянна и мала, уменьшается с ростом
- 17. Формула Пуассона
- 18. Пример 1 Вероятность того, что какой-нибудь абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная
- 19. Решение По условию задачи p=0,01; n=300; k=4. Найдем λ=300⋅0,01=3 По формуле Пуассона
- 20. Пример 2 Найти вероятность не более двух успехов в схеме Пуассона при
- 21. Решение
- 22. Геометрическая схема Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р
- 23. Основной вопрос Пусть в первых k – 1 испытаниях событие А не наступило, а в k-м
- 24. Пример Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р =
- 25. Решение Из условия задачи выпишем р = 0,6; q = 0,4; k = 3.
- 26. Пользоваться формулой Бернулли при больших значениях n достаточно трудно. Например, если n=5000, k=3000,p=0,1, то для отыскания
- 27. Теорема Пуассона Пусть в схеме Бернулли n велико, p мало и npq
- 28. Пример Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна
- 30. Скачать презентацию



























 Геометрия, 10 класс
Геометрия, 10 класс Параллельные алгоритмы вычислительной алгебры. Распараллеливание на компьютерах с распределенной памятью
Параллельные алгоритмы вычислительной алгебры. Распараллеливание на компьютерах с распределенной памятью 1665470218901_Лекция Бернулли-1
1665470218901_Лекция Бернулли-1 Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами
Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами Задачи на нахождение элементов призмы
Задачи на нахождение элементов призмы Сложение однозначных чисел с переходом через десяток вида * + 6
Сложение однозначных чисел с переходом через десяток вида * + 6 Треугольник. Свойства прямоугольного треугольника
Треугольник. Свойства прямоугольного треугольника Площадь многоугольников
Площадь многоугольников Презентация на тему Космическое путешествие 1 класс
Презентация на тему Космическое путешествие 1 класс  Комбинаторная задача с лампочками
Комбинаторная задача с лампочками Математическая интеллектуальная игра для всей семьи
Математическая интеллектуальная игра для всей семьи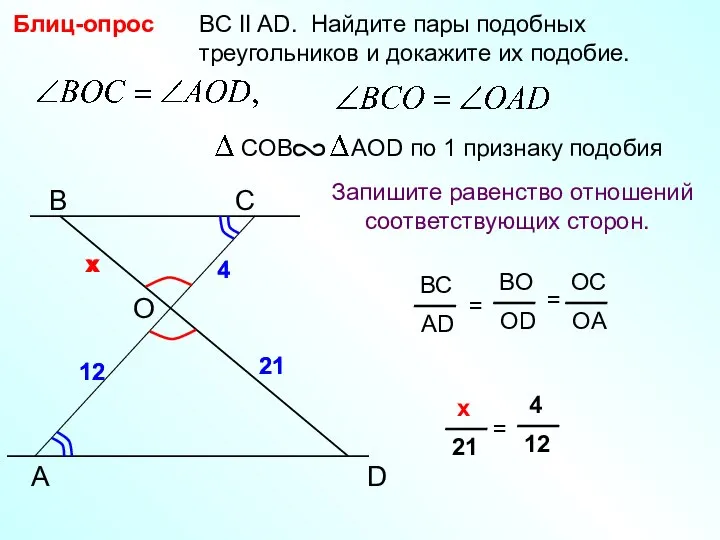 Признаки подобия треугольников
Признаки подобия треугольников Веселая математика!
Веселая математика! О треугольниках
О треугольниках Методы решения системы трёх линейных уравнений с тремя неизвестными
Методы решения системы трёх линейных уравнений с тремя неизвестными Презентация на тему Деловая игра по математике
Презентация на тему Деловая игра по математике  Презентация на тему Комбинаторные задачи (5 класс)
Презентация на тему Комбинаторные задачи (5 класс)  Тригонометрические уравнения
Тригонометрические уравнения Формулы сокращённого умножения
Формулы сокращённого умножения Длина окружности
Длина окружности Пирамида
Пирамида Понятие логарифма
Понятие логарифма Співвідношення між тригонометричними функціями
Співвідношення між тригонометричними функціями Задачи на пропорцию
Задачи на пропорцию Подготовка к ЕГЭ по математике
Подготовка к ЕГЭ по математике Задания по таблицам
Задания по таблицам Выражение отношения в процентах
Выражение отношения в процентах Числовая окружность. Занятие 1-2
Числовая окружность. Занятие 1-2