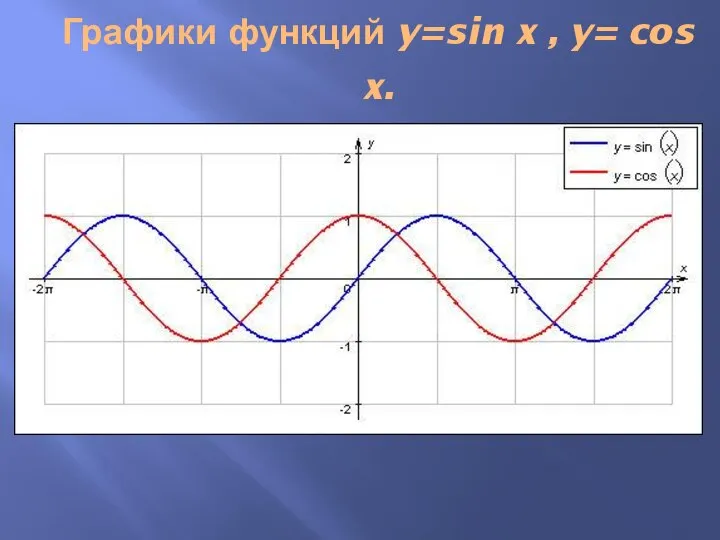
Слайд 3Графики функций y=sin x , y= cos x.
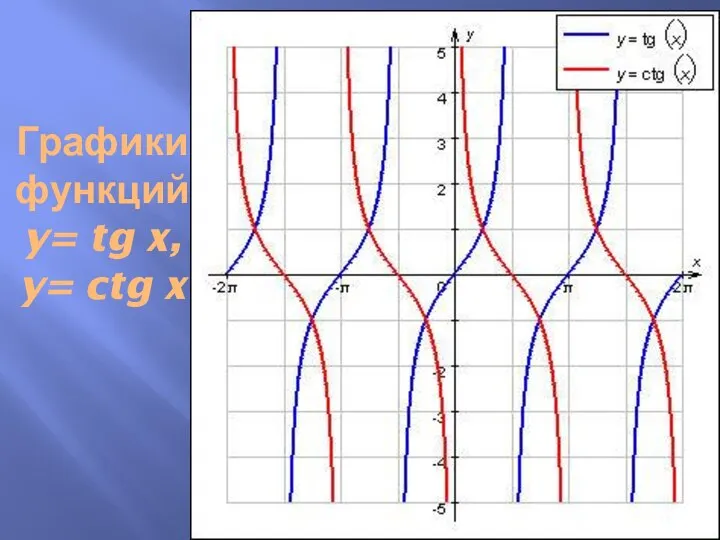
Слайд 4Графики
функций
y= tg x,
y= ctg x
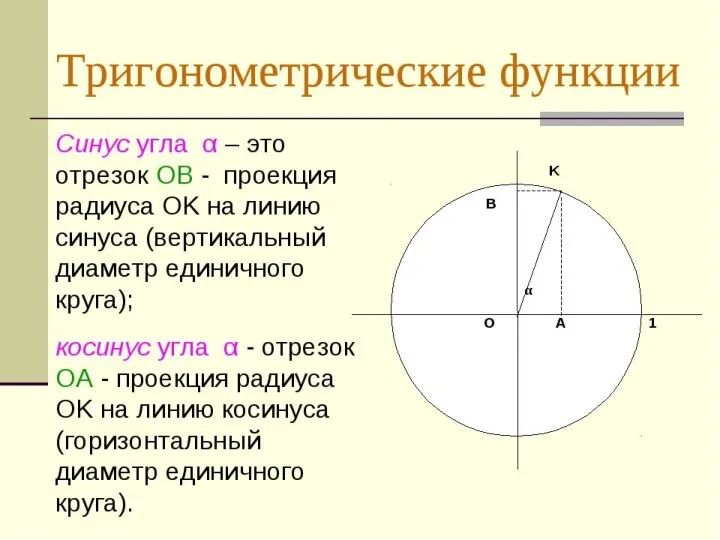
Слайд 5Свойства функций:
y=sin x , y= cos x , y= tg x

, y= ctg x .
Слайд 6Область определения функций
y=sin x , y= cos x х – любое число,
y=

tg x х – любое число, кроме x=/2+ n,
y= ctg x х – любое число, кроме x=n.
Слайд 7Множество значений функции
y=sin x , y= cos x [-1;1]
y= tg x ,
![Множество значений функции y=sin x , y= cos x [-1;1] y= tg](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1040105/slide-6.jpg)
y= ctg x Любое значение
Слайд 8Чётность и нечётность:
Нечетные функции
sin (–х) = –sin х
tg (–х) = –tg х

ctg (–х) = –ctg х
Четные функции
cos (–х) = cos х
Слайд 9Периодичность функций
Период T=2
sin (х + 2 ) = sin х
cos(х

+ 2 ) = cos х
Период T=
tg(х + ) = tg х,
ctg(х + ) = ctg х,
Слайд 10Применение
Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела.
Большое

значение имеет техника триангуляции, позволяющая измерять расстояния до недалеких звезд в астрономии, между ориентирами в географии, контролировать системы навигации спутников.




![Множество значений функции y=sin x , y= cos x [-1;1] y= tg](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1040105/slide-6.jpg)



 Презентация на тему Округление натуральных чисел
Презентация на тему Округление натуральных чисел  Своя игра. Алгоритмы
Своя игра. Алгоритмы Симметрия в пространстве
Симметрия в пространстве Сложение и вычитание в пределах 10
Сложение и вычитание в пределах 10 Понятие многогранника
Понятие многогранника Формирование математических представлений у детей 4-5 лет
Формирование математических представлений у детей 4-5 лет Задачи на готовых чертежах по теме Подобие
Задачи на готовых чертежах по теме Подобие Терема Пифагора
Терема Пифагора Случаи вычитания 12 -
Случаи вычитания 12 - Значение логического выражения (тема № 3)
Значение логического выражения (тема № 3) Линейные пространства и линейные операторы. Лекция 5
Линейные пространства и линейные операторы. Лекция 5 Проценты. Задания
Проценты. Задания Парная регрессия: линейный анализ
Парная регрессия: линейный анализ Подготовка к к/р
Подготовка к к/р Путешествие в мир обыкновенных
Путешествие в мир обыкновенных Цифра 2
Цифра 2 Путешествие в Изумрудный город
Путешествие в Изумрудный город Односторонние пределы
Односторонние пределы Законы алгебры логики. Задания
Законы алгебры логики. Задания Презентация на тему Геометрия в жизни Многогранники 6 класс
Презентация на тему Геометрия в жизни Многогранники 6 класс  Степенные, показательные, логарифмические и тригонометрические функции
Степенные, показательные, логарифмические и тригонометрические функции Статистические сравнения
Статистические сравнения Расстояния. Подготовка к ЕГЭ по математике 2019
Расстояния. Подготовка к ЕГЭ по математике 2019 Квадратный корень. Контрольная работа, задания
Квадратный корень. Контрольная работа, задания Определение производной. Физический смысл производной. Приращение аргумента и приращение функции
Определение производной. Физический смысл производной. Приращение аргумента и приращение функции Повторение. Урок для 8 класса
Повторение. Урок для 8 класса النشاط الثالث
النشاط الثالث Геометрические фигуры
Геометрические фигуры