Теория вероятности

Теорией вероятности называется раздел математики, изучающий закономерности и шансы наступления интересующего события.

Известно, по крайней мере, шесть основных схем определения и понимания вероятности. Не все они в равной мере используются на практике и в теории, но, тем не менее, все они имеют за собой разработанную логическую базу и имеют право на существование.
Понятие вероятности

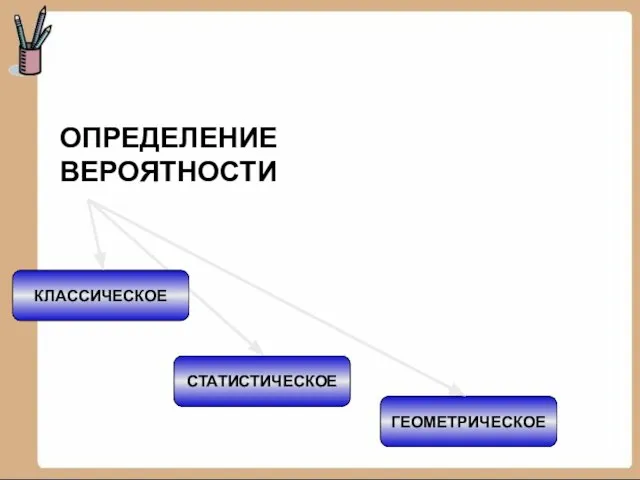
КЛАССИЧЕСКОЕ
СТАТИСТИЧЕСКОЕ
ГЕОМЕТРИЧЕСКОЕ
ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

Вероятностью Р наступления случайного события А называется отношение , где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов:
КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.

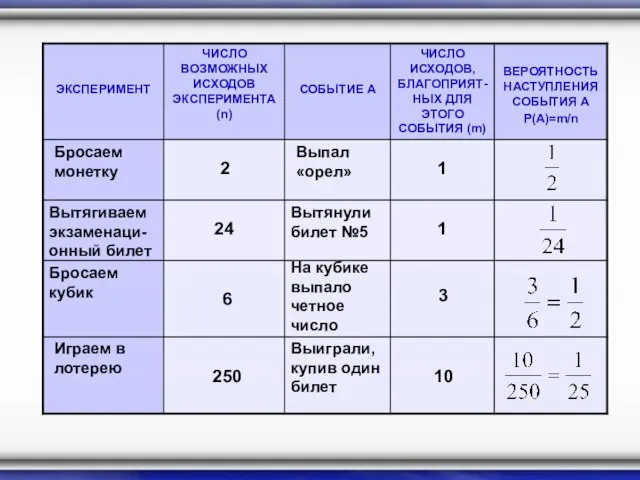
Бросаем монетку
2
Выпал «орел»
1
Вытягиваем экзаменаци- онный билет
Вытянули билет №5
24
1
Бросаем кубик
На кубике выпало четное число
6
3
Играем в лотерею
Выиграли, купив один билет
250
10

Вероятность достоверного события равна
Вероятность невозможного события равна
Вероятность события А не меньше , но не больше
?
1
?
?
?
0
1
0

На 100 электрических лампочек в среднем приходится 4 бракованных. Какова вероятность, что взятая наугад лампочка окажется исправной?
На 400 компакт-дисков в среднем приходится 8 бракованных. Какова вероятность, что взятый наугад компакт-диск окажется исправным?
17 точек из 50 покрашены в синий цвет, а 13 точек из оставшихся покрашены в оранжевый цвет. Какова вероятность того, что случайно выбранная точка окажется окрашенной?
Из слова «математика» случайным образом выбирается одна буква. Какова вероятность, что выбранная буква встречается в этом слове только 1 раз?
Из слова «аттестация» случайным образом выбирается одна буква. Какова вероятность, что выбранная буква окажется буквой «а»?

Случайная величина (СВ) – это величина, которая в результате опыта может принимать те или иные значения, причем до опыта мы не можем сказать, какое именно значение она примет.
Случайные величины обозначаются буквами латинского алфавита X, Y, Z.
Случайные величины могут быть трех типов:
дискретные,
непрерывные,
смешанные (дискретно-непрерывные).

Дискретная случайная величина (ДСВ) может принимать конечное или бесконечное счетное число значений. Например, подбрасываем монету 5 раз. Случайная величина X- число появлений герба: 0,1,2,3,4,5.
Пусть X - дискретная случайная величина, которая принимает значения: x1, x2, ..., хn... с некоторой вероятностью pi ,где i = 1,2,..., n,... Тогда можно говорить о вероятности того, что случайная величина X приняла значение хi: pi = P(X = xi).

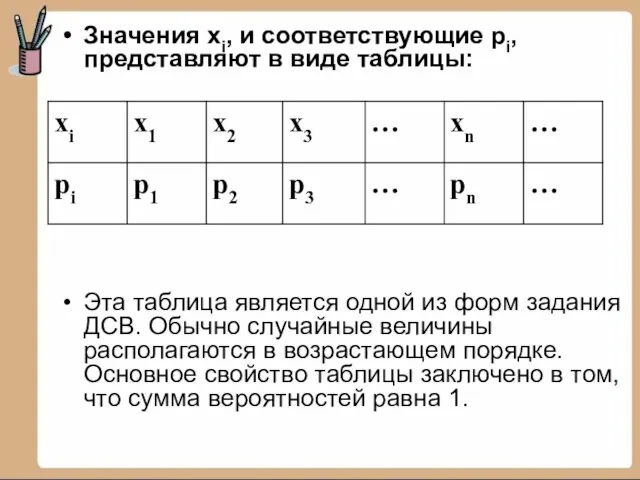
Значения хi, и соответствующие рi, представляют в виде таблицы:
Эта таблица является одной из форм задания ДСВ. Обычно случайные величины располагаются в возрастающем порядке. Основное свойство таблицы заключено в том, что сумма вероятностей равна 1.

Математическим ожиданием дискретной случайной величины называется число, равное сумме произведений всех значений случайной величины на вероятности этих значений.
Если случайная величина Х принимает значения x1, x2, ... , xn с вероятностями соответственно p1, p2,... pn , то математическое ожидание находится по формуле:
М(x) = x1p1+ x2p2 + ... + xnpn
Математическое ожидание иначе называют средним значением случайной величины, так как оно указывает некоторое среднее число, около которого группируются все значения случайной величины.

Дисперсией дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания: D(x) = M(x2) – (M(x))2 . Дисперсия случайной величины характеризует степень разброса значений случайной величины относительно её математического ожидания.
Средним квадратичным отклонением дискретной случайной величины называется квадратный корень из дисперсии:

Найти числовые характеристики случайной величины Х, имеющей закон распределения, представленный в таблице
Найдём математическое ожидание.
M(x) = –2 . 0,3 + (–1) . 0,1 + 1 . 0,2 + 2 . 0,1 + 3 . 0,3= =0,6