predel-posledovatelnosti-svoystva-i

а) 1, 2, 3,…,n,….
б) 1, -1/2, 1/3, -1/4,…,
в) sin 1, sin 2, sin 3,…, sin n,…
Любое число в совокупности имеет номер
в соответствии с тем местом, которое оно
занимает и от него зависит.
Пример: n=12
а) a12=12
б) b12=-1/12
в) c12=sin 12

ОПР. Совокупность чисел, каждое
из которых имеет свой номер n є N
и от него зависит, называется
числовой последовательностью.
Xn ={X1,X2,…,Xn}
an={a1,a2,…,an}

Задать числовую последовательность, значит указать как отыскивается любой ее член, если известен номер занимаемого им места.
Описание
(xn )-последовательность приближенных значений √2 с недостатком с точностью до 0,1; 0,01; 0,001…
√2=1,1421356…
(Xn)={1,1; 1,14; 1,142; 1,1421;…}

2. Формула n-го члена.
Формула, позволяющая найти любой член последовательности по его номеру
Назовите первые 5 членов последовательности (Xn)= n²

Понятие сходящейся последовательности
Рассмотрим две числовые последовательности (уn) и (хn) и изобразим их члены точками на координатной прямой.
(уn): 1, 3, 5, 7, 9,…, 2n – 1,…;
(хn):
у
0
1
3
5
7
9
11
13
0
1
х
Обратим внимание, что члены последовательности (хn) как бы «сгущаются» около точки 0, а у последовательности (уn) такой точки нет. В подобных случаях говорят, что последовательность (хn) сходится, а последовательность (уn) расходится.

Понятие сходящейся последовательности
(уn): 1, 3, 5, 7,…,(2n-1),...
Нет точки сгущения
Последовательность
расходится
(хn): 1, 1/2, 1/3, 1/4, 1/6,…1/n,..
Точка сгущения – 0
Последовательность
сходится
Чтобы узнать является ли конкретная точка, взятая на прямой, «точкой сгущения» для членов заданной последовательности, введем следующее понятие.

Окрестность точки
Определение 1. Пусть а – точка прямой, а r – положительное число. Интервал (а - r; a + r) называют окрестностью точки а, а число r – радиусом окрестности.
Пример. (3,97; 4,03) – окрестность точки 4, радиус равен 0,03.
х
a-r
a+r
a

Предел последовательности
В математике «точку сгущения» для членов заданной последовательности принято называть «пределом последовательности».
Определение 2. Число b называют пределом последовательности (уn), если в любой заранее выбранной окрестности точки b содержатся все члены последовательности, начиная с некоторого номера.
Обозначение: 1. (уn стремится к b или уn сходится к b);
2. (предел последовательности уn при стремлении n
к бесконечности равен b)

Формулы
1) lim 1/n = 0
n→∞
2) lim qn = 0, если 0 < |q| < 1
n→∞
Если q > 1, то lim qn не существует.
n→∞
3) lim С = С
n→∞
4) lim (к /nm) = 0
n→∞

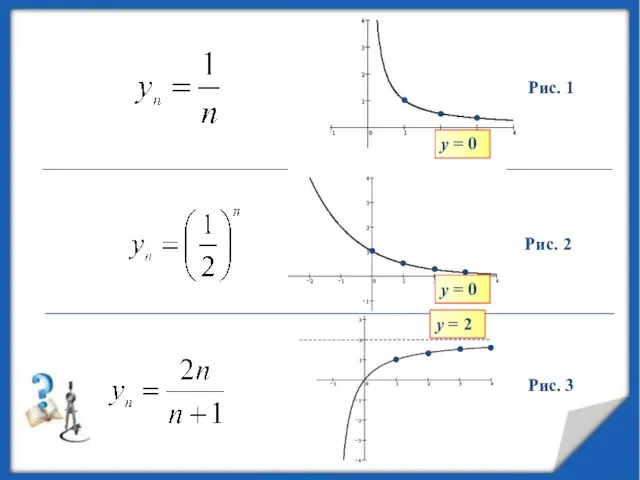
Предел последовательности
Построим графики последовательностей:

Рис. 1
Рис. 2
Рис. 3
у = 0
у = 0

Асимптоты графика
Обратите внимание, что на всех трех
рисунках точки графика, по мере их ухода
вправо, все ближе и ближе подходят к
некоторой горизонтальной прямой:
на рис 1 – к прямой у = 0,
на рис 2 – к прямой у = 0,
на рис 3 – к прямой у = 2.
Каждую из этих прямых называют
горизонтальной асимптотой графика.

Асимптоты графика
Вообще равенство
означает, что прямая у = а
является горизонтальной асимптотой
графика последовательности,
т.е. графика функции

Свойства
● Если последовательность сходится,
то только к одному пределу.
● Если последовательность сходится ,
то она ограничена.
Обратное−неверно:1,2,3,1,2,3,…−
ограниченная последовательность,
но она не сходится
●Теорема Вейерштрасса
Если последовательность монотонна
и ограничена, то она сходится.

Карл Теодор
Вейерштрасс-
выдающийся немецкий
математик, отец
«современного анализа»
1815-1897 г.
Кратер на Луне

Свойства вычисления пределов
Если lim хn = b и lim уn = c , то
n→∞ n→∞
1)Предел суммы равен сумме пределов:
lim (хn+ уn) = lim хn + lim уn = b + c
n→∞ n→∞ n→∞
2)Предел произведения равен произведению пределов:
lim (хn· уn) = lim хn ∙ lim уn = b · c
n→∞ n→∞ n→∞
3)Предел частного равен частному пределов:
lim (хn : уn) = lim хn : lim уn = b : c
n→∞ n→∞ n→∞
4)Постоянный множитель можно вынести за знак предела:
lim (k · хn) = k · lim хn = k ∙ b
n→∞ n→∞

Примеры вычисления пределов
Пример 1. Вычислить
Решение. Делим числитель и знаменатель
дроби почленно на наивысшую из имеющихся
степень переменной x, т.е. на x5.

Примеры вычисления пределов
Пример 2. Вычислить
Решение. Делим числитель и знаменатель
дроби почленно на наивысшую из имеющихся
степень переменной x т.е. на x4.

Примеры вычисления пределов
Пример 3. Вычислить
Решение. Делим числитель и знаменатель
дроби почленно на наивысшую из имеющихся
степень переменной x, т.е. на x6.
(не существует)

Правила вычисления пределов
1. Если старшая степень числителя и знаменателя совпадают, то предел такого вида всегда будет равен отношению коэффициентов при старших степенях переменной.

Правила вычисления пределов
2. Если степень знаменателя выше степени числителя, то предел такого вида равен нулю.

Правила вычисления пределов
3. Если же старшая степень числителя выше степени знаменателя, то, очевидно, все слагаемые знаменателя в пределе будут равны нулю, это означает, что предел не существует.

1.
2.
3.
4.
Вычислите самостоятельно пределы функций на бесконечности:

Методика вычисления пределов в точке
Если функция существует в точке x = a, то ее предел равен f(a).
Пример 1. Вычислить
Решение. Подставим вместо x число 3 (т.к. x?3) и применим правила вычисления пределов.
Примеры вычисления пределов

Пример 2. Вычислить
Решение.
Пример 3. Вычислить
Решение.
Примеры вычисления пределов

Методика вычисления пределов в точке
Если же функция в точке х = а не существует, в знаменателе дроби ноль, то вычисляем значение числителя в этой точке.
1.
2.
3.

Пример 1. Вычислить
Решение. Подставим вместо x число 2 (т.к. x?2) и применим правила вычисления пределов.
Примеры вычисления пределов

Пример 2. Вычислить
Решение. Подставим вместо x число 2 (т.к. x?2) и применим правила вычисления пределов.
Примеры вычисления пределов

Пример 3. Вычислить
Решение. Подставим вместо x число 3 (т.к. x?3) и применим правила вычисления пределов.
Примеры вычисления пределов

Методика вычисления пределов в точке

Примеры вычисления пределов
Пример 1. Вычислить
выяснили, что при х = 1 и числитель и знаменатель равны нулю, значит имеем неопределенность вида

Примеры вычисления пределов
Пример 2. Вычислить
выяснили, что при х = 1 и числитель и знаменатель равны нулю, значит имеем неопределенность вида

Примеры вычисления пределов
Пример 3. Вычислить
Активно используйте формулы сокращенного умножения

Следующие пределы вычислите самостоятельно
1. 2.
4.
6.
7. 8.