Тетраэдр

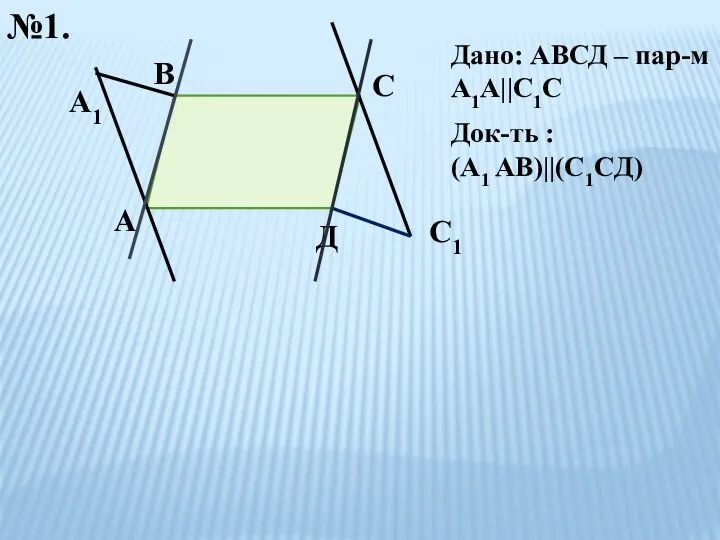
А
В
С
Д
А1
С1
Док-ть :
(А1 АВ)||(C1CД)
Дано: АВСД – пар-м
А1А||C1C
№1.

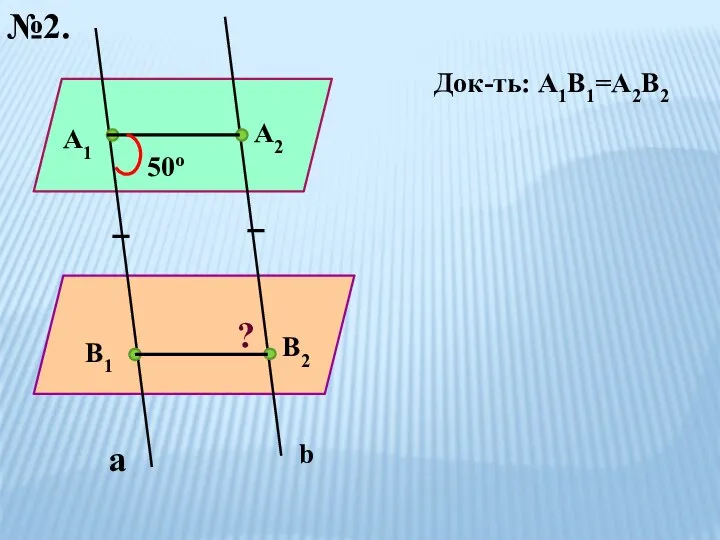
№2.
а
b
А1
В1
А2
В2
Док-ть: А1В1=А2В2
50о
?

Тетраэдр

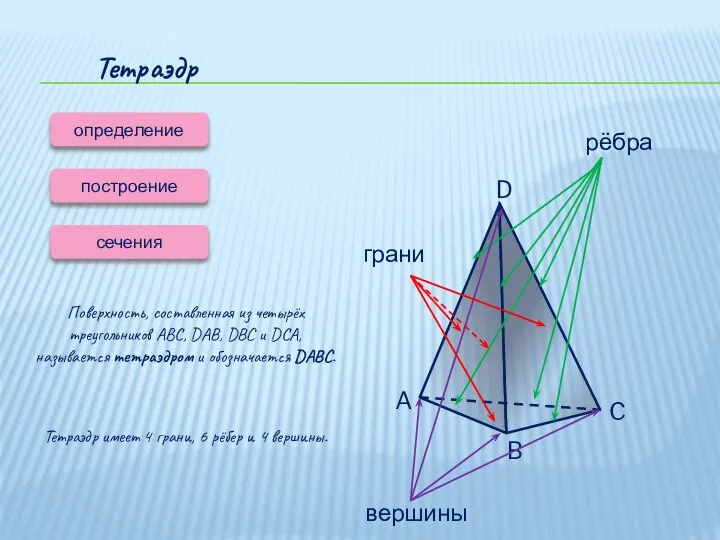
Тетраэдр
определение
сечения
Поверхность, составленная из четырёх треугольников ABC, DAB, DBC и DCA, называется тетраэдром и обозначается DABC.
D
A
B
C
грани
рёбра
вершины
Тетраэдр имеет 4 грани, 6 рёбер и 4 вершины.
построение

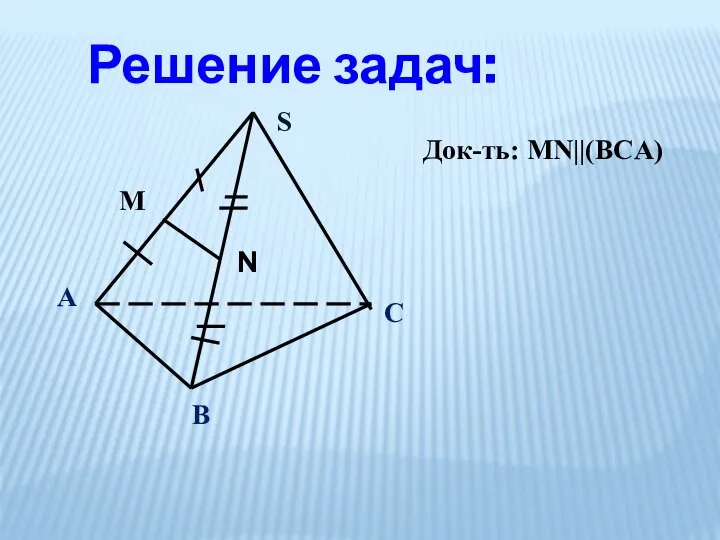
Решение задач:
А
В
С
S
M
N
Док-ть: MN||(BCA)

В классе: №69, №73
Дома: п.12, №67(а),
№70

тест

1. Если две плоскости имеют общую точку, то
А) они называются пересекающимися, Б) они пересекаются по прямой проходящей через эту точку,
В) они параллельны
2. Через прямую и не лежащую на ней точку
А) проходит плоскость и при том только одна
Б) проходит бесконечно много плоскостей
В) нельзя провести плоскость
3. Две прямые называются скрещивающимися, если
А) они лежат в одной плоскости и не пересекаются
Б) они не пересекаются
В) они не пересекаются и не параллельны
4. Если прямая пересекает две параллельные прямые, то
А) она пересекает плоскость, образованную этими параллельными прямыми
Б) она параллельна плоскости, образованными этими прямыми
В) она лежит в плоскости, определенными этими параллельными прямыми
5. Если две прямые параллельны третьей, то
А) они лежат в одной плоскости
Б) они параллельны
В) они скрещивающиеся