Содержание
- 2. Введение Ша́хматы — настольная логическая игра со специальными фигурами на 64-клеточной доске для двух соперников, сочетающая
- 3. История Считается, что история шахмат насчитывает не менее полутора тысяч лет. Известно множество версий, объясняющих развитие
- 4. Математика шахматной доски Согласно легенде индийский принц решил наградить изобретателя шахмат и предложил ему самому выбрать
- 5. Математика шахматной доски Магический квадрат порядка n представляет собой квадратную таблицу nXn, заполненную целыми числами от
- 6. Рассмотрим одну из старинных дебютных табий (начальных расположений фигур) под названием альмуджаннах. Она получается из современной
- 7. Геометрия шахматной доски Можно сказать, что ничего удивительного и интересного здесь нет. Можно подумать, что при
- 8. Геометрия шахматной доски Наиболее интересное свойство шахматной доски заключается в весьма необычном измерении расстояний на ней.
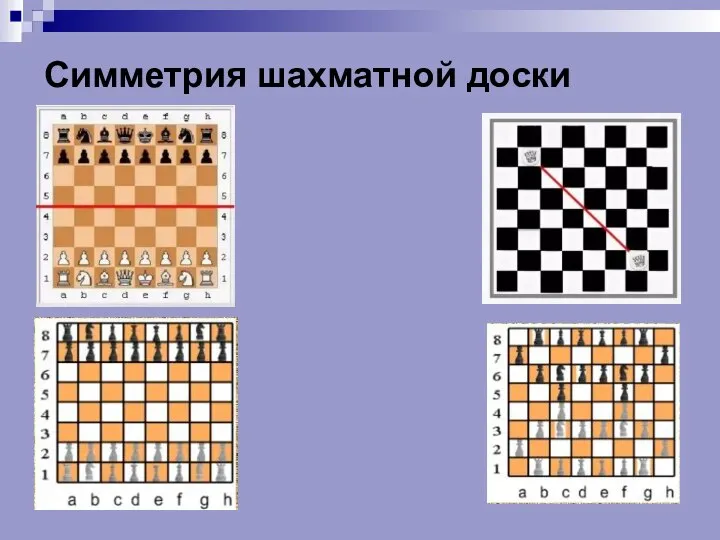
- 9. Симметрия шахматной доски На шахматной доске можно провести прямую, разделяющую левый и правый фланги доски (граница
- 10. Симметрия шахматной доски
- 11. Пятнадцать полей пересечены одной прямой Семь прямых пересекают все поля доски Сколько нужно провести разрезов на
- 12. Система координат Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте
- 13. Легенда о четырёх алмазахОдин восточный властелин был таким искусным игроком, что за всю жизнь потерпел всего
- 14. На какое максимальное число разных частей можно разрезать шахматную доску, если считать разными части, отличающиеся своей
- 15. Парадокс с разрезанием доски Разрежем доску на четыре части, как показано на рис. 5а, и составим
- 16. Можно ли целиком покрыть домино квадрат 8x8, из которого вырезаны противоположные угловые клетки? Задача о домино
- 17. Задача о домино Можно воспользоваться алгебраическими рассуждениями, однако «шахматное» решение проще. Окрасим урезанный квадрат в черно-белый
- 18. Математика шахматной доски Домино покрывают доску Пусть на шахматной доске вырезаны два поля разного цвета. Всегда
- 19. Задача об обходе конём всех клеток шахматной доски Требуется обойти ходом коня все клетки шахматной доски,
- 20. Математика шахматных фигур Математика шахматных фигур Математика шахматных фигур Каждая не занятая ладьёй клетка находится под
- 21. Шахматы справедливо считают единственной игрой из всех, придуманных человеком, в которой сочетаются спорт, искусство и наука.
- 23. Скачать презентацию



















 Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс Величины. Длина
Величины. Длина Случайные величины 14 сен
Случайные величины 14 сен Возникновение первых математических понятий
Возникновение первых математических понятий Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс
Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс Умножение на 1 и 0
Умножение на 1 и 0 Диктант по геометрии
Диктант по геометрии Выбор схемы измерения переменных
Выбор схемы измерения переменных Умножение на 10,100,1000, 0,1, 0,01, 0,001
Умножение на 10,100,1000, 0,1, 0,01, 0,001 Подготовка к блиц-турниру
Подготовка к блиц-турниру Скалярное прозведение векторов
Скалярное прозведение векторов Шифр Цезаря
Шифр Цезаря Сфера и шар
Сфера и шар Многогранники. Призма
Многогранники. Призма Пропорции и проценты
Пропорции и проценты Координаты суммы, разности и произведения вектора на число
Координаты суммы, разности и произведения вектора на число Графический диктант
Графический диктант Презентация на тему Расположение точек относительно осей координат
Презентация на тему Расположение точек относительно осей координат  Найдите высоту и медиану треугольника
Найдите высоту и медиану треугольника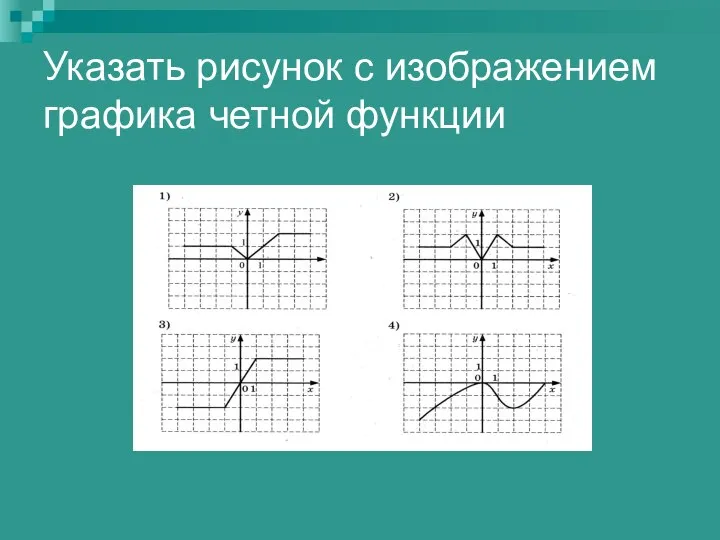 Указать рисунок с изображением графика четной функции
Указать рисунок с изображением графика четной функции Параллелепипед
Параллелепипед Выражение отношения в процентах
Выражение отношения в процентах Задачи на проценты. Схемы
Задачи на проценты. Схемы Решение нелинейных уравнений
Решение нелинейных уравнений Сложение с переходом через десяток. Тренажёр
Сложение с переходом через десяток. Тренажёр Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс
Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения
Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика