Содержание
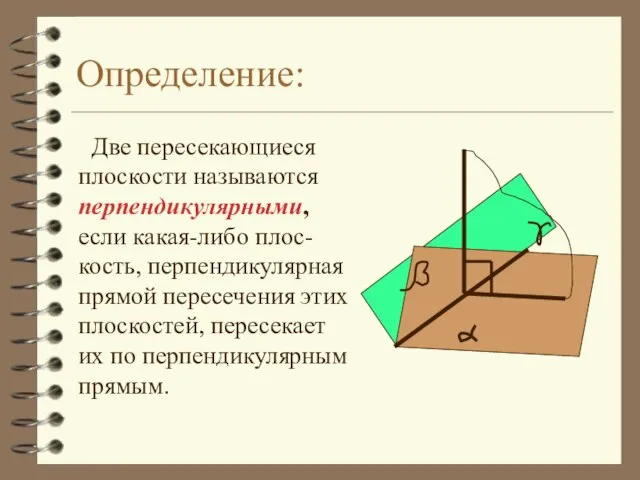
- 2. Определение: Две пересекающиеся плоскости называются перпендикулярными, если какая-либо плос-кость, перпендикулярная прямой пересечения этих плоскостей, пересекает их
- 3. Теорема Если плоскость проходит через прямую, перпендикуляр-ную другой плоскости, то эти плоскости перпендикулярны.
- 4. Работаем вместе! Рисунок Дано: ___________________ Доказать:
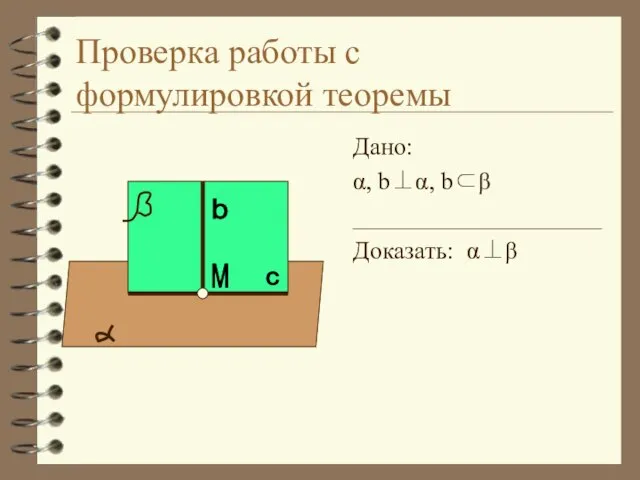
- 5. Проверка работы с формулировкой теоремы Дано: α, b⊥α, b⊂β ____________________ Доказать: α⊥β b c М
- 6. Работаем в группах!
- 7. Доказательство: Проведем в плоскости α через точку пересечения прямой b с плоскостью прямую а, перпендикулярную прямой
- 8. Затребованная помощь I Шаги: I. а) a ⊥ c, a ⊂ α, Μ ∈ a; б)
- 9. Затребованная помощь II Обоснование: I. а) Через каждую точку прямой на плоскости можно провести перпендикулярную ей
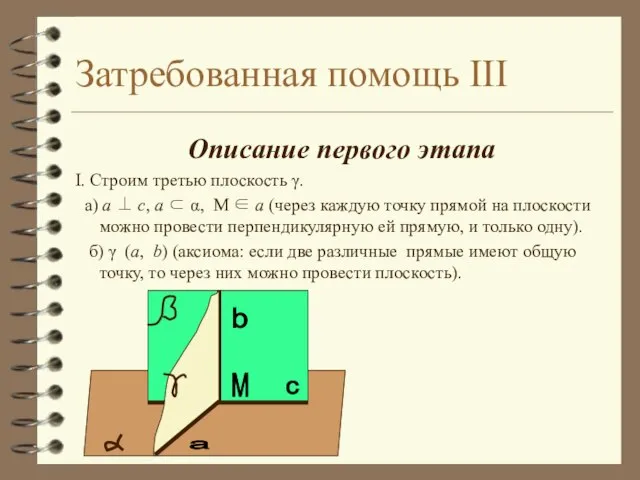
- 10. Затребованная помощь III Описание первого этапа I. Строим третью плоскость γ. а) a ⊥ c, a
- 11. Затребованная помощь IV Названия этапов: I. Строим третью плоскость γ. II. Доказываем, что γ удовлетворяет признакам,
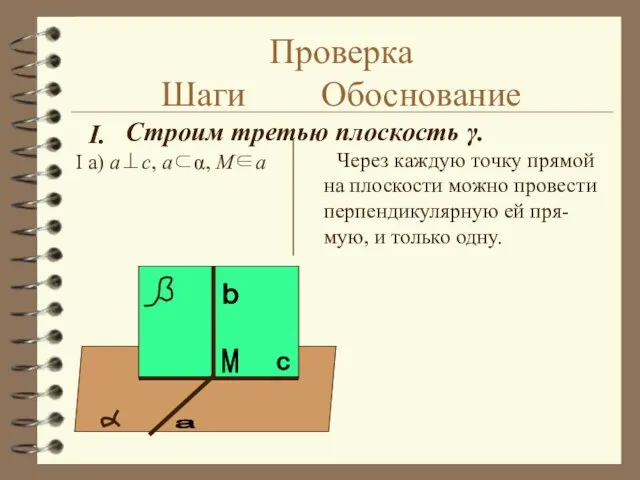
- 12. Проверка Шаги Обоснование I а) a⊥c, a⊂α, Μ∈a Через каждую точку прямой на плоскости можно провести
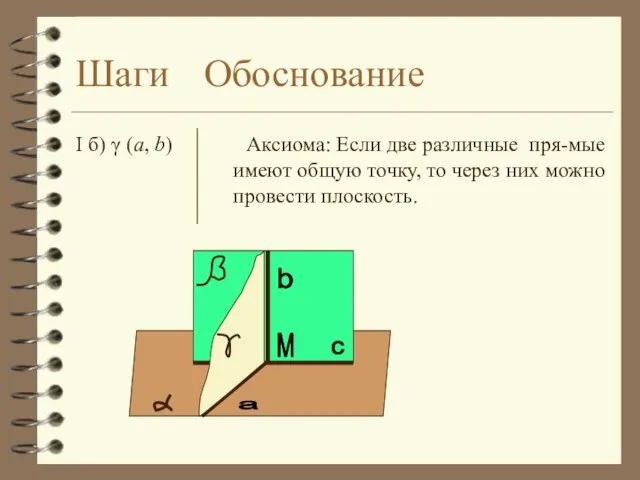
- 13. b c М а Шаги Обоснование I б) γ (а, b) Аксиома: Если две различные пря-мые
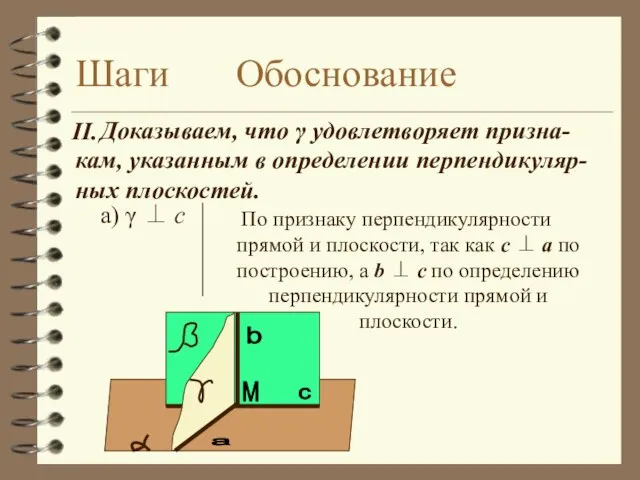
- 14. Шаги Обоснование а) γ ⊥ c По признаку перпендикулярности прямой и плоскости, так как с ⊥
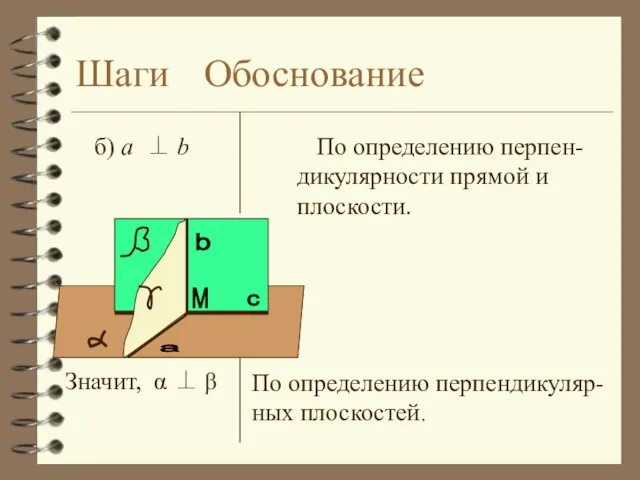
- 15. Шаги Обоснование б) a ⊥ b По определению перпен-дикулярности прямой и плоскости. Значит, α ⊥ β
- 16. Оформление доказательства: I. Строим плоскость γ: а) a ⊥ c, a ⊂ α, Μ ∈ a
- 18. Скачать презентацию








 Решите неравенства
Решите неравенства Числовые и буквенные выражения
Числовые и буквенные выражения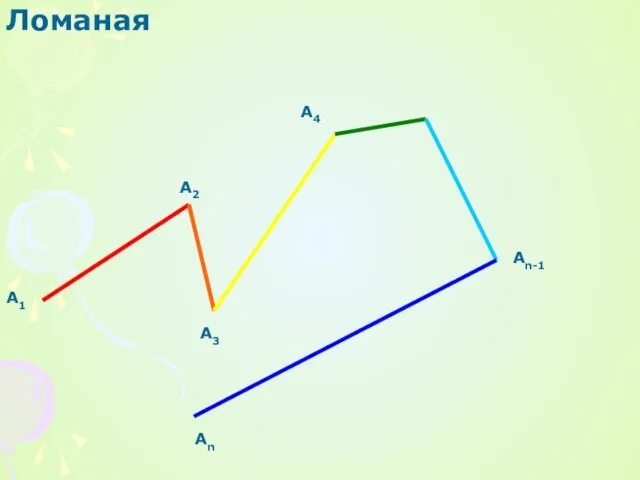 Презентация на тему Ломаная
Презентация на тему Ломаная  Первообразная. Интеграл. Площадь криволинейной трапеции
Первообразная. Интеграл. Площадь криволинейной трапеции Математическая статистика
Математическая статистика Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника
Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника Презентация на тему Целое и части (1 класс)
Презентация на тему Целое и части (1 класс)  Построение сечений
Построение сечений Aproximarea numerică a funcţiilor. Metode numerice – curs 11
Aproximarea numerică a funcţiilor. Metode numerice – curs 11 Презентация на тему КОМПЛЕКСНЫЕ ЧИСЛА
Презентация на тему КОМПЛЕКСНЫЕ ЧИСЛА  Серединный перпендикуляр
Серединный перпендикуляр Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа)
Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа) Сложение чисел
Сложение чисел Уравнение касательной к графику функции
Уравнение касательной к графику функции Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Площадь трапеции
Площадь трапеции Решение задач на вычисление площадей четырехугольников
Решение задач на вычисление площадей четырехугольников Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  Величины. Свойства величин
Величины. Свойства величин Функции. ЕГЭ
Функции. ЕГЭ Многочлены. Задания
Многочлены. Задания Формулы корней квадратных уравнений
Формулы корней квадратных уравнений Понятие площади. Площадь квадрата и прямоугольника
Понятие площади. Площадь квадрата и прямоугольника Умножение. Законы умножения
Умножение. Законы умножения Презентация на тему Показательная и логарифмическая функции
Презентация на тему Показательная и логарифмическая функции  Комбинаторика. Из истории комбинаторики
Комбинаторика. Из истории комбинаторики Влияние коэффициентов квадратного трехчлена на расположение параболы
Влияние коэффициентов квадратного трехчлена на расположение параболы Пушкин и математика
Пушкин и математика