Содержание
- 2. Сложение (вычитание) комплексных чисел Примеры: 1. 2.
- 3. Произведение и частное комплексных чисел в алгебраической форме. Произведение: Частное:
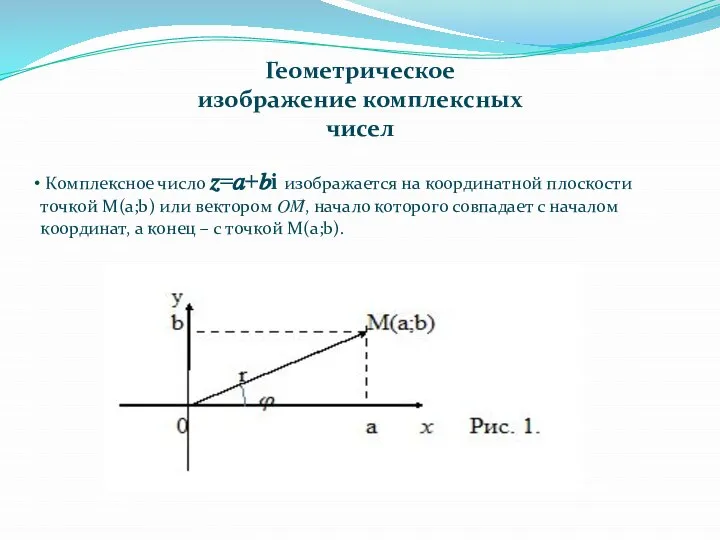
- 4. Геометрическое изображение комплексных чисел Комплексное число ?=?+?i изображается на координатной плоскости точкой М(a;b) или вектором ??⃗,
- 5. Модуль и аргумент комплексного числа Определение . Модулем комплексного числа называется абсолютная величина вектора, соответствующего этому
- 6. Определение. Аргументом комплексного числа ?≠0 называется величина угла между положительным направлением оси Оx и вектором, соответствующим
- 7. Правило нахождения аргумента комплексного числа 1. Найти tg ? =|?/?|. 2. Найти ?=arctg|?/?|. 3. Выяснив, в
- 8. Примеры: Найти модуль и аргумент комплексного числа.
- 11. Тригонометрическая форма комплексного числа Пусть дано комплексное число ?=?+?i Из ∆ ОМА можно выразить действительные числа
- 12. Правило перехода от алгебраической формы записи комплексного числа к тригонометрической Для того чтобы перейти от алгебраической
- 13. Примечание Модули и аргументы действительных чисел и чисто мнимых чисел надо находить непосредственно исходя из их
- 14. Пример: Комплексное число изобразить на плоскости и записать в тригонометрической форме 2 2 φ x y
- 15. Действия над комплексными числами в тригонометрической форме 1. Умножение
- 16. 2. Деление
- 17. Произведение и частное комплексных чисел в тригонометрической форме. Произведение: Частное:
- 18. 4. Извлечение корня из комплексного числа. 3. Возведение в степень
- 20. Комплексное в показательной (или экспонентной) форме Где и В силу формулы Эйлера функция периодическая с основным
- 21. Произведение и частное комплексных чисел в показательной форме.
- 22. Возведение комплексных чисел в степень. Правило умножения комплексных чисел позволяет возвести число в n-степень: Получим Формулу
- 23. Возведение комплексных чисел в степень. Пример. Найти Запишем число в тригонометрической форме:
- 24. Домашнее задание 1. Изобразить на координатной плоскости числа: 1. ? = 5; 4. z = 5
- 25. 3. Выполнить действия над комплексными числами в тригонометрической и показательной форме
- 27. Скачать презентацию























 Функция y=k/x, её график и свойства. 8 класс. Урок 2
Функция y=k/x, её график и свойства. 8 класс. Урок 2 Квадратный трехчлен. Самостоятельная работа
Квадратный трехчлен. Самостоятельная работа Решение задач разными арифметическими способами
Решение задач разными арифметическими способами Проценты
Проценты HMM выравнивание
HMM выравнивание Повторюємо арифметичні дії множення і ділення
Повторюємо арифметичні дії множення і ділення Презентация на тему Теорема о трех перпендикулярах
Презентация на тему Теорема о трех перпендикулярах  Решение задач. Геометрия, 8 класс
Решение задач. Геометрия, 8 класс Математика 1 класс
Математика 1 класс Решение прикладных задач с помощью свойств квадратичной функции
Решение прикладных задач с помощью свойств квадратичной функции Решение задач по теме Многогранники
Решение задач по теме Многогранники Критическое мышление
Критическое мышление Интерактивные Крестики-нолики. Задачи на готовых чертежах. Сумма углов треугольника
Интерактивные Крестики-нолики. Задачи на готовых чертежах. Сумма углов треугольника Понятие дифференциала. Приложение дифференциала
Понятие дифференциала. Приложение дифференциала Задача о баскетболисте. Расчетная работа №1
Задача о баскетболисте. Расчетная работа №1 Прибавление и вычитание числа 3. Помоги белочке
Прибавление и вычитание числа 3. Помоги белочке Квадратные уравнения
Квадратные уравнения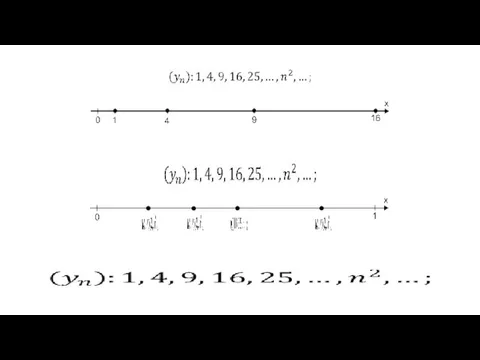 Пояснения к определению предела последовательности
Пояснения к определению предела последовательности Признаки равенства треугольников
Признаки равенства треугольников Фрактальное изображение
Фрактальное изображение Подготовка к контрольной работе
Подготовка к контрольной работе История возникновения геометрии как науки
История возникновения геометрии как науки Геометрические преобразования в пространстве
Геометрические преобразования в пространстве Презентация на тему Длина окружности и площадь круга (9 класс)
Презентация на тему Длина окружности и площадь круга (9 класс)  СМО
СМО Collatz Conjecture
Collatz Conjecture Найти корень уравнения. Тест. Задания В5, ЕГЭ по математике
Найти корень уравнения. Тест. Задания В5, ЕГЭ по математике Упражнения по планиметрии на готовых чертежах. VII класс
Упражнения по планиметрии на готовых чертежах. VII класс