Содержание
- 2. Решить уравнения: cos t = ; cos t = 1.
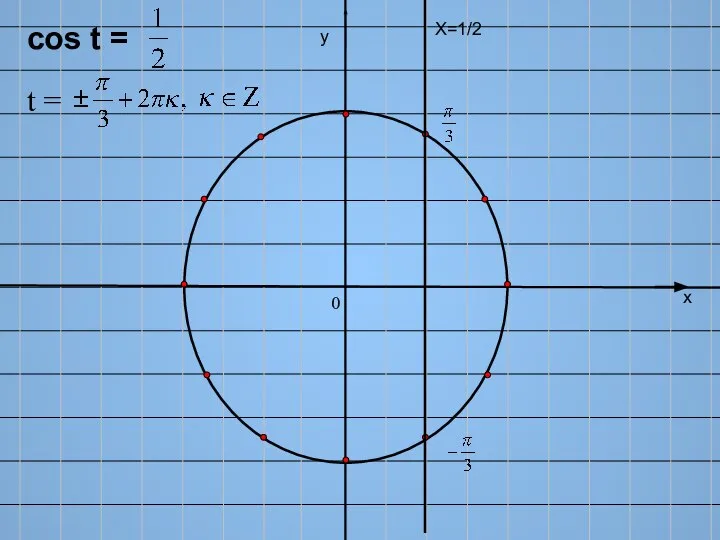
- 3. х у Х=1/2 cos t = t = 0
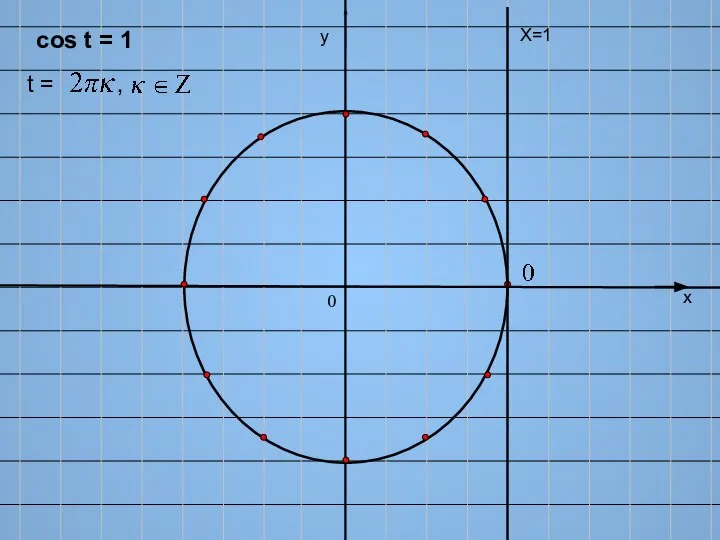
- 4. х у Х=1 cos t = 1 t = , 0
- 5. Решить уравнение: cos t = .
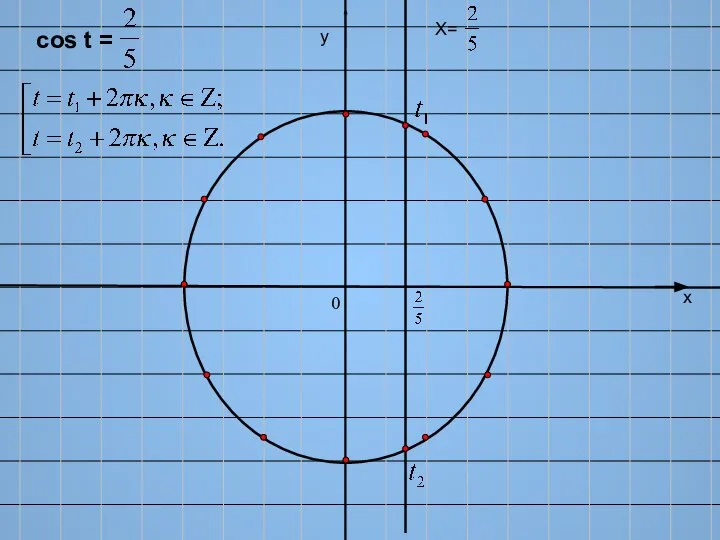
- 6. х у Х= cos t = 0
- 7. arccos а Читается: арккосинус а «arcus» в переводе с латинского значит «дуга» (сравните со словом «арка»)
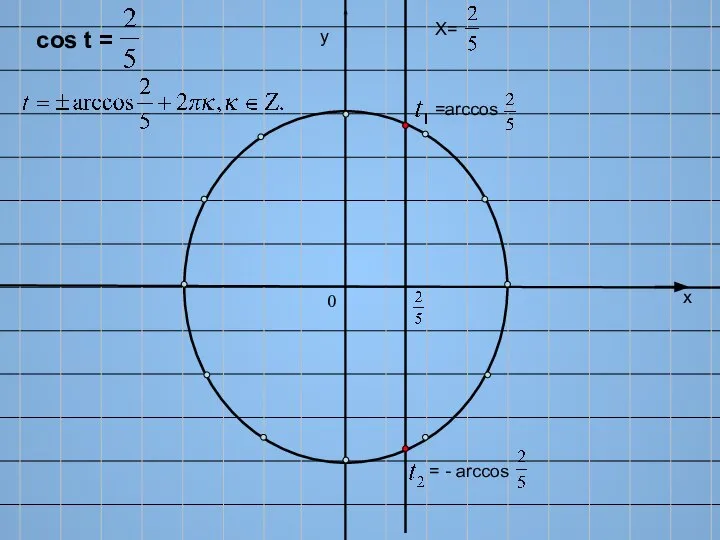
- 8. х у Х= cos t = =arccos = - arccos 0
- 9. Что же такое ? arccos Это число (длина дуги), косинус которого равен и которое принадлежит первой
- 10. Решить уравнение: cos t = .
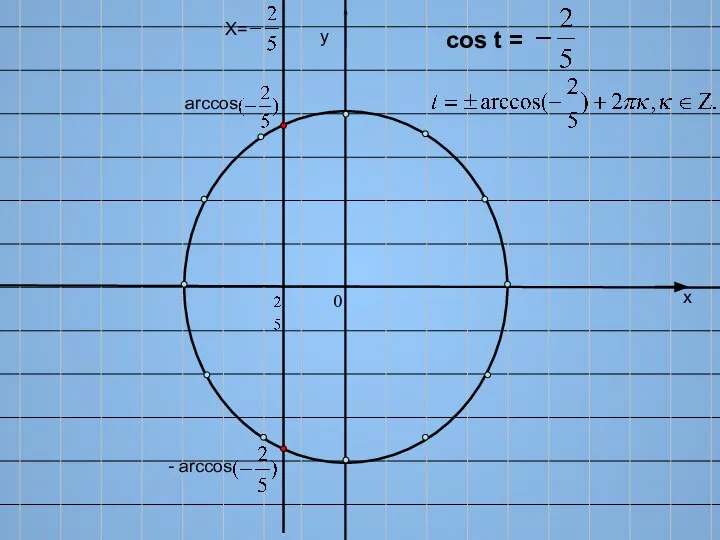
- 11. х у Х= cos t = arccos - arccos 0
- 12. Что же такое ? arccos Это число (длина дуги), косинус которого равен и которое принадлежит второй
- 13. Определение. Если │a│
- 14. Пример 1 arccos = t =?
- 15. Пример 2 arccos = t =?
- 16. Пример 3 arccos = t =?
- 17. Пример 4 arccos = t =?
- 18. Решение уравнения cos t = a. Если │a│ , то уравнение cost = a имеет решения:
- 19. Частные случаи: 1) Если cos t = 0, то t = , 2) Если cos t
- 20. Для любого а [-1;1] выполняется равенство arccos a + arccos (-a) = Теорема. а -а 0
- 21. arccos (-a) = - arccos a , где На практике используется: Пример. arccos = - arccos
- 22. Решение уравнений Пример 1. cos t = , = arccos
- 23. Вычислим
- 24. Решение уравнений Пример 1. cos t = , = arccos a , Ответ:
- 25. Решение уравнений Пример 2. cos t = , = arccos a
- 26. arccos = - arccos = Вычислим
- 27. Решение уравнений Пример 2. cos t = , = arccos a , Ответ:
- 28. Решение уравнений Пример 3. cos t = , = arccos a Ответ: }, { arccos a
- 29. Решение уравнений Пример 4. cos t = Ответ: уравнение решения не имеет. - 1
- 31. Скачать презентацию

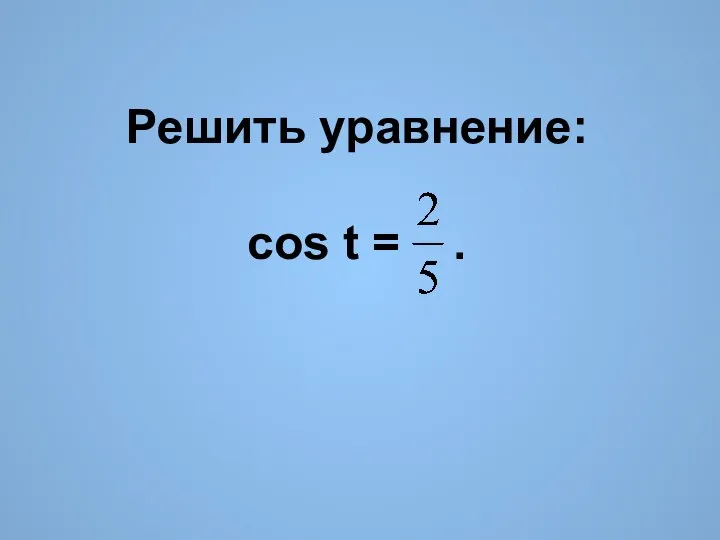


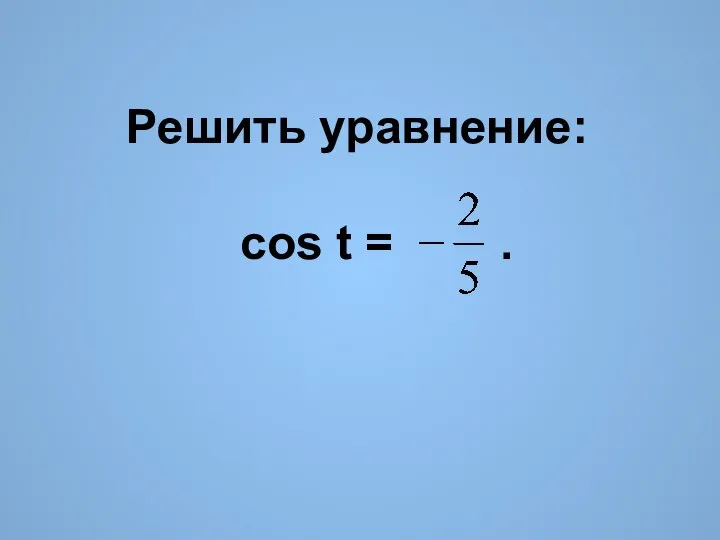








![Для любого а [-1;1] выполняется равенство arccos a + arccos (-a) = Теорема. а -а 0](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/940669/slide-19.jpg)


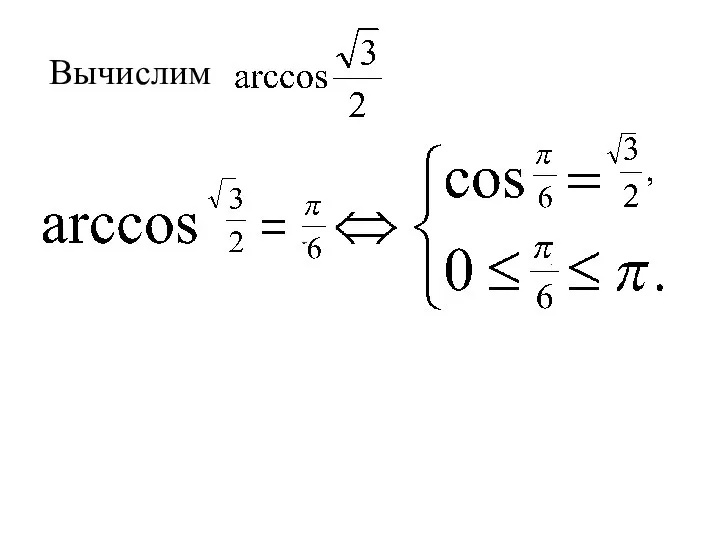


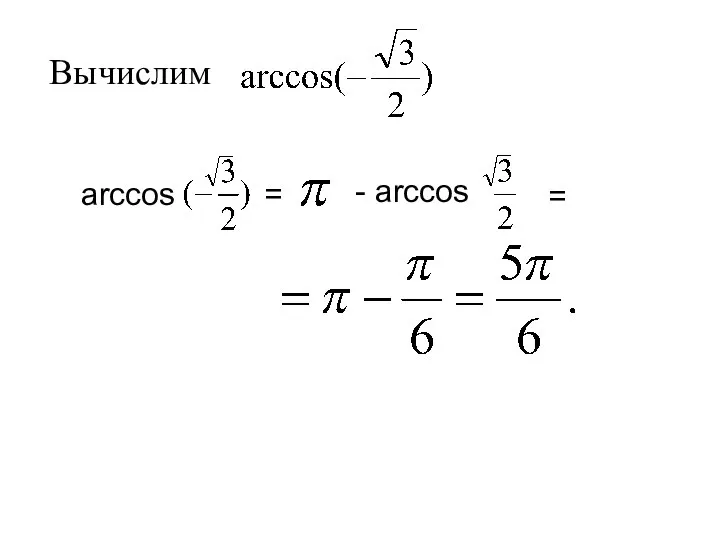



 Отношения и золотое сечение
Отношения и золотое сечение Умножение дробей. Анаграммы
Умножение дробей. Анаграммы Нахождение дроби от числа
Нахождение дроби от числа Презентация на тему Объем цилиндра
Презентация на тему Объем цилиндра  История развития обыкновенных дробей
История развития обыкновенных дробей polupravilnye-mnogogranniki
polupravilnye-mnogogranniki Введение в дисциплину Математические модели в экологических системах
Введение в дисциплину Математические модели в экологических системах Площадь. Площадь прямоугольника. 5 класс
Площадь. Площадь прямоугольника. 5 класс Проценты и десятичные дроби
Проценты и десятичные дроби Выражения, содержащие степень с целым показателем
Выражения, содержащие степень с целым показателем Тетраэдр
Тетраэдр logarif_uravnenia
logarif_uravnenia Окружность и круг
Окружность и круг Пустое множество
Пустое множество Задания по математике (5 класс, часть 1)
Задания по математике (5 класс, часть 1) Pervoobraznaya
Pervoobraznaya Что такое дискретная математика?
Что такое дискретная математика? Делимость чисел
Делимость чисел Математика вокруг нас
Математика вокруг нас Случайный выбор точки из отрезка
Случайный выбор точки из отрезка Презентация на тему Устный счёт 1 класс
Презентация на тему Устный счёт 1 класс  Исследуйте выражения
Исследуйте выражения Сумма углов треугольника. 7 класс
Сумма углов треугольника. 7 класс Метрология, основные понятия
Метрология, основные понятия Повторение и расширение сведений о функции
Повторение и расширение сведений о функции Описательная статистика
Описательная статистика Задача на тему: Прогрессия
Задача на тему: Прогрессия Тригонометрия (В5, В7) на ЕГЭ
Тригонометрия (В5, В7) на ЕГЭ