Содержание
- 2. Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К таким уравнениям относятся
- 3. Простейшие тригонометрические уравнения
- 4. Общий случай: Частный случай:
- 5. Общий случай: Частный случай:
- 7. Арксинус ,арккосинус, арктангенс, арккотангенс Арксинусом числа а называется такое число из отрезка , синус которого равен
- 8. Методы решения тригонометрических уравнений
- 9. 1.Метод введения переменной Уравнения, представляющие собой квадратные уравнения относительно какой-либо тригоно-метрической функции. Если в уравнение входят
- 10. 2. МЕТОД РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ Произведение нескольких множителей равно нулю, если хотя бы один из множителей
- 11. 1. Если а=0, то уравнение примет вид: если b=0, то уравнение примет вид: . 2. Рассмотрим
- 12. , 1. если , то , Уравнение вида называется однородным тригонометрическим уравнением второй степени. 2. если
- 14. Скачать презентацию




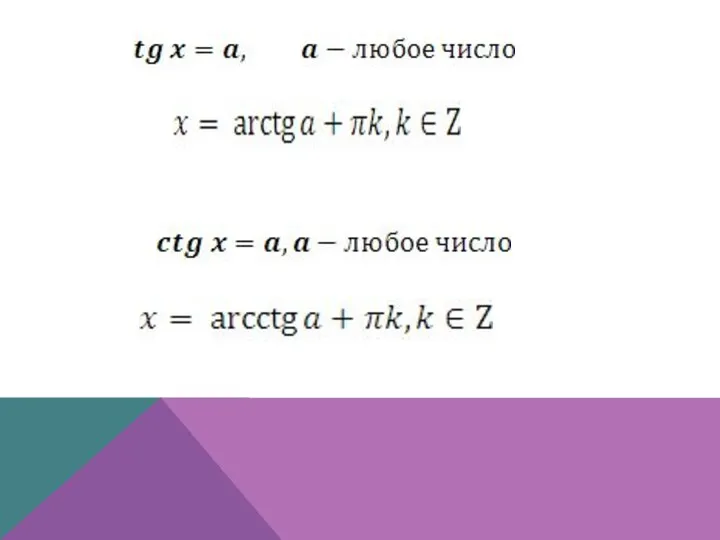






 Алгоритмы на графах
Алгоритмы на графах Устная нумерация чисел от 1 до 20
Устная нумерация чисел от 1 до 20 Числовi послiдовностi. Властивостi числових послiдовностей
Числовi послiдовностi. Властивостi числових послiдовностей Решение тригонометрических уравнений
Решение тригонометрических уравнений Окружность
Окружность Предел последовательности
Предел последовательности Знак деления
Знак деления Деление одночлена на одночлен
Деление одночлена на одночлен Решаем задачи
Решаем задачи Системы принятия решений
Системы принятия решений Возвратные уравнения
Возвратные уравнения Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики?
Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики? Куб. Теорема Эйлера
Куб. Теорема Эйлера Решение иррациональных уравнений. Разные методы
Решение иррациональных уравнений. Разные методы Решение тригонометрических неравенств
Решение тригонометрических неравенств Тригонометрические уравнения и математические термины на английском языке
Тригонометрические уравнения и математические термины на английском языке Сложение и вычитание многочленов
Сложение и вычитание многочленов Производная функции. Тест 1
Производная функции. Тест 1 Основы дисперсионного анализа
Основы дисперсионного анализа Неопределённый интеграл. Элементы интегрального исчисления
Неопределённый интеграл. Элементы интегрального исчисления Сравнение предметов. Счет до 5
Сравнение предметов. Счет до 5 Формулы половинного аргумента
Формулы половинного аргумента Пирамида и её элементы. Правильная пирамида
Пирамида и её элементы. Правильная пирамида Шар. Куб. Параллелепипед
Шар. Куб. Параллелепипед Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна
Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна Таблицы истинности
Таблицы истинности Плоскость касательной к сфере
Плоскость касательной к сфере Задачи на готовых чертежах. Ромб
Задачи на готовых чертежах. Ромб