Содержание
- 2. Повторим Касательная к окружности – это прямая, имеющая с окружностью одну общую точку. Через любую точку
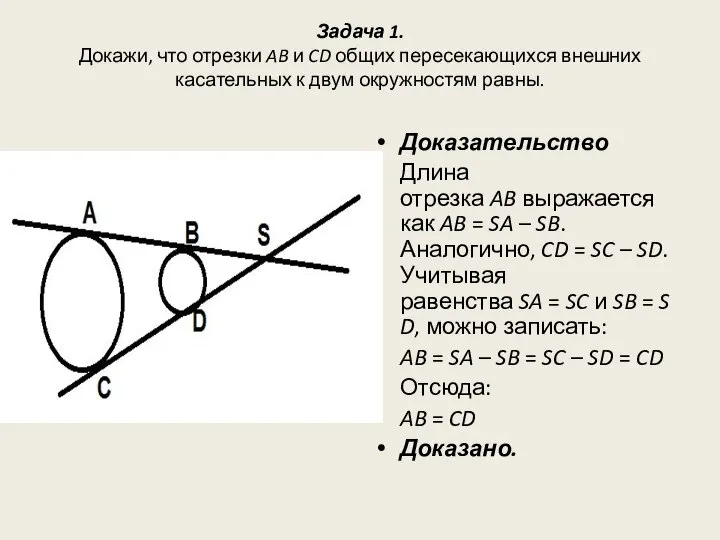
- 3. Задача 1. Докажи, что отрезки AB и CD общих пересекающихся внешних касательных к двум окружностям равны.
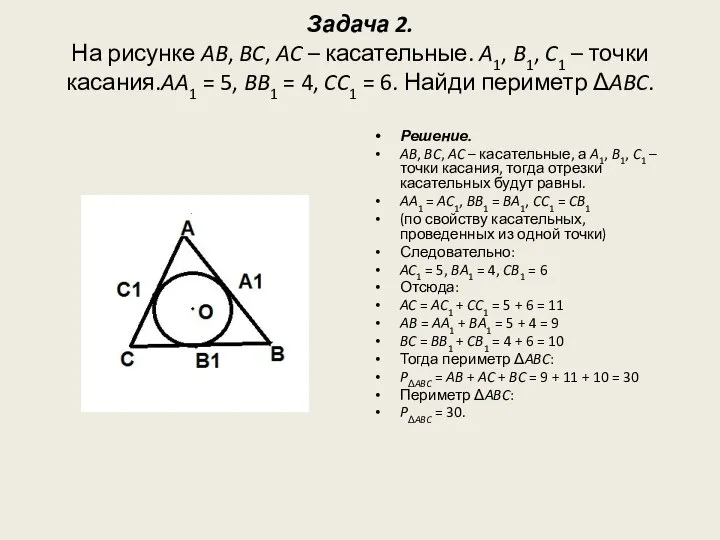
- 4. Задача 2. На рисунке AB, BC, AC – касательные. A1, B1, C1 – точки касания.AA1 =
- 5. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
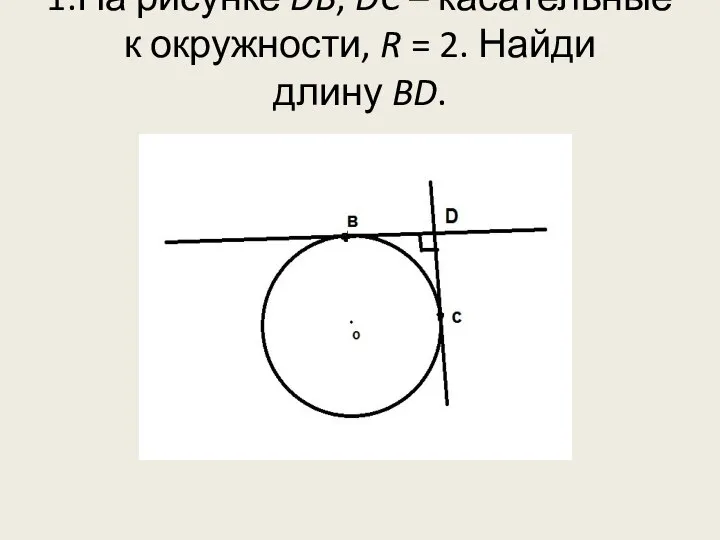
- 6. 1.На рисунке DB, DC – касательные к окружности, R = 2. Найди длину BD.
- 7. Решение Так как DB, DC – касательные, то они перпендикулярны радиусу окружности. Эти отрезки проведены из
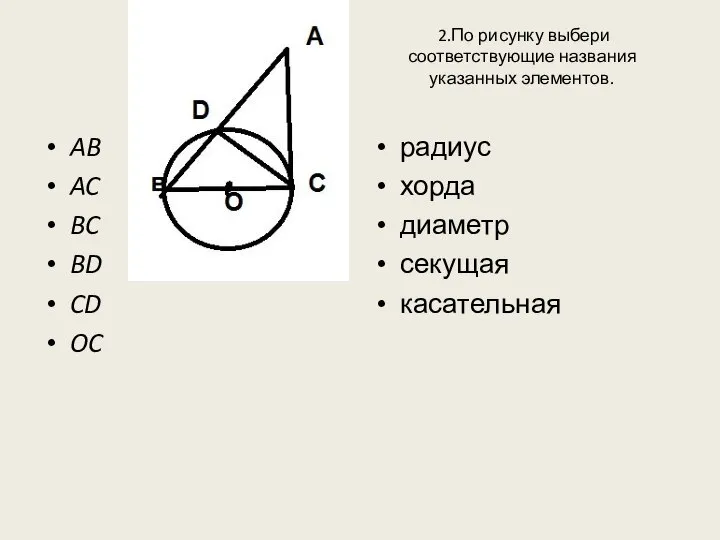
- 8. 2.По рисунку выбери соответствующие названия указанных элементов. AB AC BC BD CD OC радиус хорда диаметр
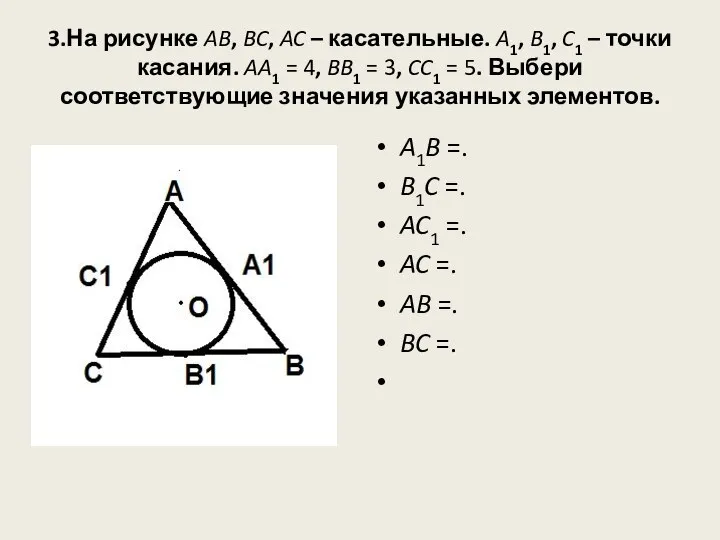
- 9. 3.На рисунке AB, BC, AC – касательные. A1, B1, C1 – точки касания. AA1 = 4,
- 10. Решение A1B =3 B1C =5 AC1 =4 AC = 9 AB =7 BC =8 AB, BC,
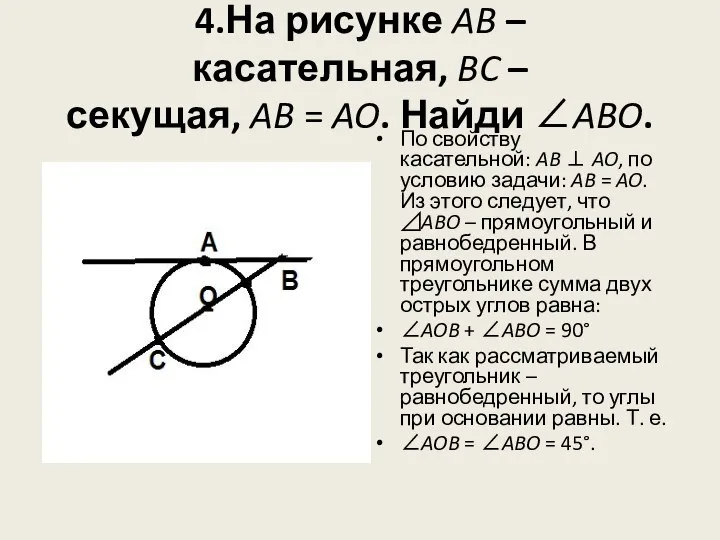
- 11. 4.На рисунке AB – касательная, BC – секущая, AB = AO. Найди ∠ABO. По свойству касательной:
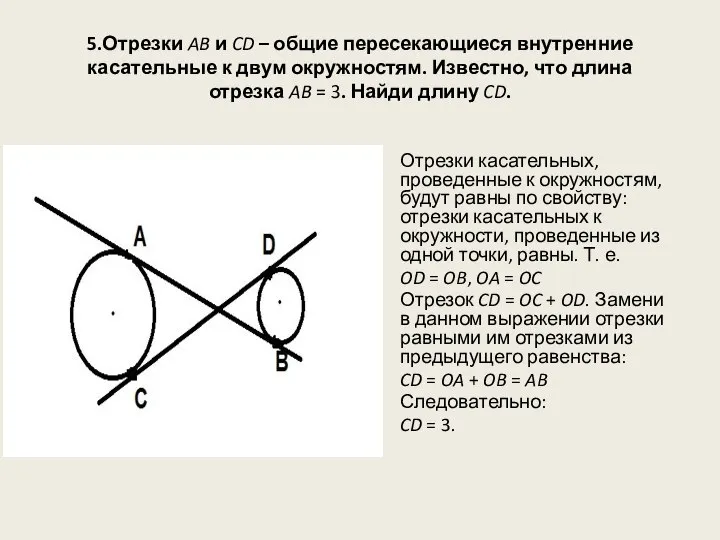
- 12. 5.Отрезки AB и CD – общие пересекающиеся внутренние касательные к двум окружностям. Известно, что длина отрезка
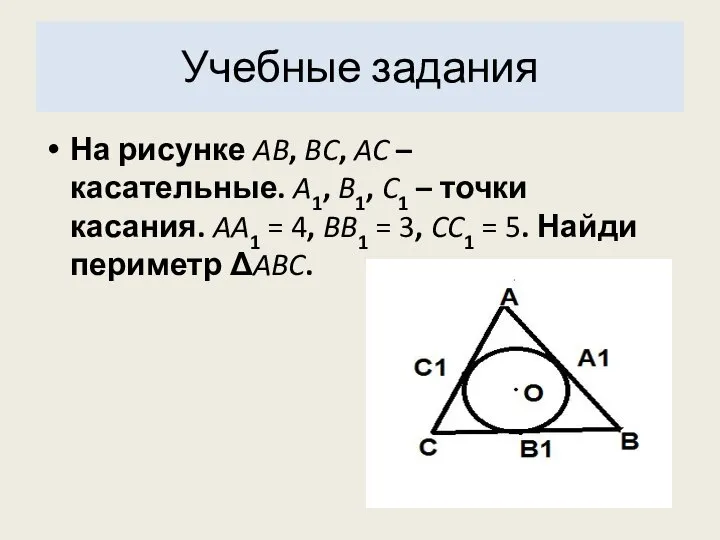
- 13. Учебные задания На рисунке AB, BC, AC – касательные. A1, B1, C1 – точки касания. AA1
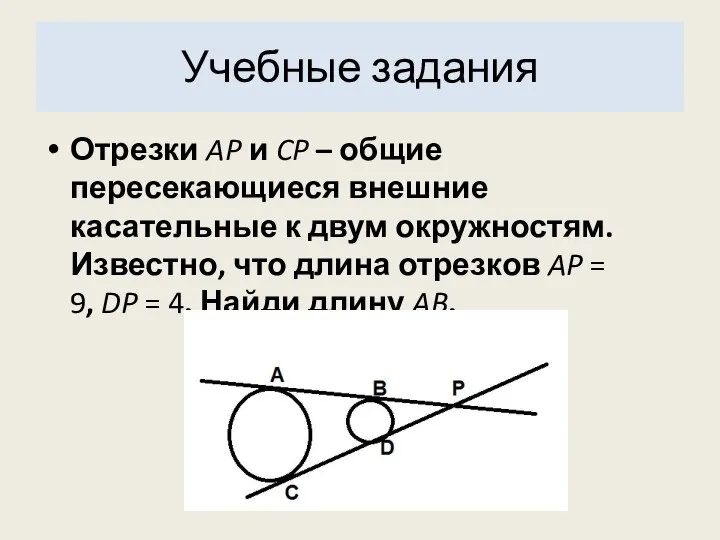
- 14. Учебные задания Отрезки AP и CP – общие пересекающиеся внешние касательные к двум окружностям. Известно, что
- 16. Скачать презентацию




 Без знаний дробей никто не может признаваться знающим арифметику
Без знаний дробей никто не может признаваться знающим арифметику Определитель и его свойства
Определитель и его свойства Өзіңді – өзің тексер! Мақсаты: оқушылардың білім деңгейын анықтау
Өзіңді – өзің тексер! Мақсаты: оқушылардың білім деңгейын анықтау Математика на каждый день
Математика на каждый день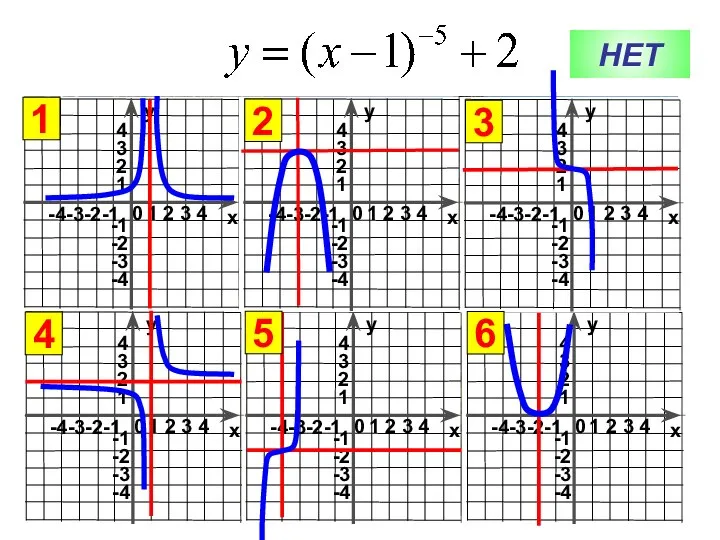 графики функций. Ошибка
графики функций. Ошибка Общий прием сложения
Общий прием сложения Вектор Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом.
Вектор Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом. Результант. Литература
Результант. Литература Степень числа
Степень числа деление обыкновенных дробей
деление обыкновенных дробей Прямо-пропорциональные величины
Прямо-пропорциональные величины Генеалогическое древо семьи Бернулли
Генеалогическое древо семьи Бернулли Решение задач
Решение задач Урок математики во 2 классе. Повторение
Урок математики во 2 классе. Повторение Пропорции в нашем мире
Пропорции в нашем мире Формулы сложных процентов в задачах с финансово-экономическим содержанием
Формулы сложных процентов в задачах с финансово-экономическим содержанием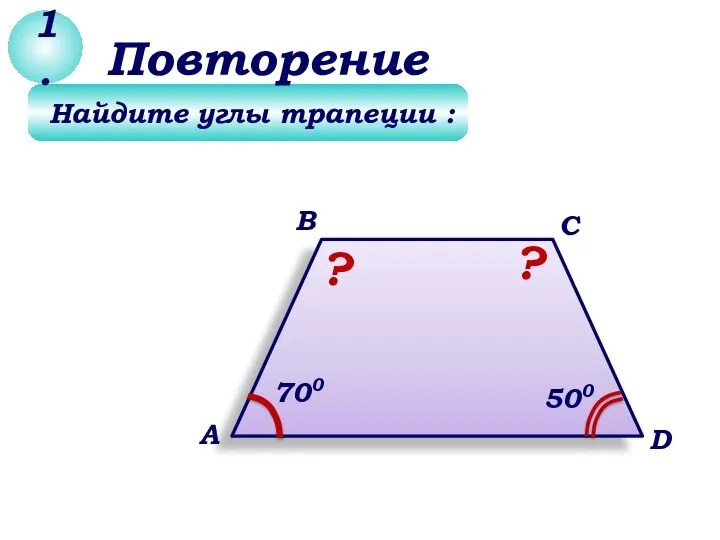 Задачи по геометрия 8 класс
Задачи по геометрия 8 класс Статистический анализ экспериментальных данных
Статистический анализ экспериментальных данных Векторы
Векторы Графический диктант: Формулы
Графический диктант: Формулы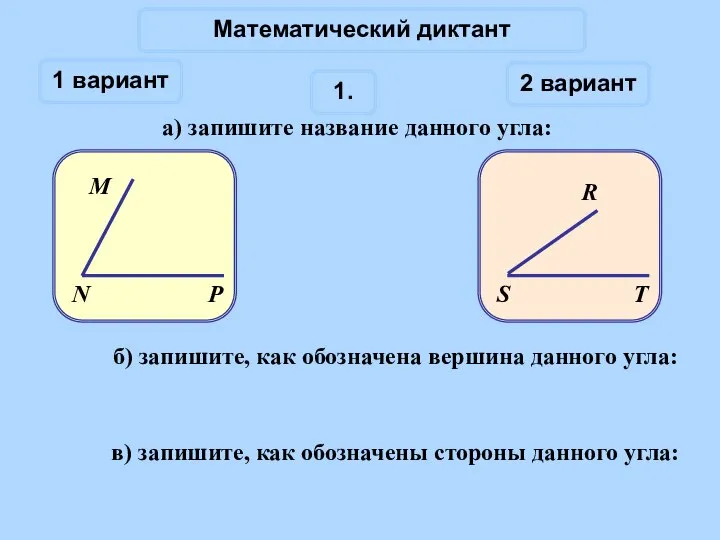 Углы. Математический диктант
Углы. Математический диктант Задачи на пропорциональное деление
Задачи на пропорциональное деление Проценты
Проценты Определение неизвестного числа
Определение неизвестного числа Класс точности средств измерений
Класс точности средств измерений Мифы о Николае Ивановиче Лобачевском и его геометрии
Мифы о Николае Ивановиче Лобачевском и его геометрии Мой любимый предмет – геометрия. Геометрия – прообраз красоты мира. И. Кеплер. 11 класс
Мой любимый предмет – геометрия. Геометрия – прообраз красоты мира. И. Кеплер. 11 класс Об учебниках по геометрии и теоремах в них. Признаки параллельных и скрещивающихся прямых, параллельности прямой и плоскости
Об учебниках по геометрии и теоремах в них. Признаки параллельных и скрещивающихся прямых, параллельности прямой и плоскости