Содержание
- 2. Пусть - отношение на , а - отношение на Композицией отношений S и R называется отношение
- 3. Это множество обозначается
- 4. Пример: Даны, множества A = {1,2,3}, B = {x,y}, С = {♦, ♥, ♣, ♠}. Отношения
- 6. Тогда
- 7. Теорема. Композиция отношений ассоциативна; т.е. если А, В, и С – множества и если , тогда
- 8. Виды отношений
- 9. В зависимости от того, какими свойствами обладает отношения, они делятся на три вида; отношение эквивалентности, отношение
- 10. Бинарное отношение R на множестве A2 называется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности и
- 11. Эквивалентные элементы (т.е. находящиеся в отношении эквивалентности), как правило, обладают какими-то общими признаками.
- 12. Пример А = {1,2,3,4,5,6}, R = {(1,1), (2,2), (3,3), (4,4),(5,5), (6,6), (1,2), (1,4), (2,1), (2,4), (3,5),
- 13. Если на множестве задано отношение эквивалентности, то все его элементы можно разбить на непересекающиеся подмножества, состоящие
- 14. Разбиением множества А называется совокупность попарно непересекающихся непустых подмножеств А1, А2, …, Аn из множества А
- 15. Пусть а А, и R отношение эквивалентнос ти на А А. Пусть [а] обозначает множество называемое
- 16. Пример А = {1,2,3,4,5,6}, R = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (1,2), (1,4), (2,1), (2,4),
- 17. Класс эквивалентности по отношению к R получаются путем определения класса эквивалентности каждого элемента множества А.
- 24. Имеется только три различных класса эквивалентности
- 25. Выводы Любой элемент класса эквивалентности порождает класс эквивалентности: если . На основании этого свойства следует, что
- 26. Каждый класс эквивалентности содержит по крайней мере, один элемент, в силу рефлексивности отношении. Множество всех элементов,
- 27. Отношение эквивалентности разбивает множество А на попарно непересекающиеся классы эквивалентных элементов, таким образом, что каждый элемент
- 28. 1. Всякое разбиение множества А на классы задает на множестве А отношение эквивалентности. 2. Всякое отношение
- 29. Отношение порядка
- 30. Отношение R на множестве A2 называется отношением частичного порядка, если оно обладает свойствами рефлексивности, антисимметричности, транзитивности.
- 31. Множество А вместе с заданным на нем отношением частичного порядка R называется частично упорядоченным множеством (ЧУ-множеством
- 32. Если для двух элементов x и y выполняется x ≤ y, то говорят, что x «предшествует»
- 33. Однако, если х предшествует у, и не существует таких элементов z, для которых хRz и zRy,
- 34. Элементы а и b частично упорядоченного множества (А, ≤) называется сравнимыми, если а ≤ b или
- 35. Другими словами линейным порядком на множестве А называется отношение частичного порядка, при котором из любой пары
- 36. Пример линейного порядка: «≤» на множестве вещественных чисел, лексикографическое упорядочение слов в словаре.
- 37. Если каждые два элемента частично упорядоченные множества (А, ≤) сравнимы, то (А, ≤) называется вполне упорядоченным
- 38. Простым примером отношения порядка является отношение, задаваемое обычным неравенством ≤ на множестве вещественных чисел R.
- 39. Рассмотрим на множестве A всех сотрудников некоторого предприятия. Отношение, задается следующим образом: сотрудник x предшествует сотруднику
- 40. Назовем такое отношение «быть начальником». Отношение «быть начальником» является отношением порядка.
- 41. Поскольку существуют такие пары сотрудников x и y, для которых не выполняется ни x ≤ y,
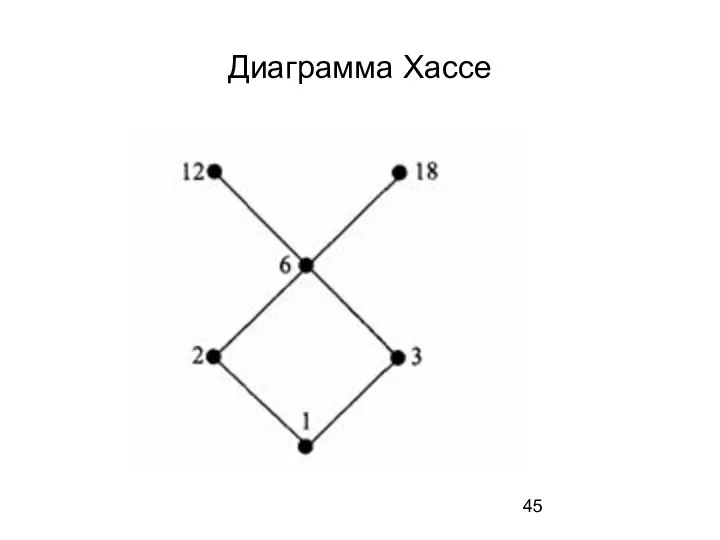
- 42. Вершины графа изображают элементы ЧУ-множества А, и если x y., то вершина х помещается ниже вершины
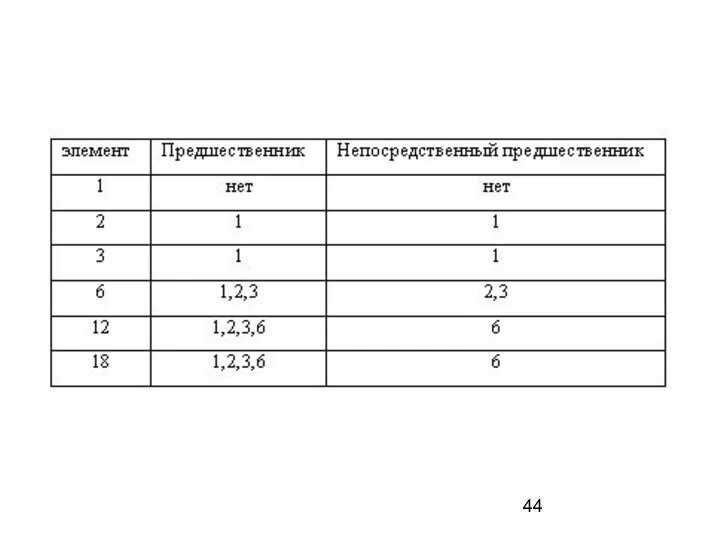
- 43. Пример: Дано отношение «…делитель…» определяет частичный порядок на множестве А = {1,2,3,6,12,18}. Составить таблицу предшественников и
- 45. Диаграмма Хассе
- 48. Скачать презентацию

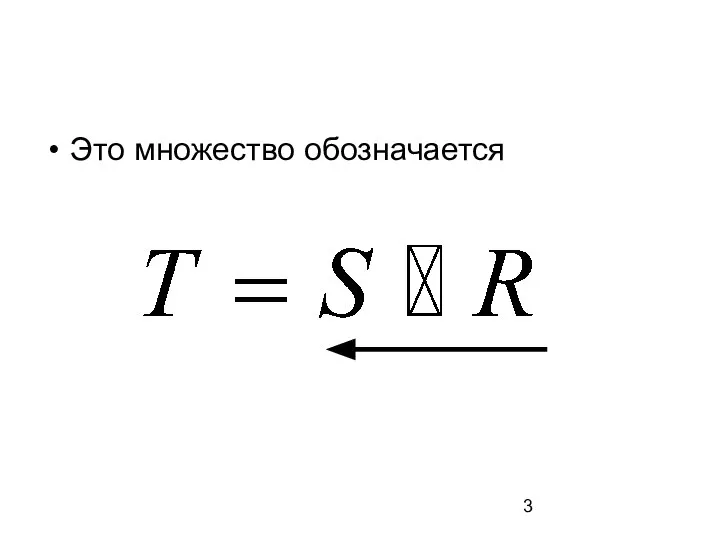

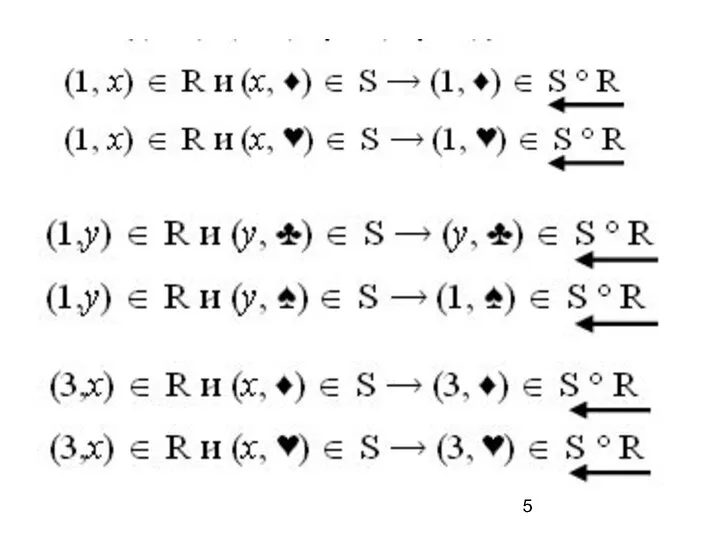







































 Доверительные интервалы
Доверительные интервалы Длиннее, короче, одинаковые по длине. Математическая сказка
Длиннее, короче, одинаковые по длине. Математическая сказка Обратные тригонометрические функции, их графики и формулы
Обратные тригонометрические функции, их графики и формулы Планиметрия: вычисление площади треугольника
Планиметрия: вычисление площади треугольника Задачи с экономическим содержанием
Задачи с экономическим содержанием Элементы математической статистики. Теория вероятностей
Элементы математической статистики. Теория вероятностей Таблица умножения и деления. Тренажёр на скорость
Таблица умножения и деления. Тренажёр на скорость Шар и сфера
Шар и сфера Письменный прием вычитания
Письменный прием вычитания Презентация на тему Умножение числа 2
Презентация на тему Умножение числа 2  Функция, ее график и свойства
Функция, ее график и свойства Таблица. Алгебра
Таблица. Алгебра Основные понятия дискретной математики
Основные понятия дискретной математики Вариационный ряд. Группировка данных при качественной и количественной вариациях
Вариационный ряд. Группировка данных при качественной и количественной вариациях Решите систему неравенств и укажите все целые числа, которые являются ее решениями
Решите систему неравенств и укажите все целые числа, которые являются ее решениями Задачи на построение
Задачи на построение Магический квадрат. 2 класс
Магический квадрат. 2 класс Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4
Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4 Природа России в цифрах и загадках
Природа России в цифрах и загадках Действия над матрицами. Вычисление определителей второго и третьего порядков
Действия над матрицами. Вычисление определителей второго и третьего порядков Соответствия между множествами. Отображения. Функции
Соответствия между множествами. Отображения. Функции Математическая модель колонны многокомпонентной ректификации. Лекция 9
Математическая модель колонны многокомпонентной ректификации. Лекция 9 Научные открытия России. Задача тысячелетия. Теорема Пуанкаре
Научные открытия России. Задача тысячелетия. Теорема Пуанкаре Презентация на тему Свойства логарифмов (10 класс)
Презентация на тему Свойства логарифмов (10 класс)  Графики уравнений
Графики уравнений Презентация на тему СТЕПЕНЬ С ЦЕЛЫМ ОТРИЦАТЕЛЬНЫМ ПОКАЗАТЕЛЕМ
Презентация на тему СТЕПЕНЬ С ЦЕЛЫМ ОТРИЦАТЕЛЬНЫМ ПОКАЗАТЕЛЕМ  Личные местоимения
Личные местоимения Таблица умножение на двух значное число
Таблица умножение на двух значное число