Слайд 2Формула полной вероятности
Если событие А может произойти только при выполнении одного из

событий
,
которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
Эта формула называется формулой полной вероятности.
Слайд 3Формула Байеса (Бейеса)
Вновь рассмотрим полную группу несовместных событий
, вероятности появления которых
Событие А

может произойти только вместе с каким-либо из событий , которые будем называть гипотезами.
Тогда по формуле полной вероятности
Как определить вероятность того, что имела место та или иная гипотеза?
Слайд 4Формула Байеса (Бейеса)
При условии, что событие уже произошло, вероятности гипотез переоцениваются по

формулам, которые получили фамилию английского священника Томаса Байеса:
– вероятность того, что имела место гипотеза В1
– вероятность того, что имела место гипотеза В2
– вероятность того, что имела место гипотеза В3
. . .
– вероятность того, что имела место гипотеза Вn
Слайд 5Формула Байеса (Бейеса)
На первый взгляд кажется полной нелепицей – зачем пересчитывать вероятности

гипотез, если они и так известны? Но на самом деле разница есть:
- это априорные (оцененные до испытания) вероятности.
- это апостериорные
(оцененные после испытания) вероятности тех же гипотез, пересчитанные в связи «со вновь открывшимися обстоятельствами» – с учётом того факта, что событие А достоверно произошло.
Слайд 6Формула Байеса (Бейеса)
Рассмотрим пример.
На склад поступило 2 партии изделий: первая – 4000

штук, вторая – 6000 штук.
Средний процент нестандартных изделий в первой партии составляет 20%, а во второй – 10%.
Наудачу взятое со склада изделие оказалось стандартным.
Найти вероятность того, что оно:
а) из первой партии,
б) из второй партии.
Слайд 7Формула Байеса (Бейеса)
Решение.
Первая часть решения состоит в использовании формулы полной вероятности. Иными

словами, вычисления проводятся в предположении, что испытание ещё не произведено и событие «изделие оказалось стандартным» пока не наступило.
Рассмотрим две гипотезы:
В1– наудачу взятое изделие будет из 1-й партии;
В2– наудачу взятое изделие будет из 2-й партии.
Всего: 4000 + 6000 = 10000 изделий на складе.
Слайд 8Решение.
По классическому определению:
Рассмотрим зависимое событие: А – наудачу взятое со склада изделие

будет стандартным.
В первой партии 100% – 20% = 80% стандартных изделий,
поэтому: - вероятность того, что наудачу взятое на складе изделие будет стандартным при условии, что оно принадлежит 1-й партии. Аналогично, во второй партии 100% – 10% = 90% стандартных изделий и
- вероятность того, что наудачу взятое на
складе изделие будет стандартным при условии, что оно принадлежит 2-й партии.
Слайд 9Решение.
По формуле полной вероятности:
– вероятность того, что наудачу взятое на складе

изделие будет стандартным.
Часть вторая. Пусть наудачу взятое со склада изделие оказалось стандартным. Эта фраза прямо прописана в условии, и она констатирует тот факт, что событие произошло. По формулам Байеса вероятность того, что выбранное стандартное изделие принадлежит 1-й партии:
вероятность того, что выбранное стандартное изделие принадлежит 2-й партии:
Слайд 10Задание 1.
На склад поступило 3 партии изделий: первая – 2000 штук, вторая

– 3000 штук, третья – 5000 штук.
Средний процент нестандартных изделий в первой партии составляет 5%, во второй – 10%, а в третьей – 15%.
Наудачу взятое со склада изделие оказалось стандартным.
Найти вероятность того, что оно:
а) из первой партии,
б) из второй партии,
в) из третьей партии.
Слайд 11Неравенство Маркова
Неравенство Маркова дает вероятностную оценку того, что значение неотрицательной случайной величины

превзойдет некоторую константу через известное математическое ожидание.
Когда никаких других данных о распределении нет, неравенство дает некоторую информацию, хотя зачастую оценка груба или тривиальна.
Слайд 12Неравенство Маркова
Пусть X - случайная величина, принимающая неотрицательные значения, M(X) - ее

конечное математическое ожидание, то для любых a>0
выполняется условие
Альтернативная форма записи (когда нужно оценить вероятность того, что случайная величина меньше некоторой константы):
Слайд 13Неравенство Маркова
Пример.
Среднее количество вызовов, поступающих на коммутатор завода в течение часа, равно

300.
Оценить вероятность того, что в течение следующего часа число вызовов на коммутатор:
а) превысит 400;
б) будет не более 500.
Слайд 14Неравенство Маркова
Решение.
По условию М(Х)=300.
а) Воспользуемся формулой (неравенством Маркова)
Тогда , т.е. вероятность

того,
что число вызовов превысит 400, будет не более 0,75.
Слайд 15Неравенство Маркова
Решение.
б) воспользуемся неравенством Маркова в альтернативном виде:
Тогда , т.е. вероятность

того,
что число вызовов не более 500, будет не менее 0,4.
Слайд 16Задание 2.
Количество потребляемой за сутки электроэнергии предприятием является случайной величиной с математическим

ожиданием 8 мегаватт.
Оценить вероятность того, что в ближайшие сутки потребление электроэнергии окажется:
а) более 10 мегаватт,
б) не более 12 мегаватт.
Слайд 17Неравенство Чебышева
Когда известны не только математическое ожидание, но и дисперсия для случайной

величины, можно применять следствие неравенства Маркова — неравенство Чебышева, которое дает оценку вида:
Также его можно записать в другой форме:
Неравенство Чебышева показывает, что случайная величина принимает значения близкие к среднему (математическому ожиданию) и дает оценку вероятности больших отклонений.
Слайд 18Неравенство Чебышева
Пример.
Генератор обеспечивает выходное напряжение, которое может отклоняться от номинального назначение, не

превышающее 1 В, с вероятностью 0,95. Какие значения дисперсии выходного напряжения можно ожидать?
Решение.
Пусть X - величина выходного напряжения. Применим неравенство Чебышева
Слайд 19Неравенство Чебышева
Подставляя наши данные ε=1, Р=0,95P, имеем:
Ответ: дисперсия не менее 0,05 .



















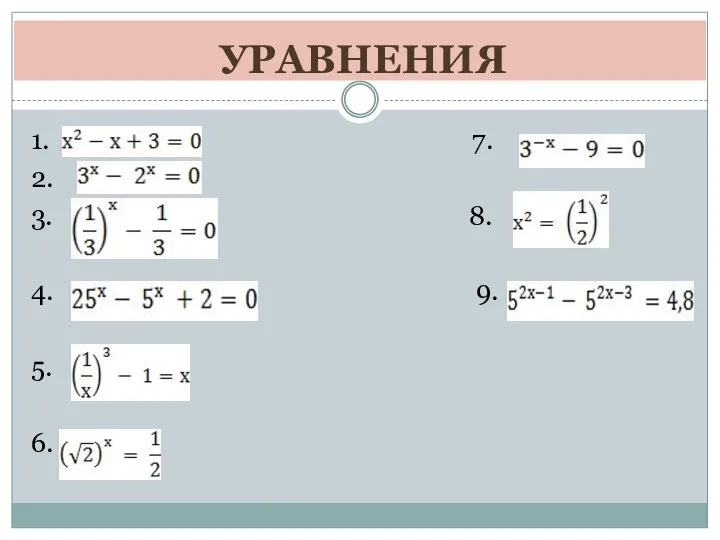 Решение показателей уравнений
Решение показателей уравнений Элементы нелинейного функционального анализа. Глава 1. Дифференциальное исчисление в нормированных пространствах
Элементы нелинейного функционального анализа. Глава 1. Дифференциальное исчисление в нормированных пространствах Письменное умножение двузначных и трехзначных чисел на однозначное число
Письменное умножение двузначных и трехзначных чисел на однозначное число Презентация на тему УМНОЖЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
Презентация на тему УМНОЖЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ  Интерактивный тренажёр Повторяем величины с домовёнком
Интерактивный тренажёр Повторяем величины с домовёнком Координаты вектора
Координаты вектора Введение в математическую логику и теорию множеств
Введение в математическую логику и теорию множеств Презентация на тему Виды алгоритмов
Презентация на тему Виды алгоритмов  Вычитание чисел. Решение уравнений
Вычитание чисел. Решение уравнений Показательные неравенства
Показательные неравенства Итоги главы 4
Итоги главы 4 Линейная алгебра
Линейная алгебра Геометрические ребусы
Геометрические ребусы Процентное отношение
Процентное отношение Презентация на тему Математический диктант 2 класс
Презентация на тему Математический диктант 2 класс  Окружность. Комбинации с окружностью. ЕГЭ
Окружность. Комбинации с окружностью. ЕГЭ Метрология как наука
Метрология как наука Презентация на тему Как читать графики
Презентация на тему Как читать графики  Веб – квест для учащихся 11 класса. Задачи по теме Производная
Веб – квест для учащихся 11 класса. Задачи по теме Производная Веселые примеры
Веселые примеры Решение задач
Решение задач Подготовка к экзамену по математике
Подготовка к экзамену по математике ОГЭ 2022 Математика. Вариант 15
ОГЭ 2022 Математика. Вариант 15 Системы уравнений
Системы уравнений Тема урока: «Аксиомы стереометрии и их следствия. Решение задач»
Тема урока: «Аксиомы стереометрии и их следствия. Решение задач» Перебор, часть 2
Перебор, часть 2 Столько же, на 2 больше. 1 класс
Столько же, на 2 больше. 1 класс Прямо-пропорциональные величины
Прямо-пропорциональные величины