Содержание
- 2. Распределение непрерывных случайных величин Случайна величина Х называется непрерывной, если невозможно перечислить все ее значения Например,
- 3. 17. Распределение непрерывных случайных величин Вместо вероятности того, что случайная величина Х примет значение, равное х,
- 4. Известно, что студент приходит на занятия в случайный момент времени в интервале от 8.00 до 9.00.
- 5. 8.00 9.00 x событие если
- 6. если
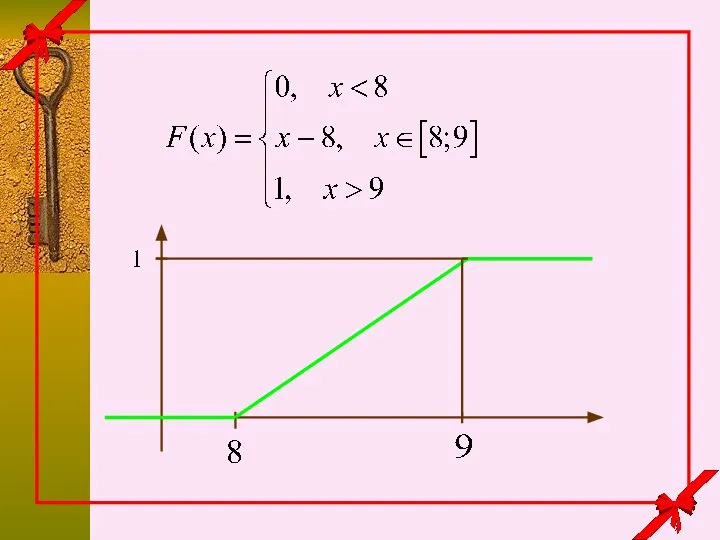
- 7. если если
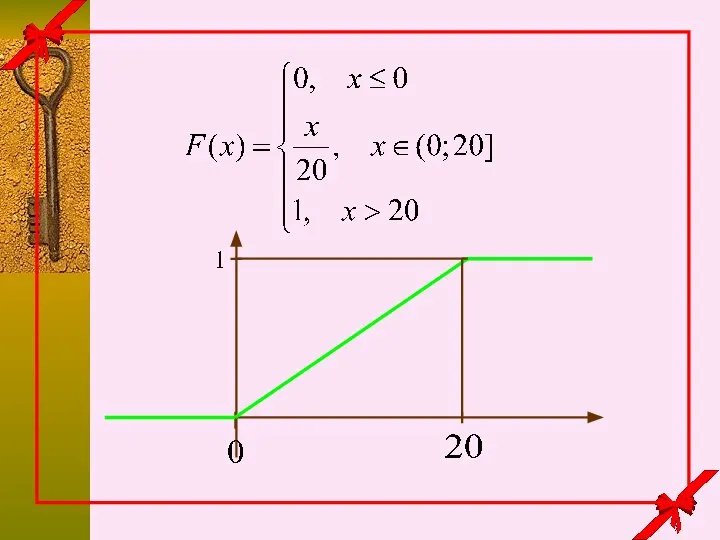
- 10. Автобусы ходят с интервалом 20 минут. Пассажир подходит к остановке в случайный момент времени. Пусть Х
- 11. 0 20 x событие если
- 12. если
- 13. если если
- 16. 1 Функция распределения является неубывающей функцией. Для любых выполнено свойства функции распределения
- 17. 2 На минус бесконечности функция распределения равна нулю:
- 18. 3 На плюс бесконечности функция распределения равна единице:
- 19. ВЕРОЯТНОСТЬ ПОПАДАНИЯ СВ НА ЗАДАННЫЙ ИНТЕРВАЛ 4
- 20. 5
- 21. Пример Используя функцию распределения величины X – Время прихода студента на лекцию, найти вероятность того, что
- 22. Рассмотрим непрерывную случайную величину Х с функцией распределения F(x). Вычислим вероятность попадания этой случайной величины на
- 23. Рассмотрим непрерывную случайную величину Х с функцией распределения F(x). Вычислим вероятность попадания этой случайной величины на
- 24. По определению производной этот предел равен производной функции F(x) : = Функция f(x), равная производной от
- 25. При малых величина приближенно показывает вероятность попадания в
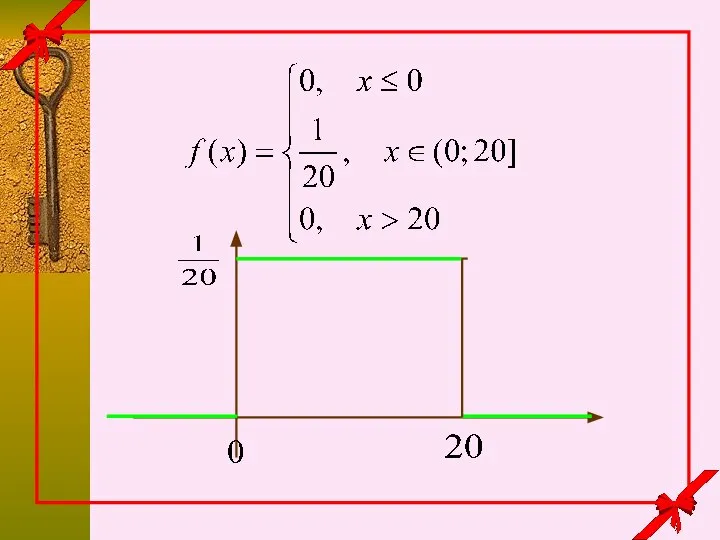
- 26. Пример Дана функция распределения. Найти плотность распределения
- 27. Пример Дана функция распределения.
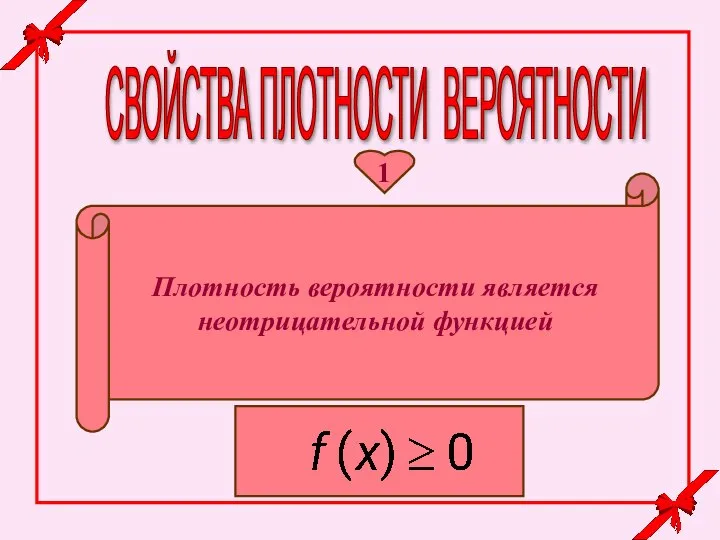
- 29. 1 Плотность вероятности является неотрицательной функцией СВОЙСТВА ПЛОТНОСТИ ВЕРОЯТНОСТИ
- 30. Вероятность попадания случайной величины в отрезок 2
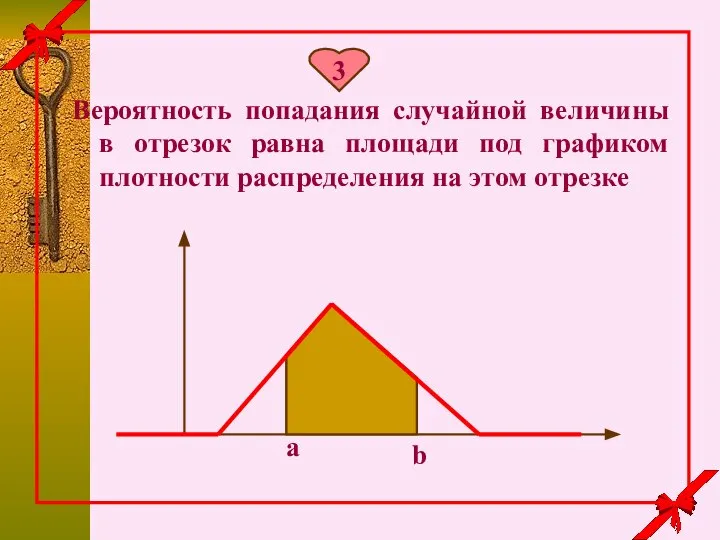
- 31. Вероятность попадания случайной величины в отрезок равна площади под графиком плотности распределения на этом отрезке 3
- 33. Скачать презентацию




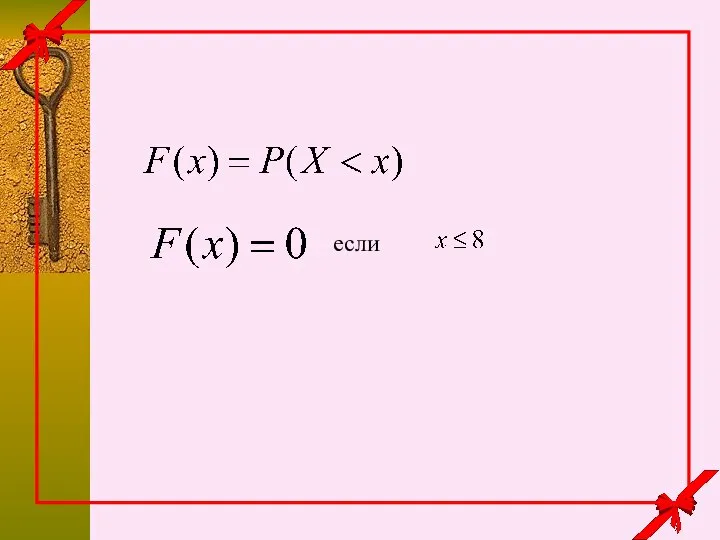
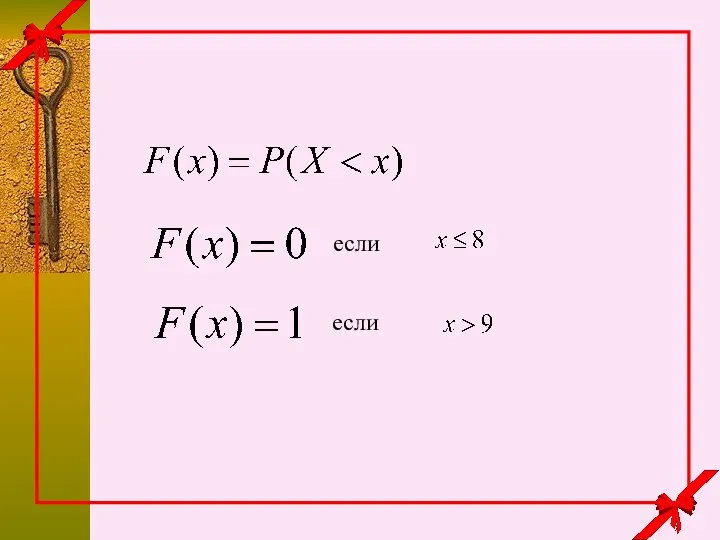
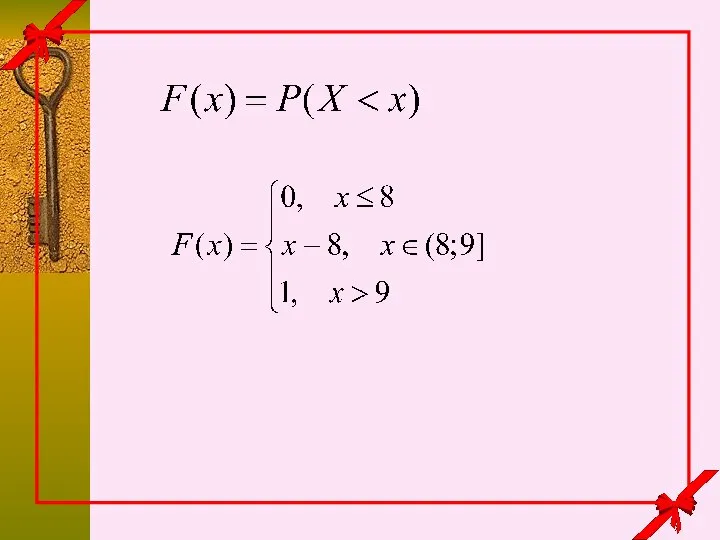




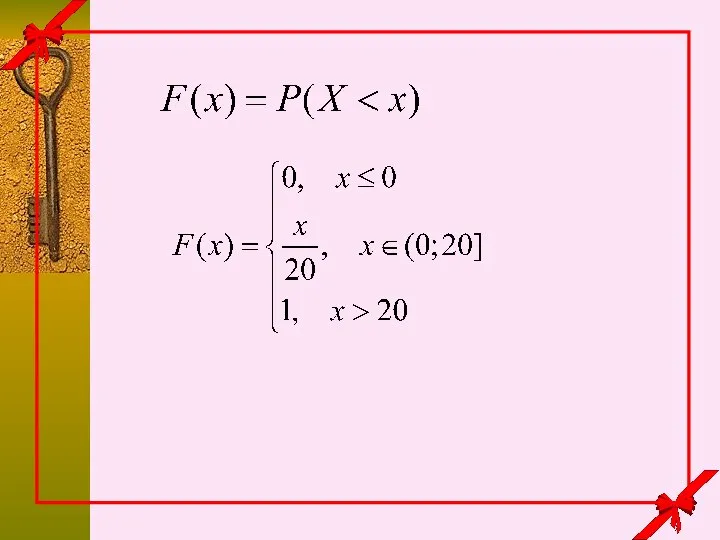




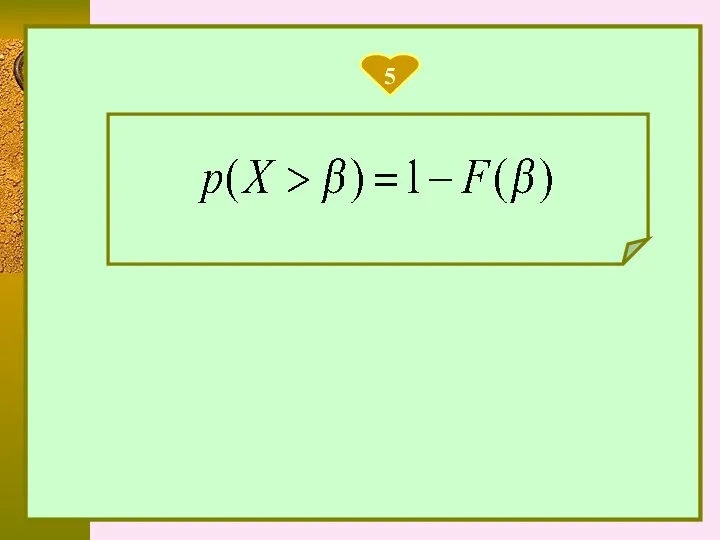








 Презентация по математике "Ломаные числа" -
Презентация по математике "Ломаные числа" -  Умножение числа 0 и на число 0 Умножение числа 1 и на число 1
Умножение числа 0 и на число 0 Умножение числа 1 и на число 1 Методы корреляционно-регрессионного анализа фондового рынка
Методы корреляционно-регрессионного анализа фондового рынка Статистическая проверка статистических гипотез
Статистическая проверка статистических гипотез Математика и техника. Их связь и значение
Математика и техника. Их связь и значение Групповое задание
Групповое задание Коррекция нелинейных систем
Коррекция нелинейных систем Перемещение тела на плоскости (задача)
Перемещение тела на плоскости (задача) Теорема Пифагора
Теорема Пифагора Таблица умножения на 2
Таблица умножения на 2 Повторение и закрепление. Итоговое повторение за год. 4 класс
Повторение и закрепление. Итоговое повторение за год. 4 класс Прямоугольник. Ромб. Квадрат
Прямоугольник. Ромб. Квадрат Что такое разложение на множители и зачем оно нужно
Что такое разложение на множители и зачем оно нужно Гомотетия. Подобие фигур
Гомотетия. Подобие фигур Элементы математической логики
Элементы математической логики История возникновения науки геометрии
История возникновения науки геометрии Презентация на тему Окружность ее центр и радиус
Презентация на тему Окружность ее центр и радиус  Геометрические тела. 9 класс
Геометрические тела. 9 класс Формирование регулятивных УУД у младших школьников при изучении геометрического материала
Формирование регулятивных УУД у младших школьников при изучении геометрического материала Стандартизация в различных сферах. Сущность стандартизации
Стандартизация в различных сферах. Сущность стандартизации Без знаний дробей никто не может признаваться знающим арифметику
Без знаний дробей никто не может признаваться знающим арифметику Признак перпендикулярности плоскостей
Признак перпендикулярности плоскостей Kоординатная плоскость
Kоординатная плоскость Средние величины
Средние величины Математика. Роль математики в жизни людей и общества
Математика. Роль математики в жизни людей и общества Действия с натуральными числами. Сложение и вычитание
Действия с натуральными числами. Сложение и вычитание Решение уравнений
Решение уравнений Презентация на тему Римские цифры (3 класс)
Презентация на тему Римские цифры (3 класс)