Матрицы и определители. Основные понятия и определения. Понятие матрицы

Основные понятия и определения

Понятие матрицы
Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк и n столбцов.
Обозначение матриц: A, B, C, …
Числа, составляющие матрицу, называются элементами матрицы.
Обозначение элементов:
где i – номер строки, j – номер столбца

Запись матриц
В общем виде
В сокращенной форме

Пример

Виды матриц
Определение: Матрица любого размера называется нулевой или нуль-матрицей, если все ее элементы равны нулю.
Обозначение: О
Пример:

Виды матриц
Матрица, размерности:
1×n называется матрицей-строкой или вектором-строкой
m×1 называется матрицей-столбцом или вектором-столбцом

Виды матриц
Матрица размерности n×n называется квадратной порядка n
Пример
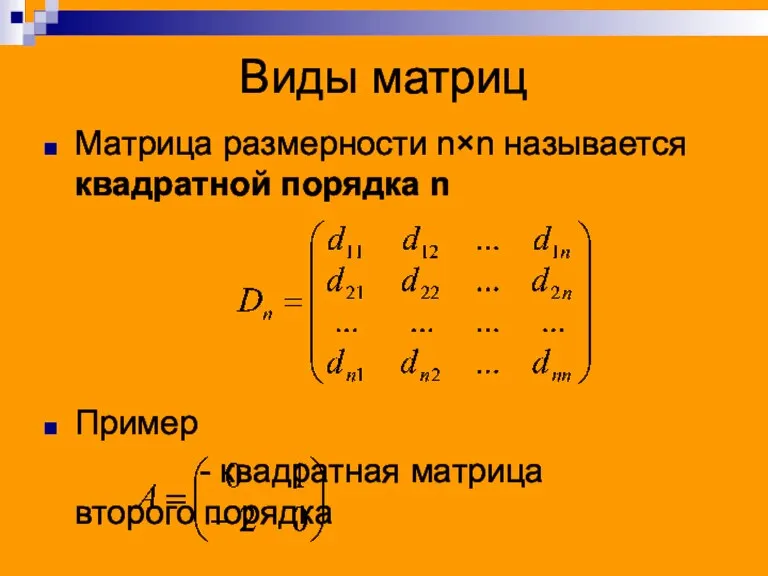
- квадратная матрица второго порядка

Диагональ матрицы
Элементы матрицы, у которых номер столбца равен номеру строки (i=j), называются диагональными и составляют главную диагональ матрицы.
Сумма элементов главной диагонали квадратной матрицы называется её следом. Обозначается trA.

Виды квадратных матриц
Квадратная матрица, у которой все недиагональные элементы равны нулю, называется диагональной матрицей.
Пример:
- диагональная матрица
второго порядка

Виды квадратных матриц
Если у диагональной матрицы порядка n все диагональные элементы равны 1, матрица называется единичной порядка n.
Обозначение En
Пример
- единичная матрица
третьего порядка

Виды матриц

Операции
над матрицами

Операции над матрицами
Умножение матрицы на число
Сложение матриц
Вычитание матриц
Умножение матриц
Возведение в степень
Транспонирование матрицы

Умножение матрицы на число
Выполнимо для любых матриц и любых чисел
Производится поэлементно
Правило:
Пример:

Сложение матриц
Выполнимо только для матриц одинаковой размерности
Производится поэлементно
Правило:
Пример:

Вычитание матриц
Выполнимо только для матриц одинаковой размерности
Производится поэлементно
Правило:
или
Пример:

Умножение матриц
Выполнимо если число столбцов первого множителя равно числу строк второго
Правило:
Примеры:

Возведение в степень
Выполнимо для квадратных матриц
Правила:
Пример:

Транспонирование
Выполнимо для любой матрицы
Обозначение: АТ или А'
Правило: поменять строки на столбцы с сохранением порядка.
Пример:

Определители квадратных матриц

Определитель матрицы
Любой квадратной матрице ставится в соответствие по определенному закону некоторое число, называемое определителем или детерминантом.
Обозначение:
det A или |А| или ∆А или ∆n или ∆
Определитель матрицы – это число.
Определитель существует только для квадратных матриц.

Определитель второго порядка
Определяется формулой:
Пример:

Определитель третьего порядка
Определяется формулой

Определитель третьего порядка
Знаки произведений определяются с помощью правила треугольников или правила Саррюса:

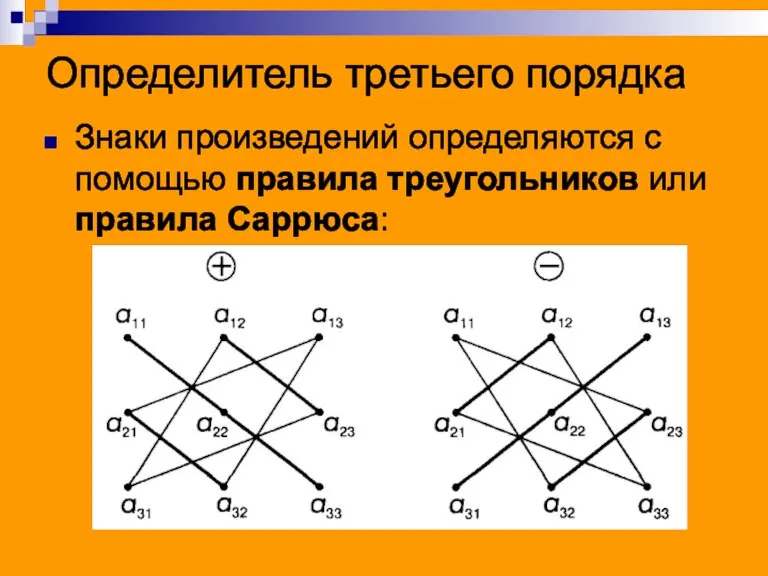
Определитель n-го порядка
Определителем матрицы А n-го порядка называется алгебраическая сумма n! произведений n-го порядка элементов этой матрицы, причем в каждое произведение входит по одному элементу из каждой строки и каждого столбца данной матрицы

Минор
Рассмотрим квадратную матрицу Аn
Минором называется определитель (n-1)-го порядка, полученный вычеркиваем из матрицы А i-й строки и j-го столбца.
Пример:

Алгебраическое дополнение
Алгебраическим дополнением называется минор , взятый со знаком , т.е.
Пример
Матрица, составленная из алгебраических дополнений элементов матрицы А, называется присоединенной матрицей и обозначается

Теорема Лапласа
Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
- разложение определителя по элементам i-й строки
Используется для вычисления определителей порядка выше третьего.

Теорема Лапласа (пример)
Вычислить
Решение:

Свойства определителей
При транспонировании ∆ не меняется.
При перестановке двух строк ∆ меняет знак.
∆=0 если:
содержит нулевую строку (столбец);
содержит две одинаковые строки;
содержит две пропорциональные строки.
Если все элементы строки умножить на число λ, то ∆ увеличится в λ раз; общий множитель строки можно вынести за знак ∆.
Если к элементам строки прибавить элементы другой строки, умноженной на число ≠0, то ∆ не меняется.

Свойства определителей
Определитель треугольной матрицы равен произведению ее диагональных элементов.
Определитель диагональной матрицы равен произведению ее диагональных элементов

Способы вычисления определителей
Перебором всевозможных произведений (по определению);
Разложением по строке или столбцу (по теореме Лапласа);
С использованием свойств определителей;
Сочетание способов.

Обратная матрица
Обозначение: А-1–обратная для матрицы А
Определение: Матрицей А-1, обратной к данной квадратной матрице А, называется такая, что выполняется равенство:
А-1∙А = А∙ А-1 = Е.
Пример: -обратна матрице ,
т.к.

Обратимость матрицы
Если определитель квадратной матрицы равен нулю (∆А=0), матрица называется вырожденной.
Если определитель отличен от нуля (∆А≠0), матрица называется невырожденной.
Критерий обратимости матрицы:
А имеет обратную ↔ А – невырожденная
Обратную матрицу можно найти по формуле:

Алгоритм нахождения
обратной матрицы
Вычислить ∆А. Если ∆А=0, то А-1 не существует.
Если ∆А≠0, найти алгебраические дополнения всех элементов. Составить
Транспонировать матрицу
Выполнить умножение на
Выполнить проверку равенства А-1∙А = Е.

Нахождение обратной матрицы (пример)
Найти матрицу, обратную к
Решение:
1. ∆А = -1∙1 - 2∙0 = -1 ≠0 → А-1 существует.
2.
Итак,
3.

Нахождение обратной матрицы (пример)
4.
5. Проверка:
Ответ:

Ранг матрицы
Определение: Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы.
Обозначение: rang A или r(A).
Ранг матрицы показывает число ее линейно независимых строк (столбцов).