Содержание
- 2. Целочисленные задачи линейного программирования Задача линейного программирования, в которой требуется, чтобы все переменные были целыми, называется
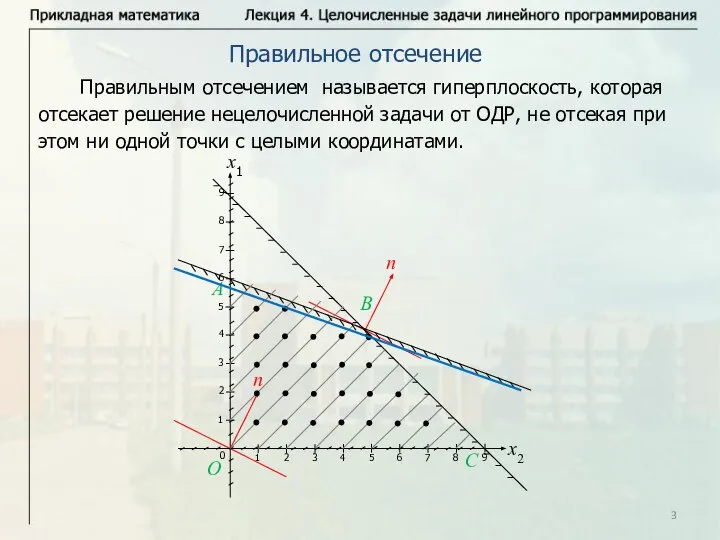
- 3. Правильное отсечение x1 Правильным отсечением называется гиперплоскость, которая отсекает решение нецелочисленной задачи от ОДР, не отсекая
- 4. Метод отсечений Метод отсечений был разработан в конце 1950-х годов Гомори для решения целочисленных линейных задач
- 5. Отсечение Гомори Если получена симплекс-таблица нецелочисленного решения, то по отсечению Гомори определяется строка вида: , где
- 6. Задача о раскрое Имеются бревна длиной 3 метра. Из них требуется сделать не менее 50 заготовок
- 7. Задача о раскрое Обозначим - количество бревен, распиливаемых -м способом, Тогда задача примет вид
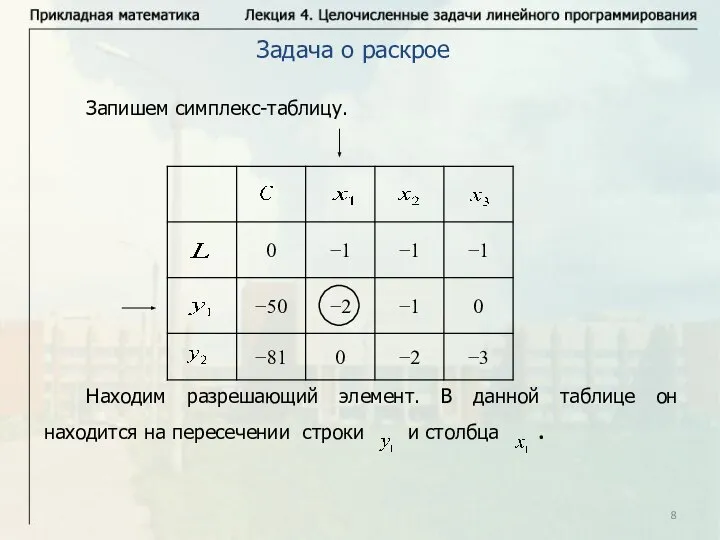
- 8. Запишем симплекс-таблицу. Находим разрешающий элемент. В данной таблице он находится на пересечении строки и столбца .
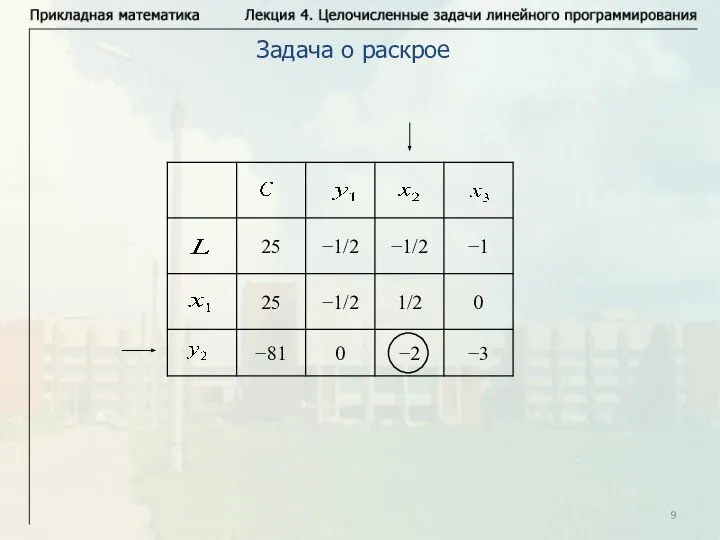
- 9. Задача о раскрое
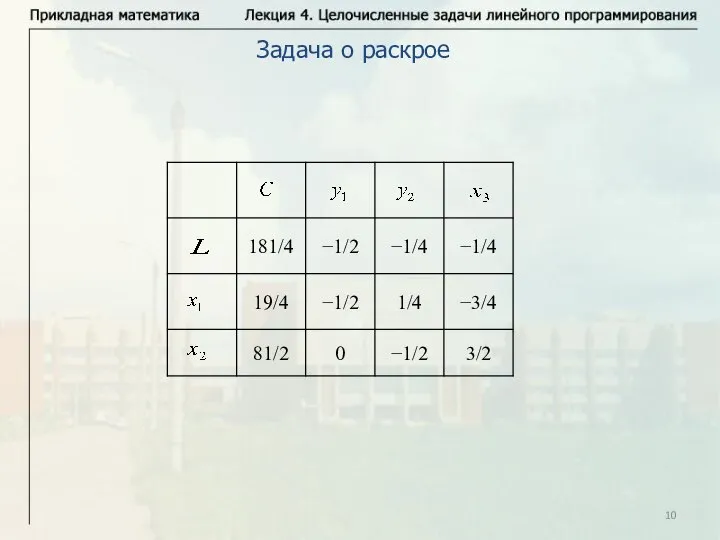
- 10. Задача о раскрое
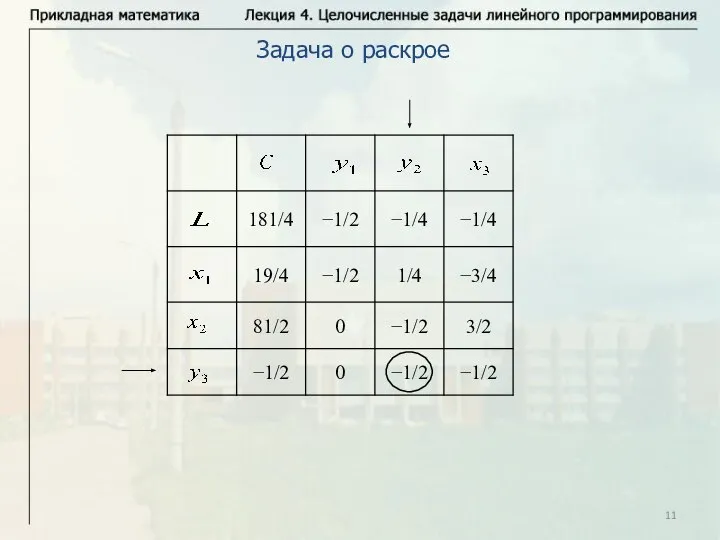
- 11. Задача о раскрое
- 12. Задача о раскрое
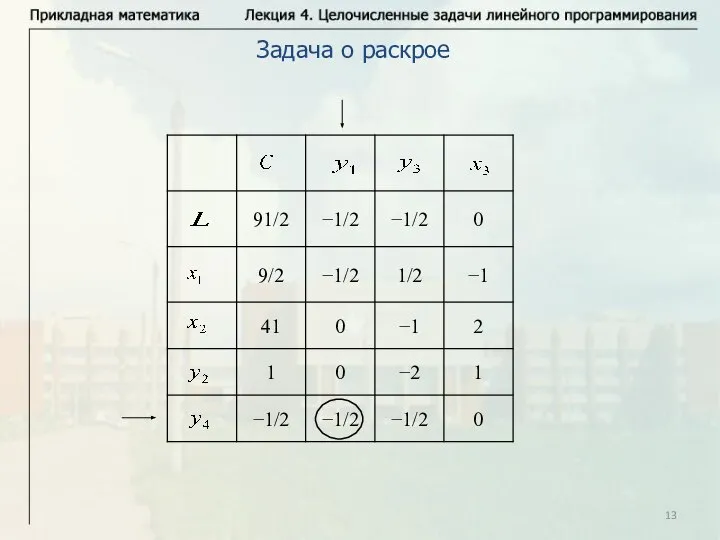
- 13. Задача о раскрое
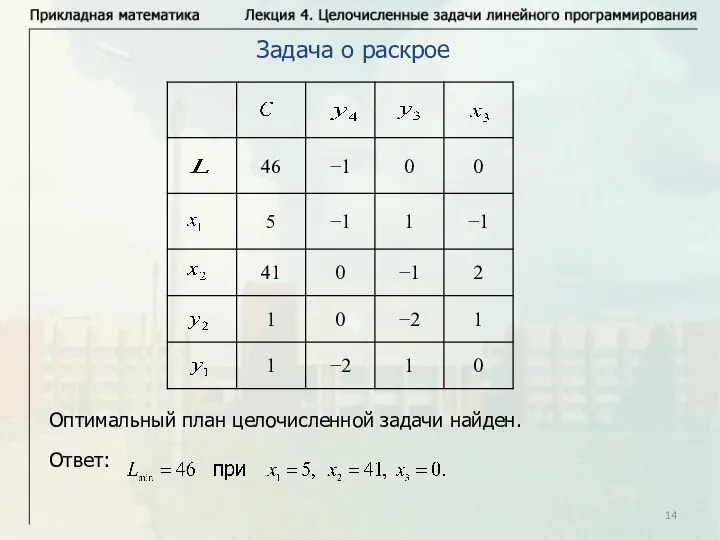
- 14. Задача о раскрое Оптимальный план целочисленной задачи найден. Ответ:
- 15. Найдем другие решения этой задачи. Так как в первой строке L симплекс-таблицы при и коэффициенты равные
- 16. Следовательно, задача имеет 6 решений. 1) при решение 2) при решение 3) при решение 4) при
- 17. Можно принять во внимание дополнительные соображения по поводу лучшего решения: Минимальные отходы. Так как второй способ
- 18. Суть данного метода в том, что если в оптимальном решении дробное, то из ОДР исключается множество
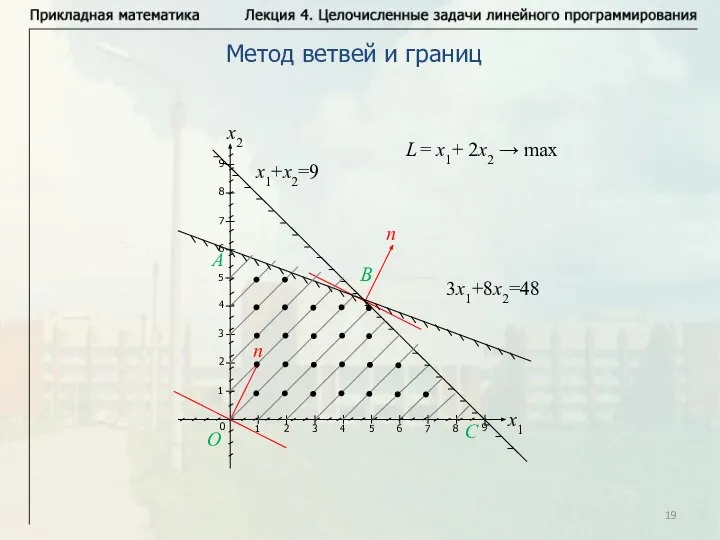
- 19. Метод ветвей и границ L = x1+ 2x2 → max
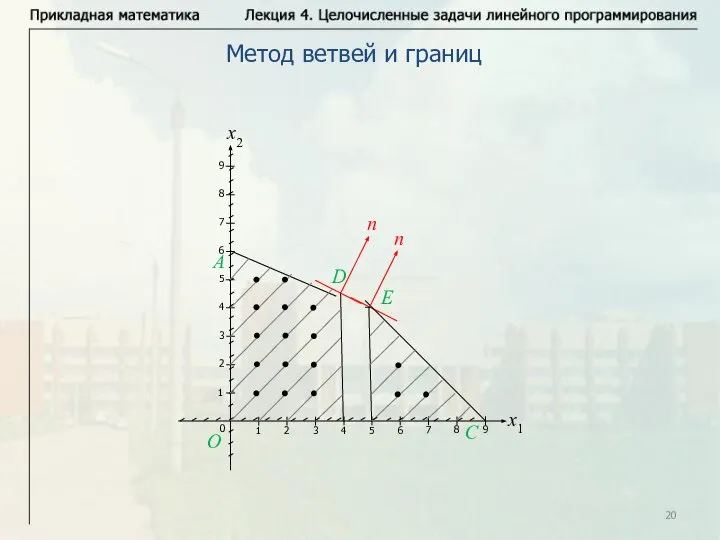
- 20. Метод ветвей и границ
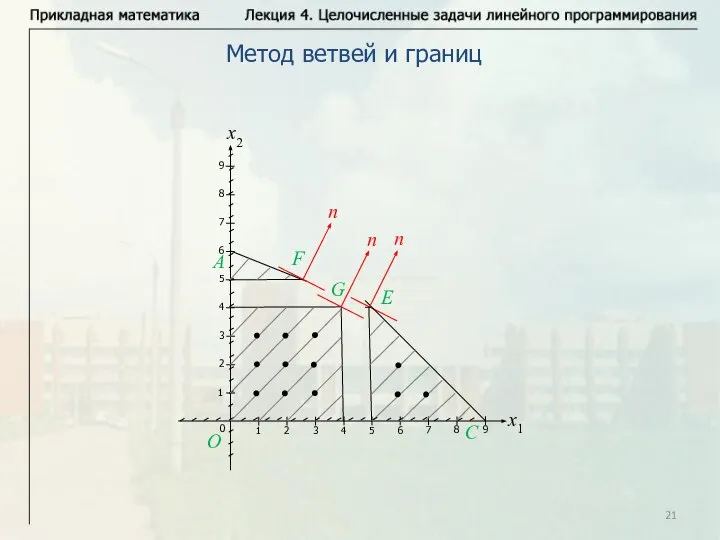
- 21. Метод ветвей и границ
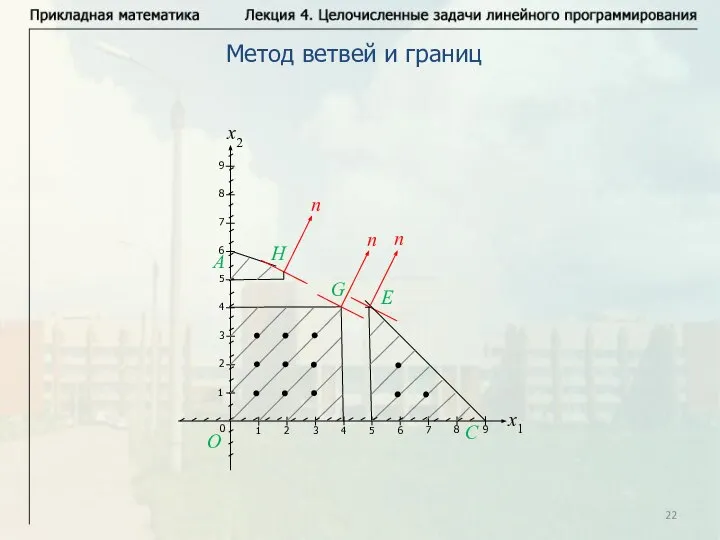
- 22. Метод ветвей и границ
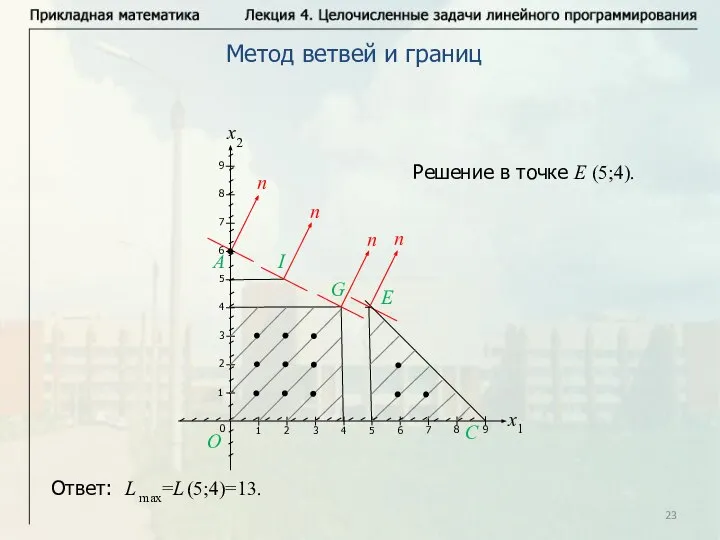
- 23. Метод ветвей и границ Решение в точке Е (5;4). Ответ: L max=L (5;4)=13.
- 24. 1. Целочисленной задачей линейного программирования называется задача линейного программирования, в которой дополнительно требуются, чтобы... все коэффициенты
- 25. 2. Целой частью числа x называется… максимальное целое число, которое не меньше x; максимальное целое число,
- 26. 3. В методе отсечений Гомори в симплекс-таблицу оптимального нецелочисленного решения добавляется строка, для которой... коэффициент в
- 28. Скачать презентацию













 Путешествие в город Дробей на проспект Умножения. 6 класс
Путешествие в город Дробей на проспект Умножения. 6 класс Действительный анализ. Теорема Лебега (примеры). Измеримые множества
Действительный анализ. Теорема Лебега (примеры). Измеримые множества Как умножали египтяне
Как умножали египтяне Площадь многоугольника
Площадь многоугольника Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства
Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства Полигон частот в математической статистике
Полигон частот в математической статистике Лінейныя ўраўненні з адной зменнай
Лінейныя ўраўненні з адной зменнай Расчёт скорости официанта от кассы до столика
Расчёт скорости официанта от кассы до столика Объём тела
Объём тела Теорема о плоскости, касательной к шару
Теорема о плоскости, касательной к шару Площадь круга и секторов
Площадь круга и секторов Куб
Куб Корень степени n
Корень степени n Построение биссектрисы угла. Билеты
Построение биссектрисы угла. Билеты Урок математики 20.09
Урок математики 20.09 Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ  Занимательные математические задания
Занимательные математические задания Сравнение групп предметов. Свойства предметов (1 класс)
Сравнение групп предметов. Свойства предметов (1 класс) Математическая модель колонны многокомпонентной ректификации. Лекция 9
Математическая модель колонны многокомпонентной ректификации. Лекция 9 Производная в заданиях уровня В. ЕГЭ
Производная в заданиях уровня В. ЕГЭ Неопределенный интеграл
Неопределенный интеграл Презентация на тему Простые числа
Презентация на тему Простые числа  История г. Колпашева в примерах и задачах
История г. Колпашева в примерах и задачах Сочетания. Свойства сочетаний. Бином Ньютона
Сочетания. Свойства сочетаний. Бином Ньютона Основные понятия теории вероятностей
Основные понятия теории вероятностей Возрастание и убывание функций. Экстремумы
Возрастание и убывание функций. Экстремумы Памятка по оформлению краткой записи к задачам (1 класс)
Памятка по оформлению краткой записи к задачам (1 класс)