Слайд 2Утверждения
Общие Частные
Все граждане России Петров имеет право на
имеют право на образование.
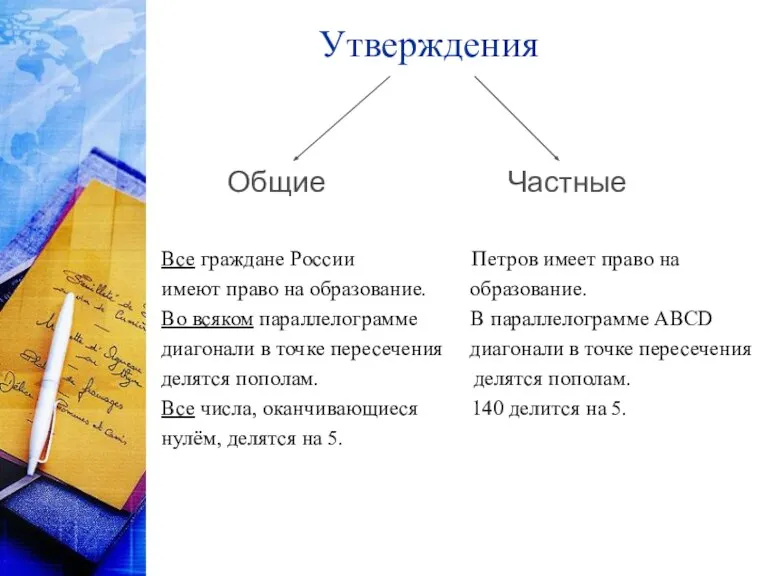
образование.
Во всяком параллелограмме В параллелограмме ABCD
диагонали в точке пересечения диагонали в точке пересечения
делятся пополам. делятся пополам.
Все числа, оканчивающиеся 140 делится на 5.
нулём, делятся на 5.
Слайд 3Дедукция –
переход от общих утверждений к частным.
Пример.
Все граждане России имеют право

на образование.
Петров – гражданин России.
Петров имеет право на образование.
Слайд 4Индукция –
переход от частных утверждений к общим.
Пример.
140 делится на 5.
Все числа,

оканчивающиеся нулём, делятся на 5.
140 делится на 5.
Все трёхзначные числа делятся на 5.
Слайд 5,
Знаменитый математик XVII в. П.Ферма проверив, что числа
простые, сделал по индукции

предположение, что для всех n=1,2,3,… числа вида
простые.
Слайд 6В XVIII веке Л.Эйлер нашел, что при n=5
составное число.

Слайд 7Индукция
Полная Неполная
Требуется установить, что каждое натуральное чётное число n в

пределах 4< n < 20 представимо в виде суммы двух простых чисел.
Для этого возьмём все такие числа и выпишем соответствующие разложения:
4=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5; 14=7+7; 16=11+5; 18=13+5; 20=13+7.
Эти девять равенств показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.
Слайд 8Задача.
Перед нами последовательность нечетных чисел натурального ряда.
1,3,5,7,9,11,13…
Чему равна сумма n первых

членов этой последовательности?
Слайд 9Решение:
Рассмотрим частные случаи:
1=1
1+3=4
1+3+5=9
1+3+5+7=16
1+3+5+7+9=25 …
Общий вывод: 1+3+5+…+(2n-1)=n2.
Как же узнать, справедливо ли

это утверждение вообще?
Слайд 10Принцип математической индукции
Утверждение P(n) справедливо для всякого натурального n, если:
Оно справедливо

для n=1 или для наименьшего из натуральных чисел при котором закономерность имеет смысл.
Из справедливости утверждения для какого либо произвольного натурально n=k следует его справедливость для n=k+1.
Слайд 11Алгоритм доказательства методом математической индукции
Проверяют справедливость гипотезы для наименьшего из натуральных чисел

при котором гипотеза имеет смысл (базис индукции).
Сделав предположение, что гипотеза верна для некоторого значения k, стремятся доказать справедливость ее для k+1 (индукционный шаг).
Если такое доказательство удалось довести до конца, то, на основе принципа математической индукции можно утверждать, что высказанная гипотеза справедлива для любого натурального числа n.
Слайд 12Суть доказательства
методом математической индукции:
базис проверить верность утверждения при n= 1
индукционный

шаг
- допустить, что утверждение верно при n= k
- доказать, что утверждение верно при n= k+1
Докажите, что 1+3+5+…+(2n-1)=n2.
Слайд 13Доказать, что 1+3+5+…+(2n-1)=n2.
Доказательство:
Имеем n=1=12. Следовательно, утверждение верно при n=1.
Пусть k-любое натуральное число

и пусть утверждение справедливо для n=k, т.е. 1+3+5+…+(2k-1)=k2.
Докажем, что тогда утверждение справедливо и для следующего натурального числа n=k+1, т.е. что 1+3+5+…+(2k+1)=(k+1)2.
1+3+5+…+(2k-1)+(2k+1)=k2+(2k+1)=(k+1)2.
Итак, утверждение 1+3+5+…+(2n-1)=n2 истинно для любого натурального n.
Слайд 15Доказательство:
1. Проверим верность утверждения при n=2.
Следовательно, утверждение верно при n=2.
2.

Пусть утверждение справедливо для n=k>2, т.е.
Докажем истинность утверждения для n=k+1, т.е. что
Итак, утверждение истинно для любого натурального n≥2.
Слайд 16Задача
Доказать, что для любого натурального числа n истинно утверждение

Слайд 17Задача
Доказать, что сумма n первых чисел натурального ряда равна

Слайд 18Метод математической индукции
позволяет в поисках общего закона испытывать возникающие при этом

гипотезы, отбрасывать ложные и утверждать истинные.
Слайд 19 «Понимание и умение правильно применять принцип математической индукции, является хорошим критерием логической

зрелости, которая совершенно необходима математику».
А.Н. Колмогоров


















 Приемы решения целых уравнений
Приемы решения целых уравнений Арксинус, арккосинус, арктангенс и арккотангенс
Арксинус, арккосинус, арктангенс и арккотангенс Проверочная логарифмические неравенства и уравнение
Проверочная логарифмические неравенства и уравнение Перевод единиц измерений, сравнение величин, запись чисел в стандартном виде
Перевод единиц измерений, сравнение величин, запись чисел в стандартном виде Презентация на тему Путешествие в страну Занимательной математики (1 класс)
Презентация на тему Путешествие в страну Занимательной математики (1 класс)  Своя игра по математике
Своя игра по математике Свойства степени с целым отрицательным показателем
Свойства степени с целым отрицательным показателем Отбор корней в тригонометрическом уравнении
Отбор корней в тригонометрическом уравнении Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями Определение определённого интеграла (Лекция 2)
Определение определённого интеграла (Лекция 2) Игра-тренажер Изучаем время
Игра-тренажер Изучаем время Лишь знанием движется век, Лишь знанием жив человек!
Лишь знанием движется век, Лишь знанием жив человек! Задания из открытого банка ЕГЭ
Задания из открытого банка ЕГЭ Тестовые задания в формате ГИА. К уроку алгебры в 8 классе
Тестовые задания в формате ГИА. К уроку алгебры в 8 классе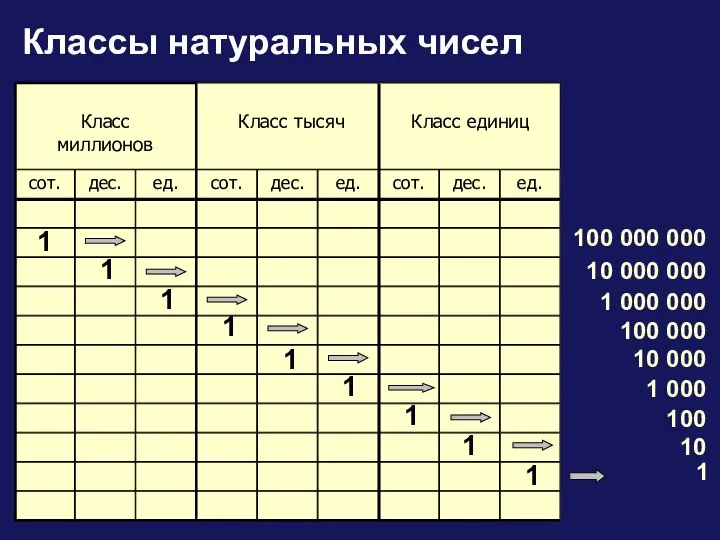 Классы натуральных чисел
Классы натуральных чисел Дроби
Дроби Тест по теме Цилиндр
Тест по теме Цилиндр Измерение и построение углов
Измерение и построение углов Расстояние между точками с заданными координатами. Координаты середины отрезка
Расстояние между точками с заданными координатами. Координаты середины отрезка Соотношение между сторонами и углами треугольника
Соотношение между сторонами и углами треугольника РўР’РёРњРЎ_Лекция 4_Дискретные СЃРучайные РІРµРичины
РўР’РёРњРЎ_Лекция 4_Дискретные СЃРучайные РІРµРичины Треугольники. ЕГЭ
Треугольники. ЕГЭ Приведение к каноническому виду уравнений параболического типа
Приведение к каноническому виду уравнений параболического типа Группировка слагаемых. Сочетательное свойство сложения
Группировка слагаемых. Сочетательное свойство сложения Random module methods. Test
Random module methods. Test Умножение и деление натуральных чисел
Умножение и деление натуральных чисел График квадратичной функции
График квадратичной функции Презентация по математике "Дроби в Древнем Египте" -
Презентация по математике "Дроби в Древнем Египте" -