Слайд 2ЦЕЛИ ПРОЕКТА:
Познакомиться с методами решения возвратных уравнений.
Совершенствовать навыки решения уравнений.
Овладеть способами сбора

и хранения информации (создать презентацию)
Слайд 3ВОЗВРАТНЫЕ УРАВНЕНИЯ
Возвратное уравнение – алгебраическое уравнение
а0хn + a1xn – 1 + …

+ an – 1x +an=0, в котором ак = an – k,
где k = 0, 1, 2 …n, причем, а ≠ 0.
Задачу нахождения корней возвратного уравнения сводят к задаче нахождения решений алгебраического уравнения меньшей степени. Термин возвратные уравнения был введён Л. Эйлером.
Слайд 4Уравнения, у которых коэффициенты членов, равноудаленных от «начала» и «конца» уравнения, равны

между собой, называются симметричными.
6х4-35х3+62х2-35х+6=0
Симметричные уравнения четвертой степени.
1)Если m = 1, то это симметричное уравнение первого рода, имеющее вид
ax4 + bx3 + cx2 + bx + a = 0 и решающееся новой подстановкой y =
2) Если m = -1, то это симметричное уравнение второго рода, имеющее вид
ax4 + bx3 + cx2 - bx + a = 0 и решающееся новой подстановкой y =
Слайд 11
5Х3 + 21Х2+21Х +5=0
СИММЕТРИЧЕСКОЕ УРАВНЕНИЕ











 Сравнение отрезков и углов геометрических фигур
Сравнение отрезков и углов геометрических фигур Числовые промежутки
Числовые промежутки Решение задач с помощью уравнений. Устные вычисления
Решение задач с помощью уравнений. Устные вычисления Золотое сечение
Золотое сечение Решение задач разными арифметическими способами
Решение задач разными арифметическими способами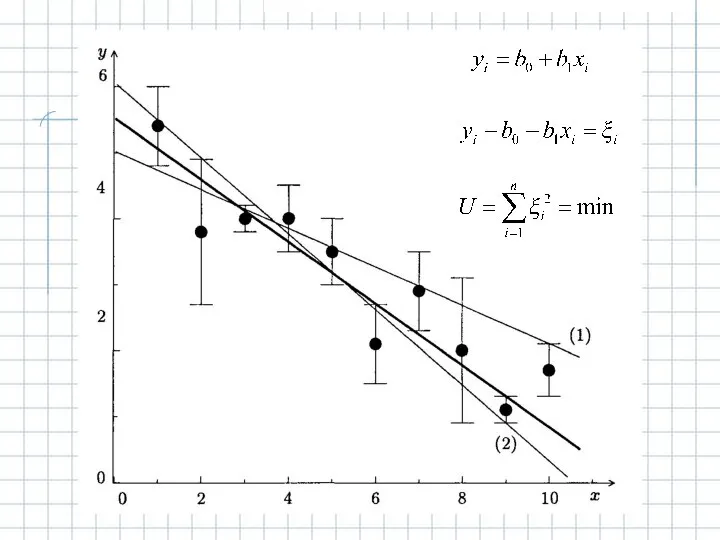 Расчет коэффициентов регрессии (МНК)
Расчет коэффициентов регрессии (МНК) Презентация на тему Сложение и вычитание смешанных чисел
Презентация на тему Сложение и вычитание смешанных чисел  Решение тригонометрических уравнений
Решение тригонометрических уравнений 1. Метрология
1. Метрология Скользящее среднее
Скользящее среднее Влияние личности педагога на формирование ключевых компетентностей и повышения познавательной активности обучающихся
Влияние личности педагога на формирование ключевых компетентностей и повышения познавательной активности обучающихся Индивидуальные задания. Урок 15
Индивидуальные задания. Урок 15 Презентация на тему Математика ЕГЭ 2012
Презентация на тему Математика ЕГЭ 2012  Властивості задачі лінійного програмування
Властивості задачі лінійного програмування Факультативное занятие. Лабиринт. 6 класс
Факультативное занятие. Лабиринт. 6 класс Презентация на тему Вектор
Презентация на тему Вектор  Преобразование обыкновенных дробей в десятичные и десятичных в обыкновенные
Преобразование обыкновенных дробей в десятичные и десятичных в обыкновенные Окружность
Окружность Что? Где? Когда?
Что? Где? Когда? Презентация на тему НАХОЖДЕНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ
Презентация на тему НАХОЖДЕНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ  Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ  Комплексные числа
Комплексные числа Пересечение линии и поверхности. Позиционные задачи. (Лекция 8.2)
Пересечение линии и поверхности. Позиционные задачи. (Лекция 8.2) Комбинаторика. Комбинаторные объекты
Комбинаторика. Комбинаторные объекты Число семь. Цифра 7
Число семь. Цифра 7 Сан. Числительное
Сан. Числительное Логарифмические неравенства
Логарифмические неравенства Основы математической статистики
Основы математической статистики