Слайд 2Тригонометрические функции.
Тригонометрические функции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольниках и выражали

зависимости сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла (дуги) в круге).
Слайд 3Содержание:
Историческая справка
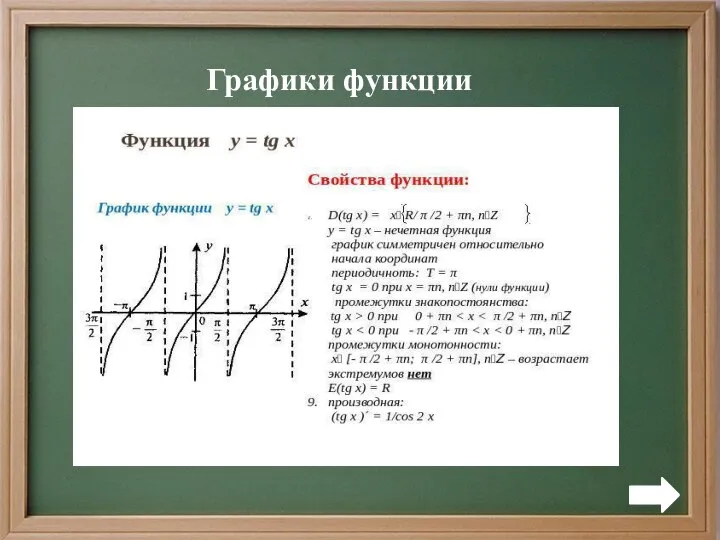
Графики функций
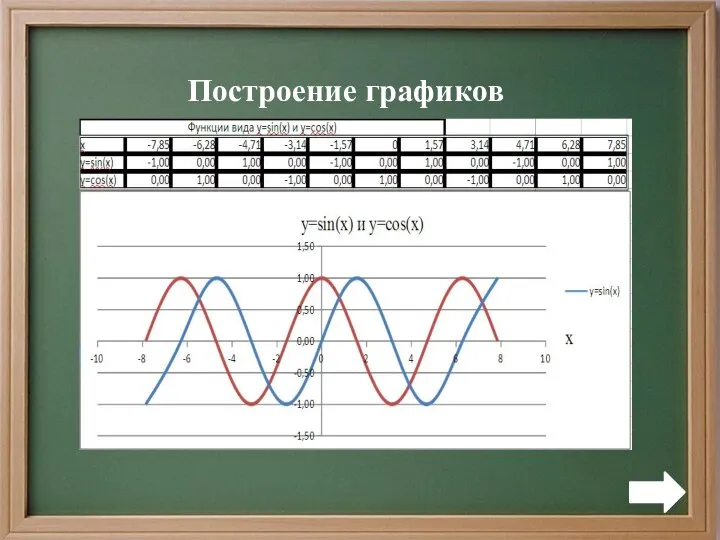
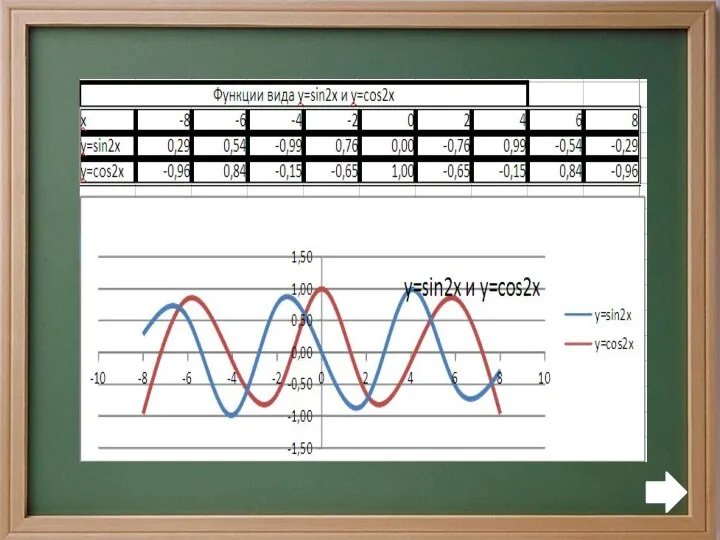
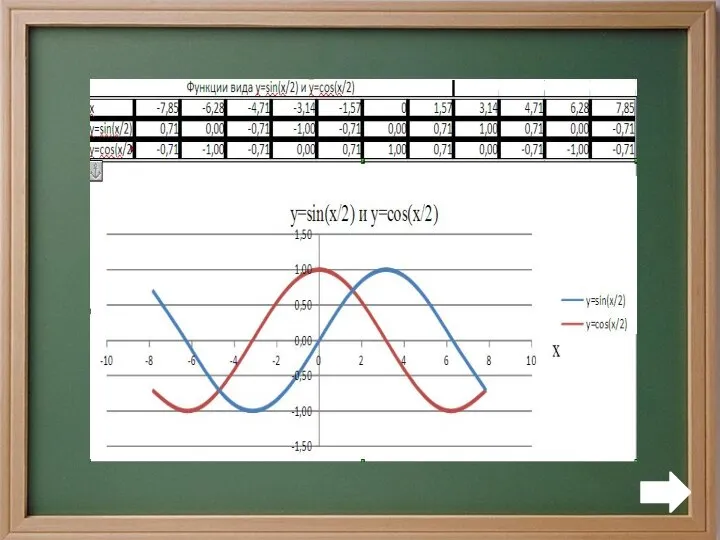
Построение графиков
Применение в других областях
Практикум

Слайд 4Историческая справка
Деятельность Эйлера многогранна и разностороння.
Он занимался почти всем, что интересовало в

то время
математиков.
С. И. Вавилов
Слайд 5Эйлер усовершенствовал как символику,
так и содержание тригонометрии. Вот его заслуги:
1.Он в первые

доступно изложил вопрос о знаках тригонометрических функций в каждом квадранте.
2.Эйлер исключил из своих формул R-целый синус, принимая R=1 и упрощая таким образом записи и вычисления.
3.Так же Эйлер впервые трактует синус, косинус как тригонометрические линии , обязательно связанные с окружностью , а как тригонометрические функции.
4.Эйлер впервые стал систематически излагать тригонометрию аналитическим путем.
5.Лишь в его трудах разрабатывается учение о тригонометрических функциях
любого аргумента.






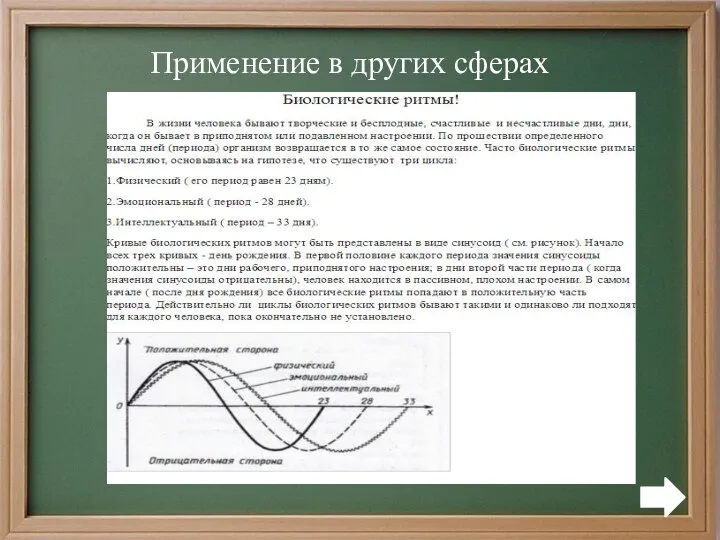


 Окружность и длина окружности
Окружность и длина окружности К уроку математики
К уроку математики Доли. Обыкновенные дроби. 5 класс
Доли. Обыкновенные дроби. 5 класс 1_2_opredeliteli (1)
1_2_opredeliteli (1) Пифагор и литература
Пифагор и литература Графы
Графы Окружность и круг. Повторение 7 класс
Окружность и круг. Повторение 7 класс Применение подобия к доказательству теорем и решению задач. Урок 40
Применение подобия к доказательству теорем и решению задач. Урок 40 Решение систем линейных неравенств
Решение систем линейных неравенств Аттестационная работа. Доли. Обыкновенные дроби. (5 класс)
Аттестационная работа. Доли. Обыкновенные дроби. (5 класс)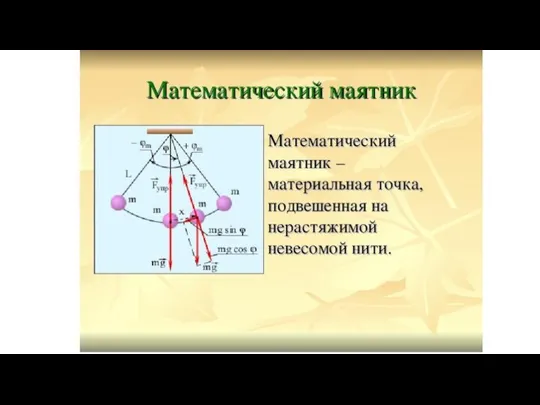 Математический маятник
Математический маятник Параллельные прямые 7 класс
Параллельные прямые 7 класс Применение векторов к решению задач. 9 класс
Применение векторов к решению задач. 9 класс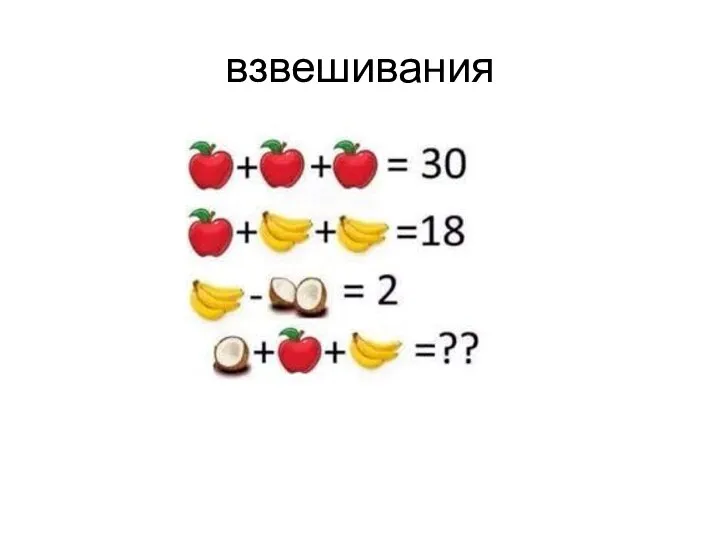 Взвешивания. Домашнее задание 1 класс
Взвешивания. Домашнее задание 1 класс Презентация на тему Обозначение натуральных чисел.Чтение и запись натуральных чисел
Презентация на тему Обозначение натуральных чисел.Чтение и запись натуральных чисел  Презентация по теории вероятностей. На тему:”Описательная статистика”.
Презентация по теории вероятностей. На тему:”Описательная статистика”. Понятия возрастающей и убывающей функций
Понятия возрастающей и убывающей функций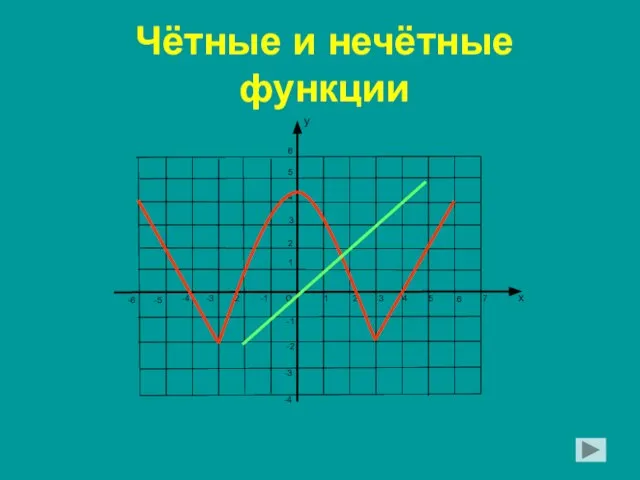 Презентация на тему Четные и нечетные функции
Презентация на тему Четные и нечетные функции  Разложение на множители разными способами
Разложение на множители разными способами Логарифмы. Задание
Логарифмы. Задание Комбинаторные задачи
Комбинаторные задачи Умножение и деление с числами 1,0. Деление нуля на число
Умножение и деление с числами 1,0. Деление нуля на число Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Решение задач на проценты (%)
Решение задач на проценты (%) Квадрат и куб числа
Квадрат и куб числа Математика вокруг нас
Математика вокруг нас Obratnye_trigonometricheskie_funktsii (1)
Obratnye_trigonometricheskie_funktsii (1) Значение переменных верного равенства. Корни уравнений
Значение переменных верного равенства. Корни уравнений