Скалярное произведение векторов

Повторяем теорию:
Как находят координаты вектора, если известны координаты его начала и конца?
Как находят координаты середины отрезка?
Как находят длину вектора?
Как находят расстояние между точками?
Как вы понимаете выражение «угол между векторами»?

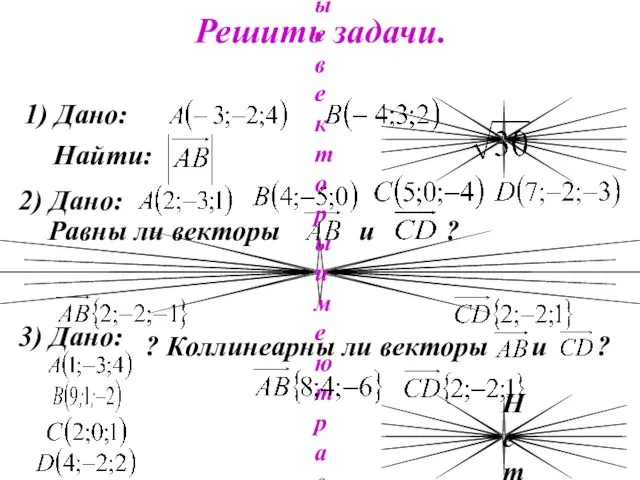
Решить задачи.
1) Дано:
Найти:
2) Дано:
Равны ли векторы и ?
Нет, т.к.равные векторы имеют равные
координаты.
3) Дано:
? Коллинеарны ли векторы и ?
Нет

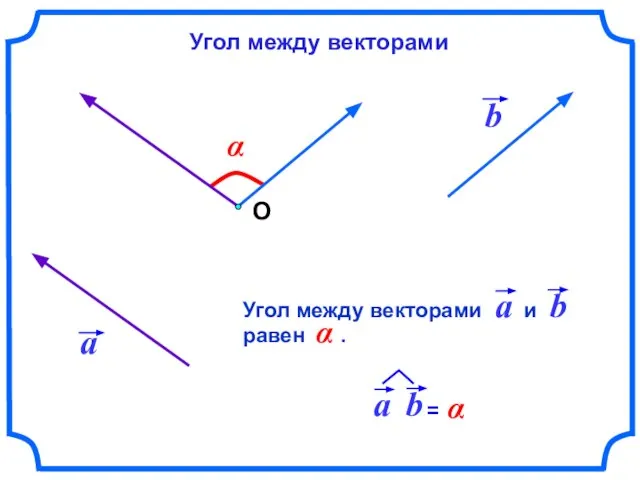
α
О
Угол между векторами

Угол между векторами.
О
А
В
α
Если то
Если то
Если то

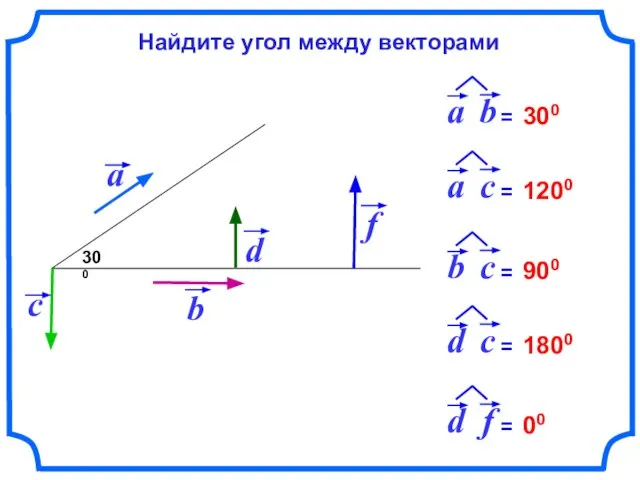
300
300
1200
900
1800
00
Найдите угол между векторами

Скалярное произведение векторов – число (скаляр).
Скалярным произведением двух векторов называется произведение
их длин на косинус угла между ними.
Определение

Если , то
Если
, то
Если
, то
Если
, то
Скалярное произведение
называется
скалярным квадратом вектора
Вспомним планиметрию…

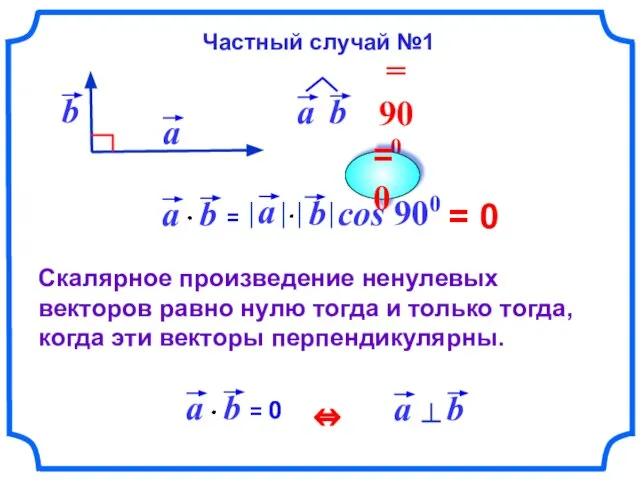
= 0
Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
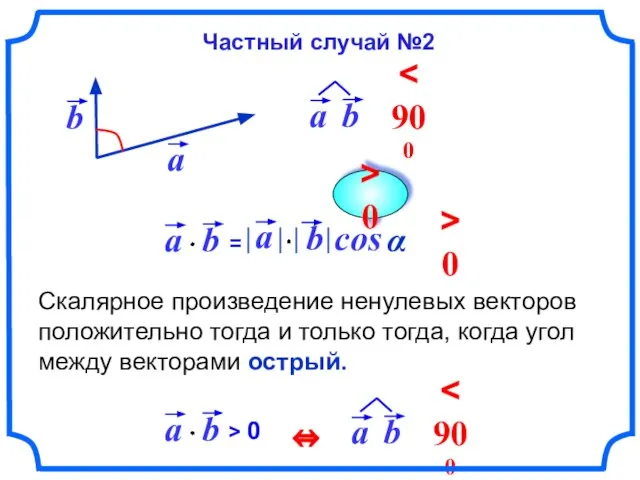
Частный случай №1
= 0

Скалярное произведение ненулевых векторов положительно тогда и только тогда, когда угол между векторами острый.
cos
α
> 0
> 0
Частный случай №2

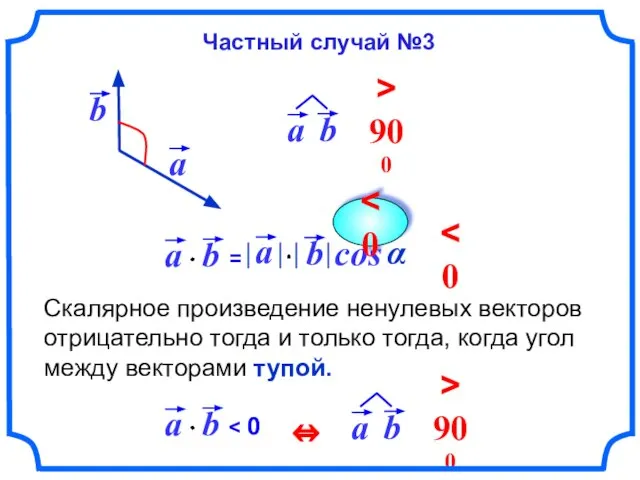
Скалярное произведение ненулевых векторов отрицательно тогда и только тогда, когда угол между векторами тупой.
cos
α
< 0
< 0
Частный случай №3

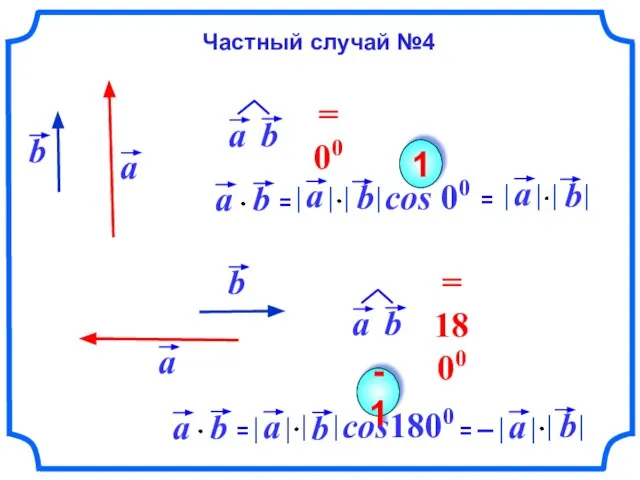
cos 00
1
cos1800
-1
Частный случай №4

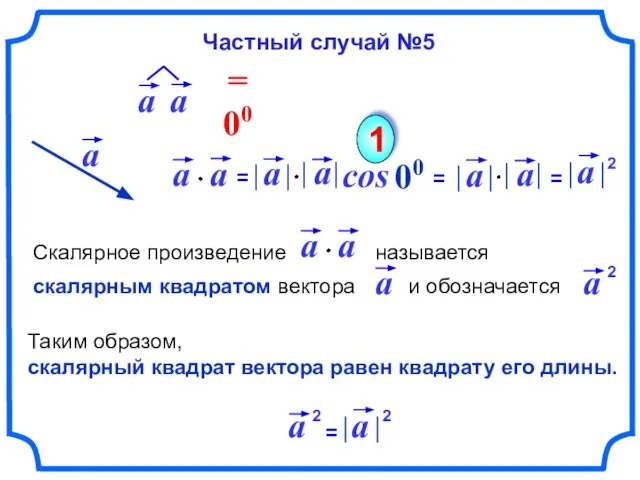
cos
00
1
Таким образом,
скалярный квадрат вектора равен квадрату его длины.
Частный случай №5
2
2
2
2

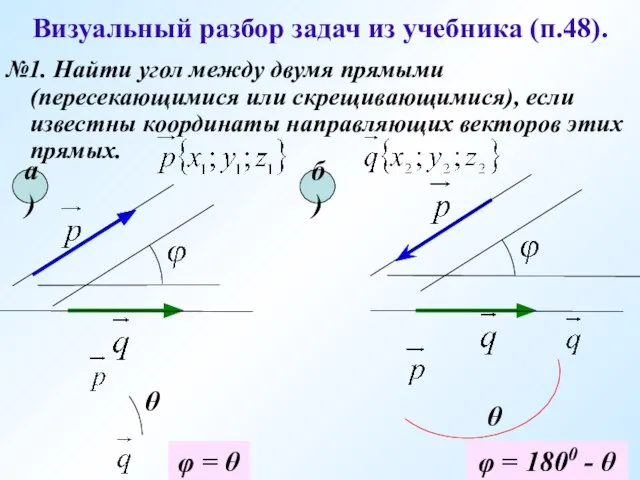
Визуальный разбор задач из учебника (п.48).
№1. Найти угол между двумя прямыми (пересекающимися или скрещивающимися), если известны координаты направляющих векторов этих прямых.
а)
б)
θ
θ
φ = θ
φ = 1800 - θ

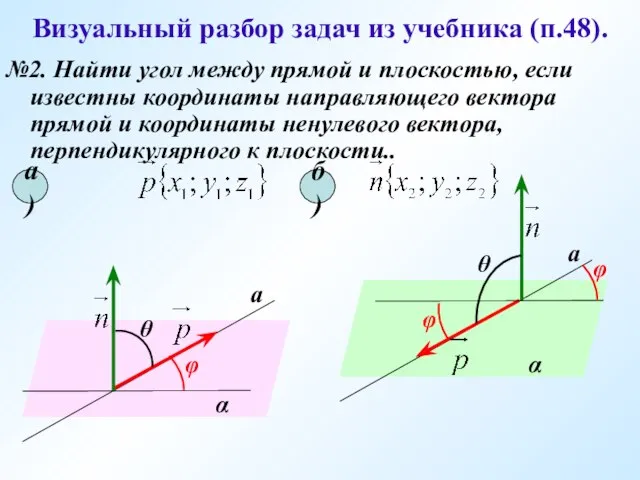
Визуальный разбор задач из учебника (п.48).
№2. Найти угол между прямой и плоскостью, если известны координаты направляющего вектора прямой и координаты ненулевого вектора, перпендикулярного к плоскости..
а)
б)
α
а
φ
θ
α
а
φ
φ
θ

Формула скалярного произведения векторов в пространстве.
Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.

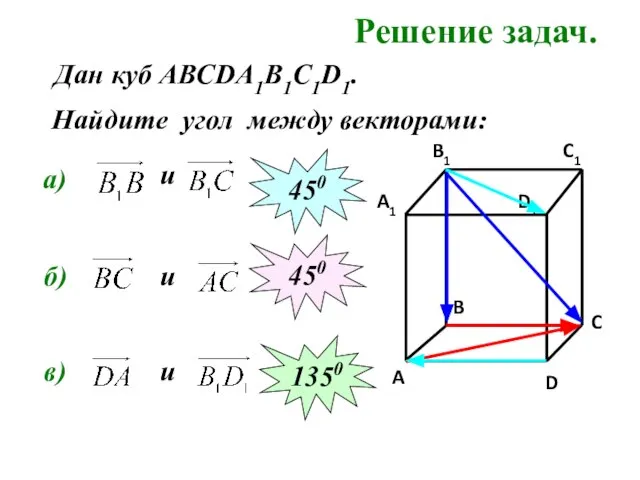
Решение задач.
Найдите угол между векторами:
а)
и
450
б)
и
450
в)
Дан куб АВСDA1B1C1D1.
и
1350

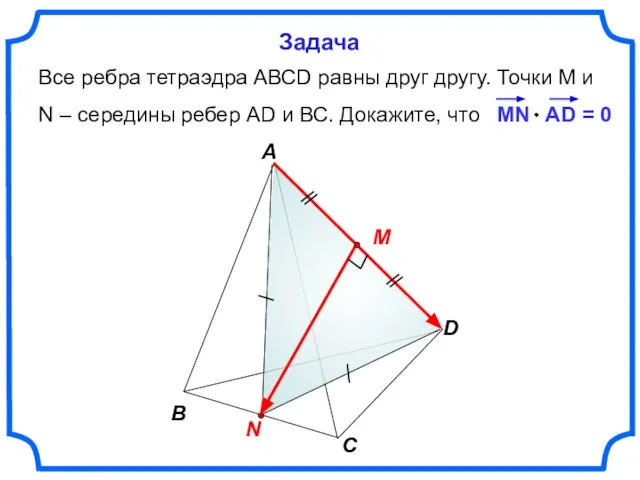
Все ребра тетраэдра АВСD равны друг другу. Точки М и
N – середины ребер АD и ВС. Докажите, что
B
C
N
A
D
M
Задача

Формула для нахождения скалярного произведения
через координаты векторов
= x1x2 + y1y2 + z1z2

Пример №1
Найти скалярное произведение векторов:
a {-6; 9; 5}
b {-1; 0; 7}

Пример №2
Найти скалярное произведение векторов:
a {0; 0; 4}
b {22; 1; 8}

Пример №3
Найти скалярное произведение векторов:
a {1; 7; 9}
b {-2; 4; 0}

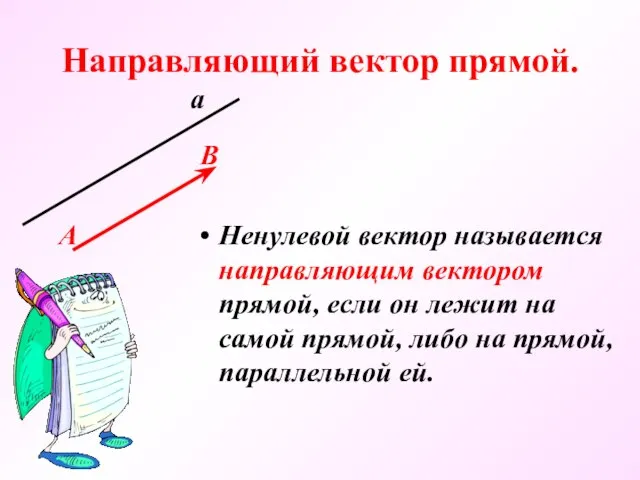
Направляющий вектор прямой.
Ненулевой вектор называется направляющим вектором прямой, если он лежит на самой прямой, либо на прямой, параллельной ей.
а
В
А

№ 464 (а)
Дано:
Найти: угол между прямыми АВ и CD.
Ваши предложения…
Найдем координаты векторов
и
2. Воспользуемся формулой:
φ = 300

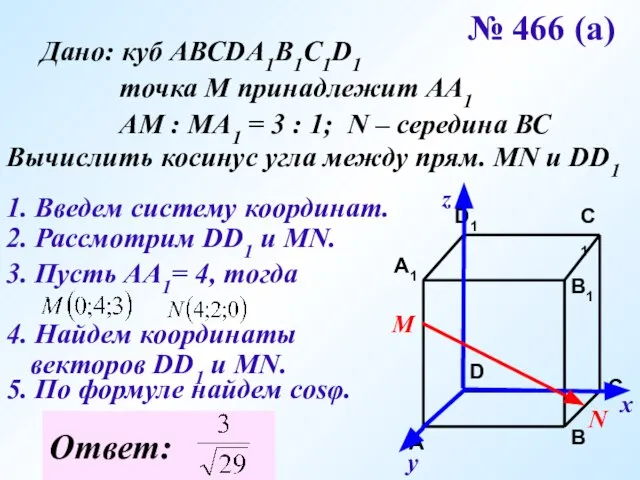
№ 466 (а)
Дано: куб АВСDA1B1C1D1
точка М принадлежит АА1
АМ : МА1 = 3 : 1; N – середина ВС
Вычислить косинус угла между прям. MN и DD1
1. Введем систему координат.
х
у
z
2. Рассмотрим DD1 и МN.
М
N
3. Пусть АА1= 4, тогда
4. Найдем координаты векторов DD1 и MN.
5. По формуле найдем cosφ.
Ответ:

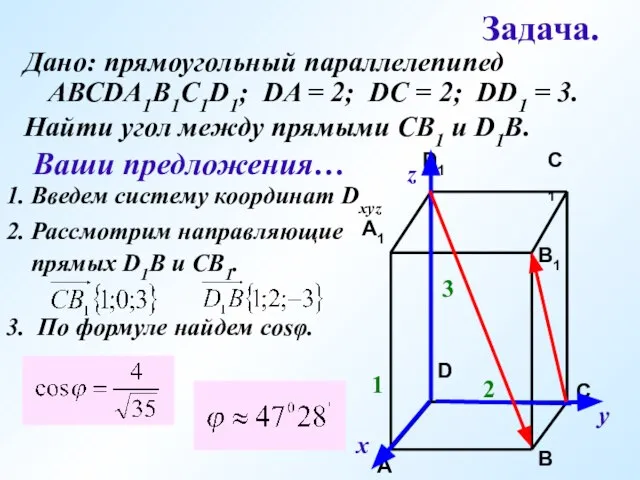
Задача.
Дано: прямоугольный параллелепипед АВСDA1B1C1D1; DA = 2; DC = 2; DD1 = 3.
1
2
3
Найти угол между прямыми СВ1 и D1B.
х
у
z
Ваши предложения…
1. Введем систему координат Dxyz
2. Рассмотрим направляющие
прямых D1B и CB1.
3. По формуле найдем cosφ.

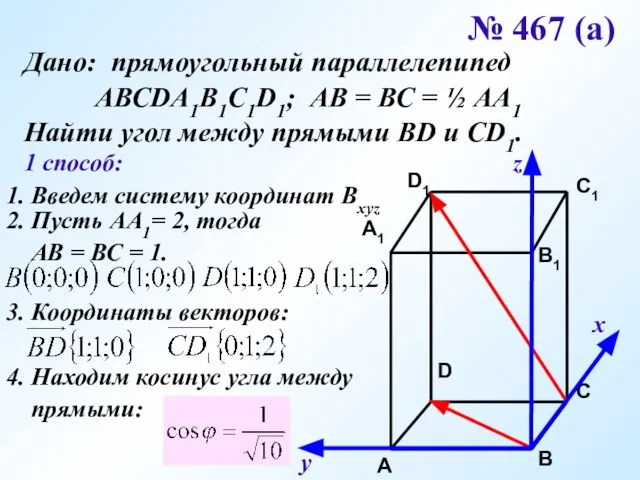
№ 467 (а)
Дано: прямоугольный параллелепипед
АВСDA1B1C1D1; АВ = ВС = ½ АА1
Найти угол между прямыми ВD и CD1.
1 способ:
1. Введем систему координат Bxyz
х
у
z
2. Пусть АА1= 2, тогда
АВ = ВС = 1.
3. Координаты векторов:
4. Находим косинус угла между
прямыми: