Взаимное расположение сферы и плоскости

“
Шар и сфера --это обычные геометрические понятия или нечто большее?

"Высшее назначение геометрии как раз состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает". Винер

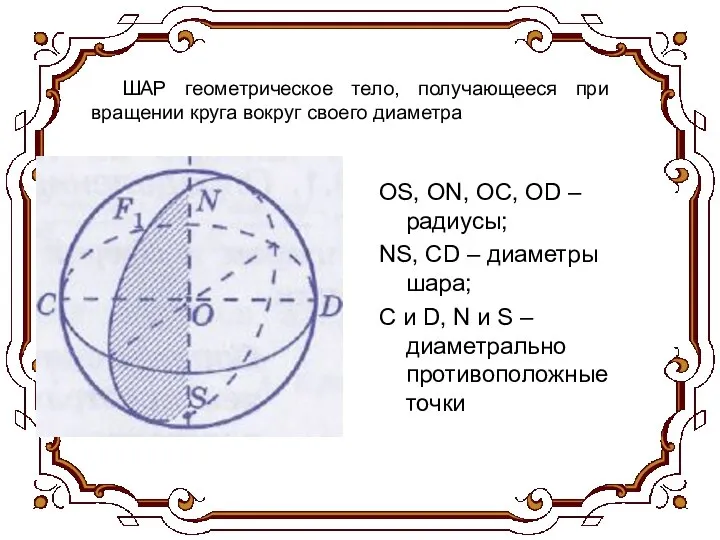
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
Эта точка называется центром шара.
А данное расстояние радиусом шара.
Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром.
Тело, ограниченное сферой, называется шаром.
Вспомним теорию

OS, ON, OC, OD – радиусы;
NS, CD – диаметры шара;
C и D, N и S – диаметрально противоположные точки
ШАР геометрическое тело, получающееся при вращении круга вокруг своего диаметра

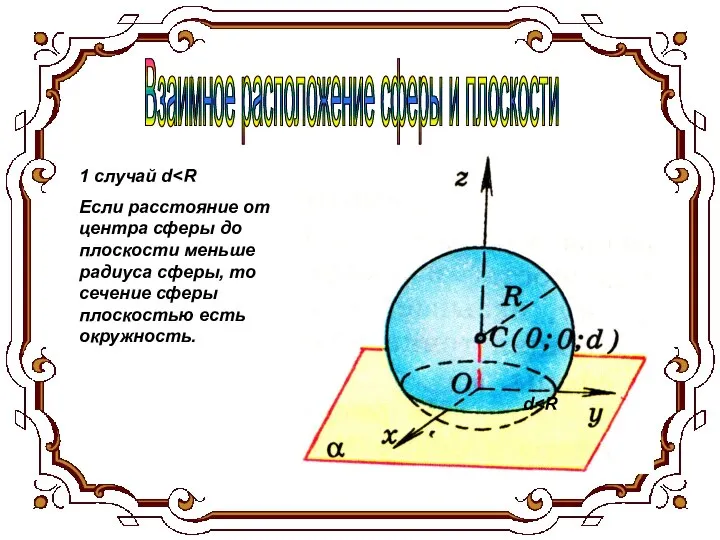
Взаимное расположение сферы и плоскости
1 случай d
Если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность.
d

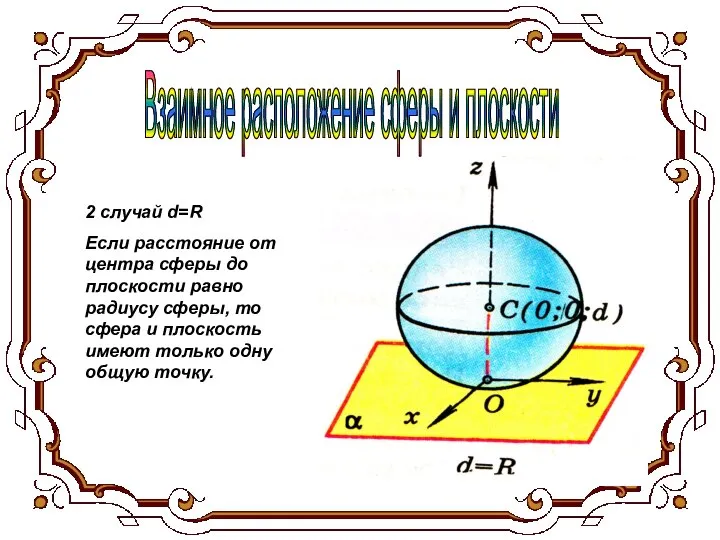
Взаимное расположение сферы и плоскости
2 случай d=R
Если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку.

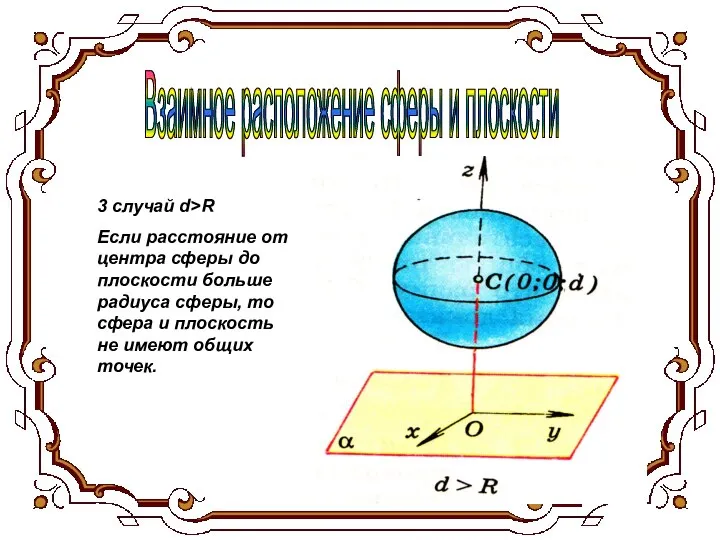
Взаимное расположение сферы и плоскости
3 случай d>R
Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

За площадь сферы примем предел последовательности площадей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани
объем шара определяется по формуле вычисления объема тел вращения:
Объем шара равен:
площадь сферы объём шара

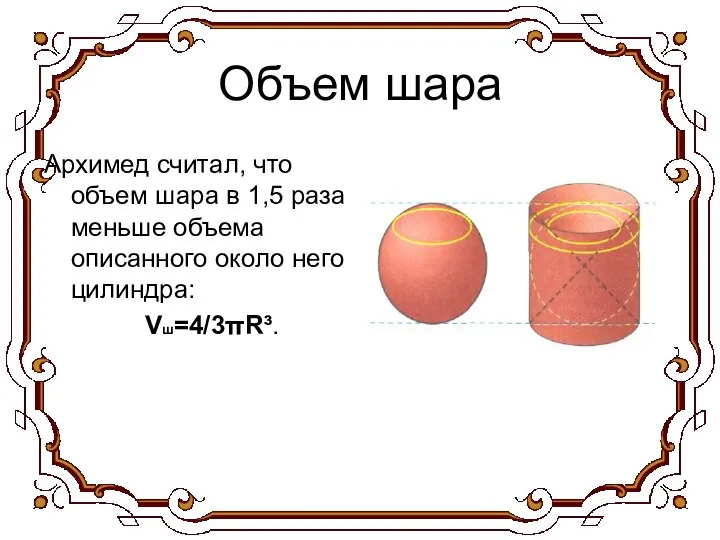
Объем шара
Архимед считал, что объем шара в 1,5 раза меньше объема описанного около него цилиндра:
Vш=4/3πR³.

ЗАДАЧА
Земной шар стянут обручем по экватору, и точно так же «по экватору» стянут обручем апельсин. Представим, что длина каждого обруча увеличилась на 1 м. При этом между поверхностями этих тел и их обручами образуется зазор.
В каком случае этот зазор будет больше — у земного шара или апельсина?
Решим задачу

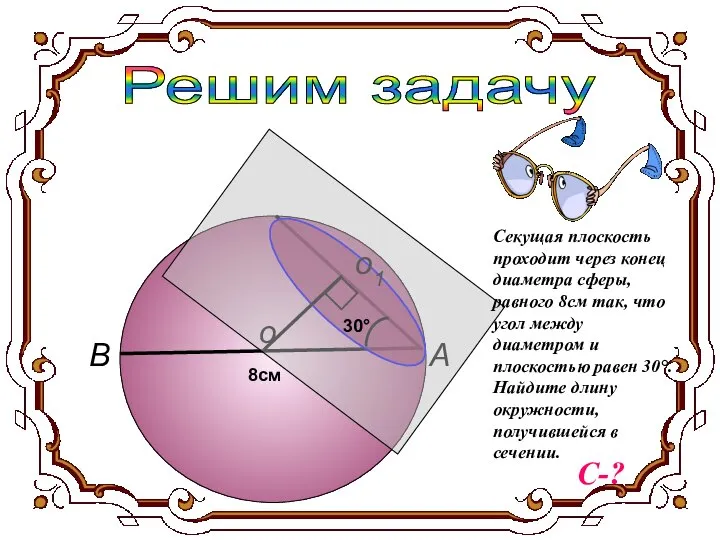
Решим задачу
о1
А
В
о
8см
30°
Секущая плоскость проходит через конец диаметра сферы, равного 8см так, что угол между диаметром и плоскостью равен 30°. Найдите длину окружности, получившейся в сечении.
С-?

Решим задачу