Содержание
- 2. Производная
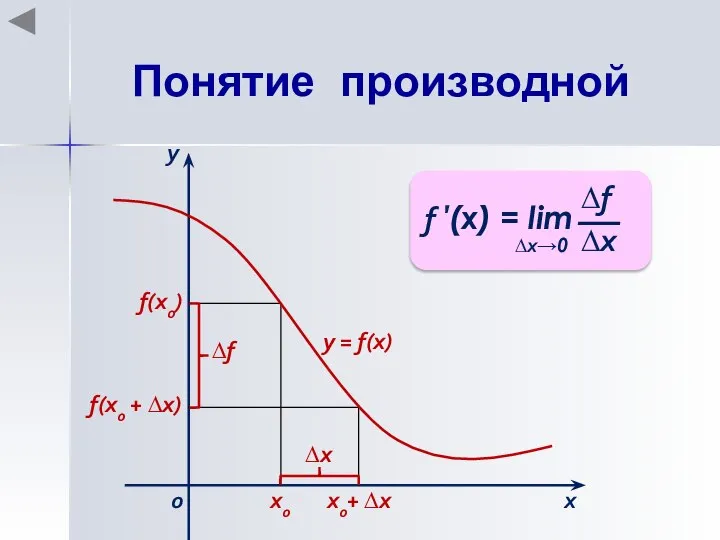
- 3. Понятие производной Производной функции у = f(x), заданной на некотором интервале (a; b), в некоторой точке
- 4. Понятие производной х0 х0+ ∆х f(x0) f(x0 + ∆х) ∆х х у 0 ∆f у =
- 5. Зафиксировать значение х0, найти f(x0). Дать аргументу х0 приращение ∆х, перейти в новую точку х0 +
- 6. Примеры 1. Найти производную функции y = kx + b в точке хo
- 7. Примеры 2. Найти производную функции y = C (C – const) в точке хo
- 8. Примеры 3. Найти производную функции y = x2 в точке хo
- 9. Примеры
- 10. Примеры
- 11. Примеры 5. Найти производную функции y = 1/x в точке хo
- 12. Примеры 5. Найти производную функции y = 1/x в точке хo
- 13. Правила нахождения производной 1. Если функции u(x) и v(x) имеют в точке х производные, то их
- 14. Правила нахождения производной 3. Если функции u(x) и v(x) имеют в точке х производные, то их
- 15. Правила нахождения производной 5. Если функции u(x) и v(x) имеют в точке х производные и v(x)
- 16. Если функция имеет производную (дифференцируема) в точке х, то она непрерывна в этой точке.
- 17. ТАБЛИЦА ПРОИЗВОДНЫХ
- 18. ТАБЛИЦА ПРОИЗВОДНЫХ ПРАВИЛА ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ
- 19. №1. Найдите производные функций:
- 31. Скачать презентацию

















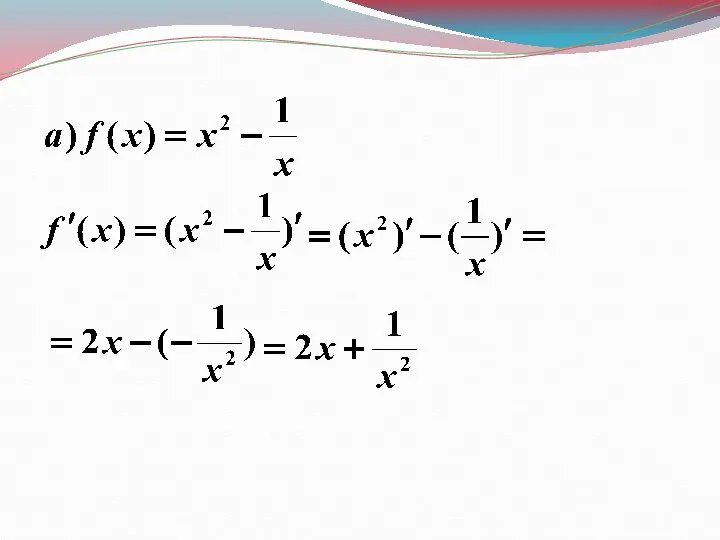
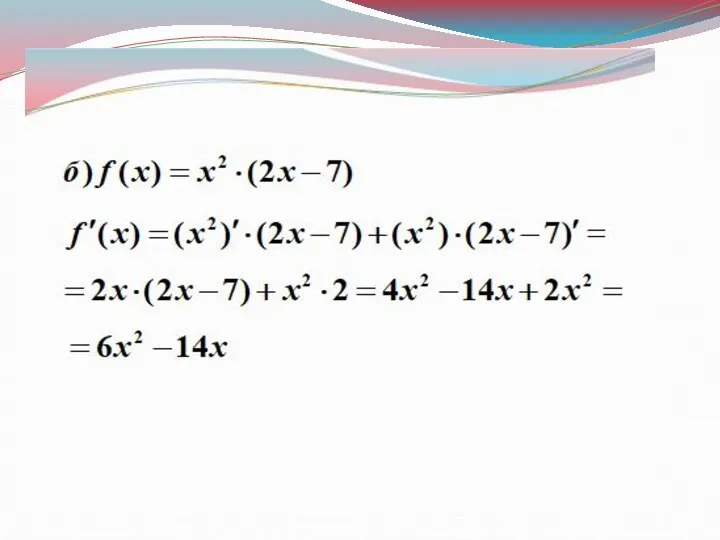
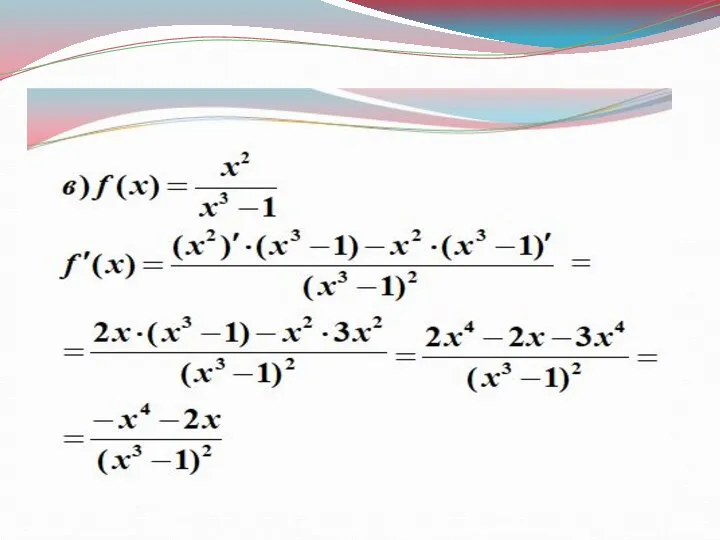
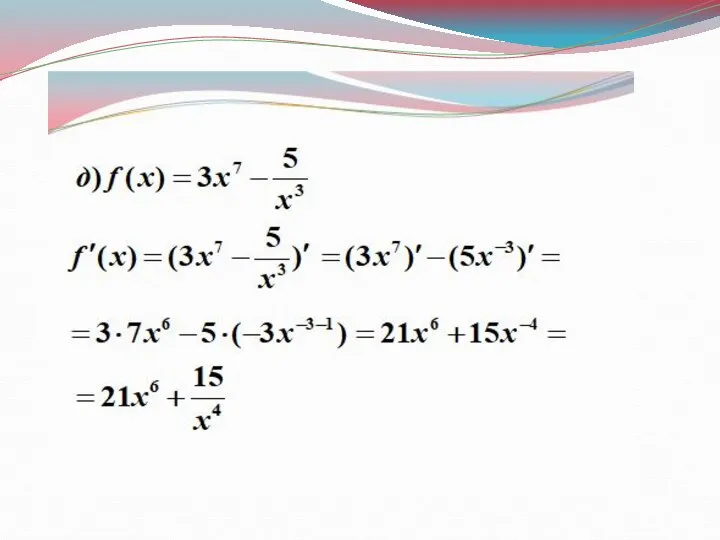

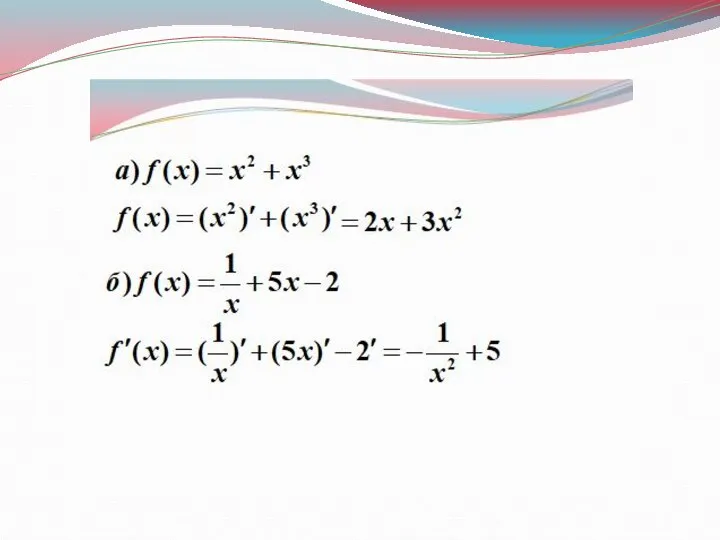
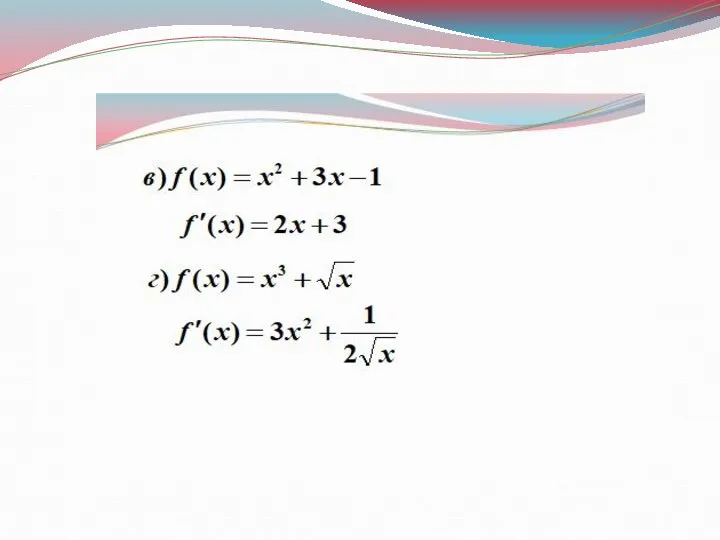

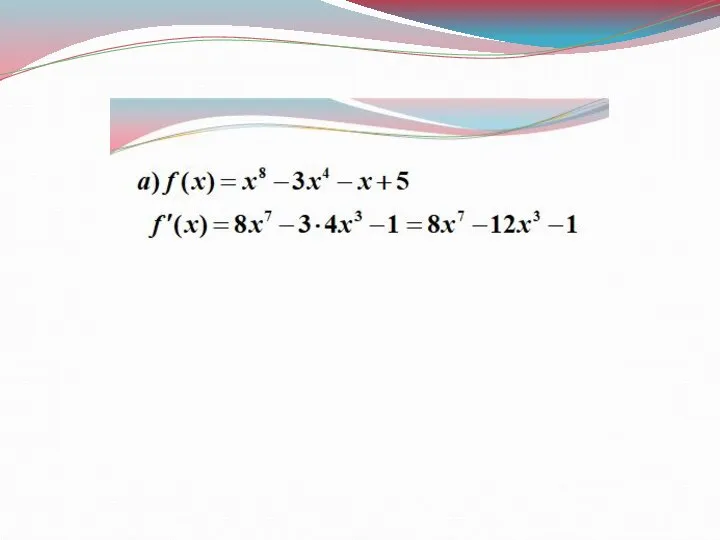
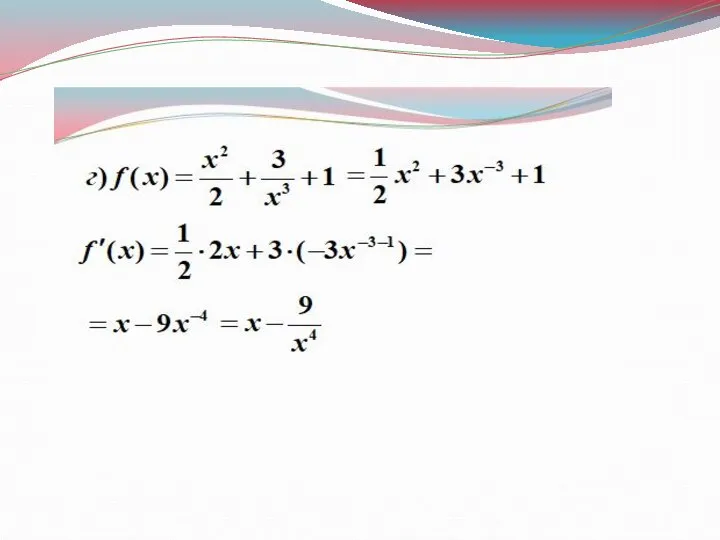
 Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс Величины. Длина
Величины. Длина Случайные величины 14 сен
Случайные величины 14 сен Возникновение первых математических понятий
Возникновение первых математических понятий Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс
Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс Умножение на 1 и 0
Умножение на 1 и 0 Диктант по геометрии
Диктант по геометрии Выбор схемы измерения переменных
Выбор схемы измерения переменных Умножение на 10,100,1000, 0,1, 0,01, 0,001
Умножение на 10,100,1000, 0,1, 0,01, 0,001 Подготовка к блиц-турниру
Подготовка к блиц-турниру Скалярное прозведение векторов
Скалярное прозведение векторов Шифр Цезаря
Шифр Цезаря Сфера и шар
Сфера и шар Многогранники. Призма
Многогранники. Призма Пропорции и проценты
Пропорции и проценты Координаты суммы, разности и произведения вектора на число
Координаты суммы, разности и произведения вектора на число Графический диктант
Графический диктант Презентация на тему Расположение точек относительно осей координат
Презентация на тему Расположение точек относительно осей координат  Найдите высоту и медиану треугольника
Найдите высоту и медиану треугольника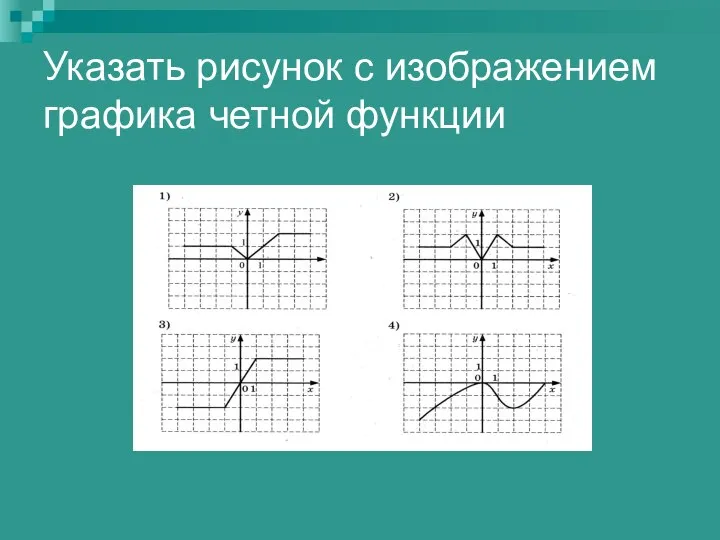 Указать рисунок с изображением графика четной функции
Указать рисунок с изображением графика четной функции Параллелепипед
Параллелепипед Выражение отношения в процентах
Выражение отношения в процентах Задачи на проценты. Схемы
Задачи на проценты. Схемы Решение нелинейных уравнений
Решение нелинейных уравнений Сложение с переходом через десяток. Тренажёр
Сложение с переходом через десяток. Тренажёр Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс
Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения
Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика