Содержание
- 2. Транспортная задача
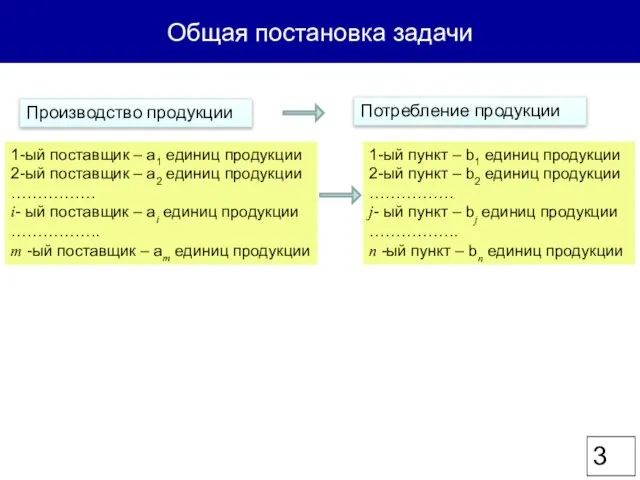
- 3. Общая постановка задачи Производство продукции Потребление продукции 1-ый поставщик – a1 единиц продукции 2-ый поставщик –
- 4. Общая постановка задачи Матрица транспортных расходов сi,j – стоимость перевозки из i-го пункта производства в j-й
- 5. Ограничения План называется допустимым, если хij, i = 1,…,т, j = 1,…,п удовлетворяют следующим естественным условиям:
- 6. Сведение к задаче линейного программирования Транспортная задача состоит в отыскании среди допустимых планов перевозок оптимального, то
- 7. Сведение к задаче линейного программирования Транспортная задача является задачей линейного программирования и может быть решена симплекс-методом,
- 8. Задание В предыдущих обозначениях:
- 9. Заполняем таблицу с исходными данными в соответствии с вариантом Объем потребления Объем производства Матрица транспортных расходов
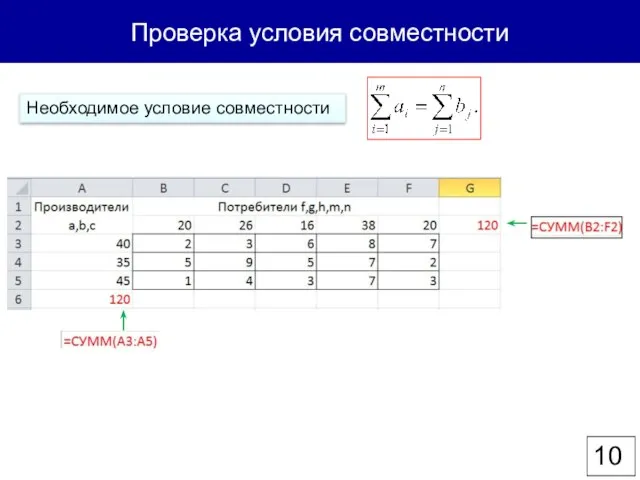
- 10. Проверка условия совместности Необходимое условие совместности
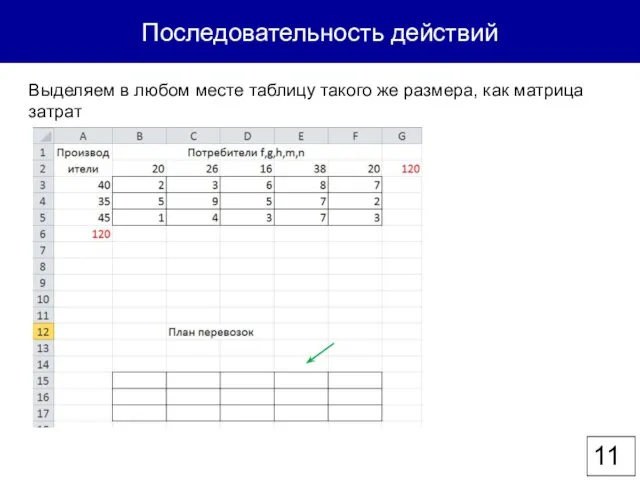
- 11. Последовательность действий Выделяем в любом месте таблицу такого же размера, как матрица затрат
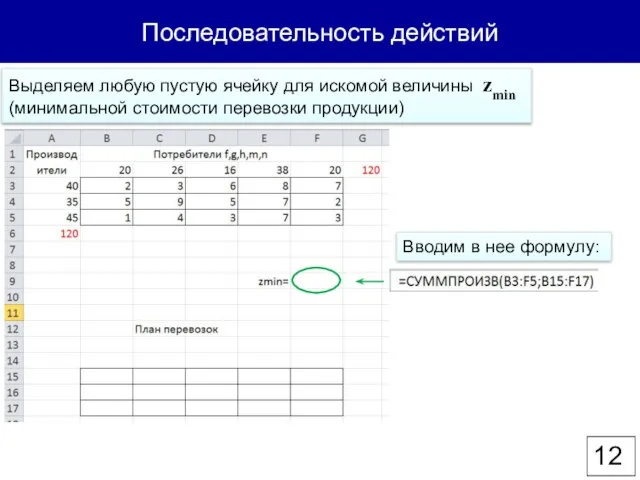
- 12. Последовательность действий Выделяем любую пустую ячейку для искомой величины zmin (минимальной стоимости перевозки продукции) Вводим в
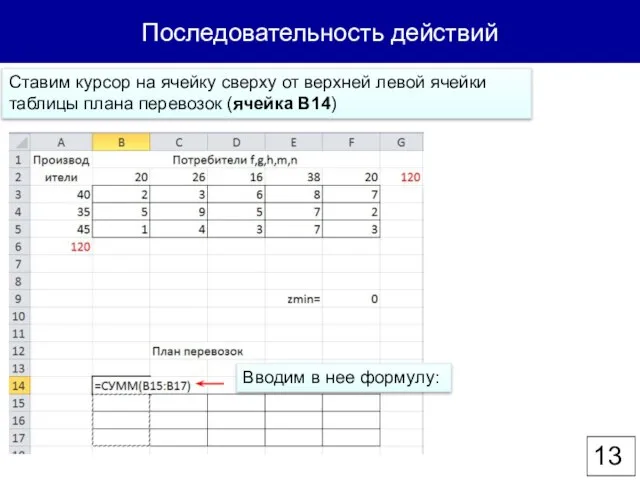
- 13. Последовательность действий Ставим курсор на ячейку сверху от верхней левой ячейки таблицы плана перевозок (ячейка В14)
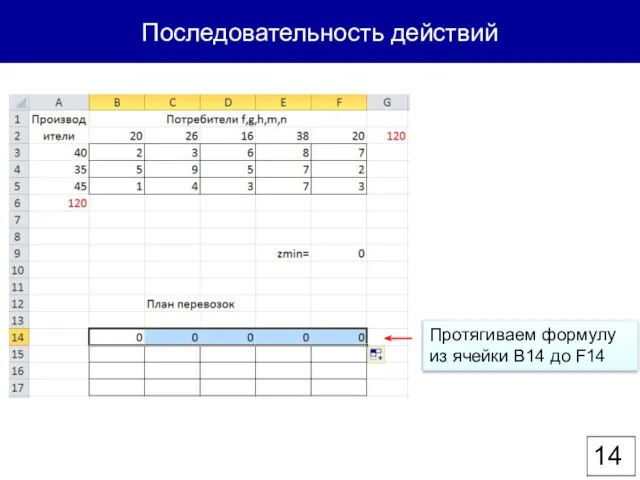
- 14. Последовательность действий Протягиваем формулу из ячейки B14 до F14
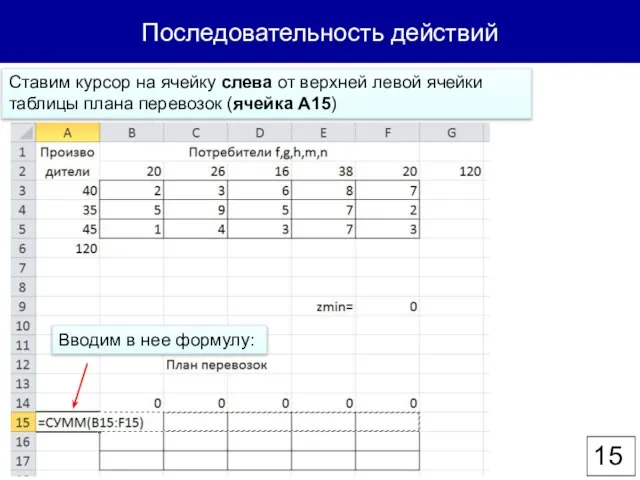
- 15. Последовательность действий Ставим курсор на ячейку слева от верхней левой ячейки таблицы плана перевозок (ячейка А15)
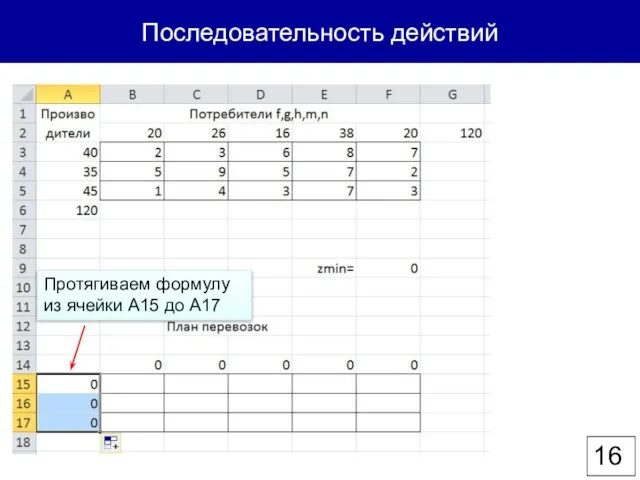
- 16. Последовательность действий Протягиваем формулу из ячейки А15 до А17
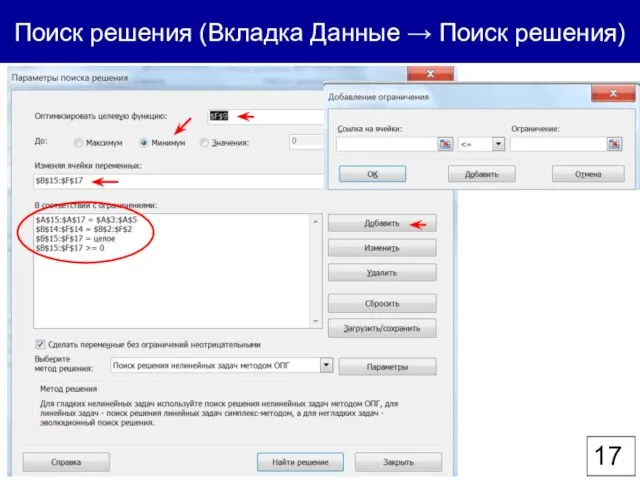
- 17. Поиск решения (Вкладка Данные → Поиск решения)
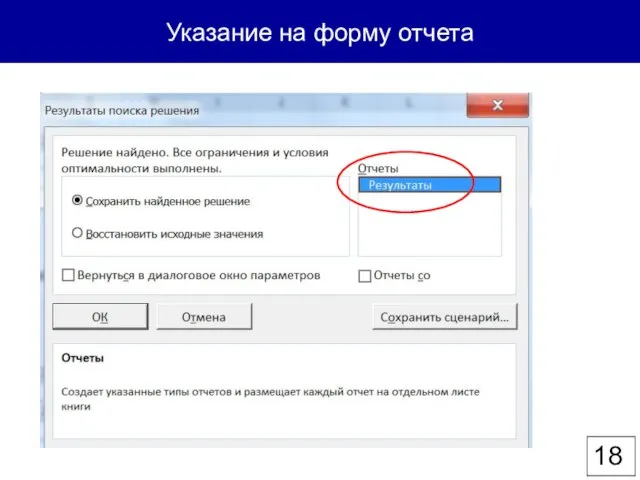
- 18. Указание на форму отчета
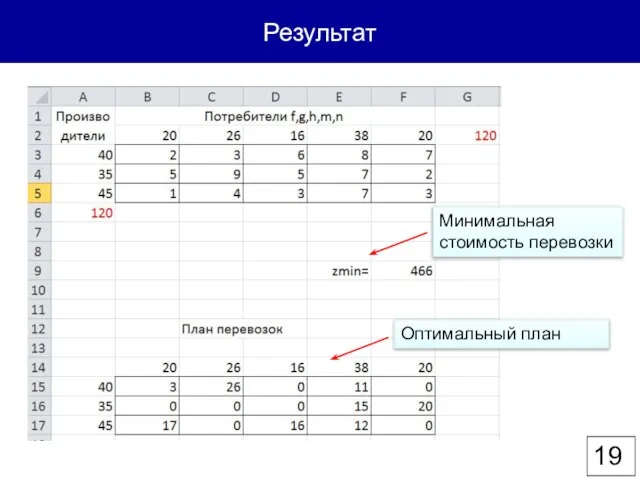
- 19. Результат Оптимальный план Минимальная стоимость перевозки
- 21. Скачать презентацию







 Подготовка к ГИА. Демоверсия 2013
Подготовка к ГИА. Демоверсия 2013 Мотивация … Статистика
Мотивация … Статистика Парная регрессия и корреляция
Парная регрессия и корреляция Простые и составные числа
Простые и составные числа Единицы измерения времени. Тренажёр
Единицы измерения времени. Тренажёр Дифференциальные уравнения
Дифференциальные уравнения Функция y=k/x, её график и свойства. 8 класс. Урок 2
Функция y=k/x, её график и свойства. 8 класс. Урок 2 Духовно-нравственное воспитание на уроках математики
Духовно-нравственное воспитание на уроках математики Особенности применения средств измерений в качестве эталонов единицы величины
Особенности применения средств измерений в качестве эталонов единицы величины Показательная функция
Показательная функция Теория расписаний. Минимизация приоритето-порождающих функций
Теория расписаний. Минимизация приоритето-порождающих функций Площадь треугольника
Площадь треугольника Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Коррекция СУ
Коррекция СУ Римские цифры. 3 класс
Римские цифры. 3 класс Нулевая гипотеза
Нулевая гипотеза Стандартный вид числа в физике, астрономии и технике
Стандартный вид числа в физике, астрономии и технике Презентация на тему Математический диктант (4 класс)
Презентация на тему Математический диктант (4 класс)  Свойства четырёхугольников
Свойства четырёхугольников idkwhythatair
idkwhythatair Виды многоугольников
Виды многоугольников Числа от 1 до 5. Состав числа 5
Числа от 1 до 5. Состав числа 5 Письмо цифры 6
Письмо цифры 6 Сложение смешанных дробей
Сложение смешанных дробей Среднее арифметическое
Среднее арифметическое Стереометрия. Подготовка к ЕГЭ, задание В11
Стереометрия. Подготовка к ЕГЭ, задание В11 Математические методы в экономике. Лекция 8
Математические методы в экономике. Лекция 8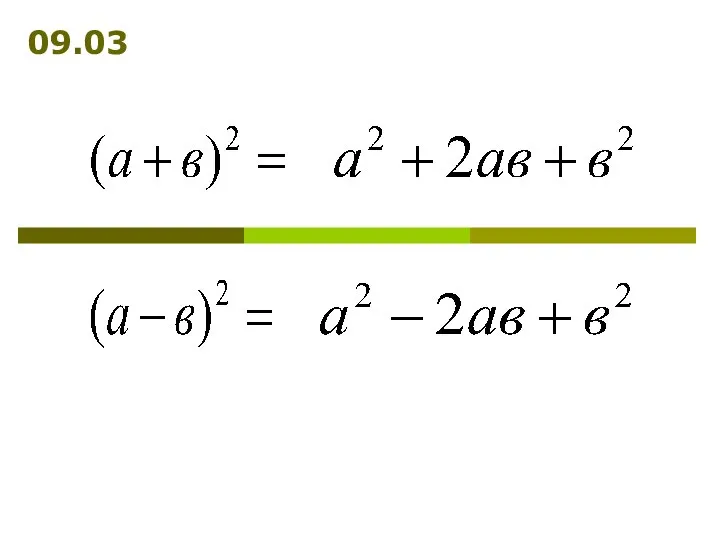 Преобразование многочленов с помощью формул сокращённого умножения
Преобразование многочленов с помощью формул сокращённого умножения