Алгоритмы решения простейших тригонометрических неравенств

Цель
Изучение алгоритмов решения простых тригонометрических неравенств
Задачи
изучить тригонометрические неравенства;
рассмотреть различные способы решения простых тригонометрических неравенств;
составить наиболее простой алгоритм решения тригонометрических неравенств;
научиться решать простые
тригонометрические неравенства.

Неравенство - это соотношение между двумя выражениями, указывающее, какое из них больше и какое меньше, посредством одного из знаков: < (меньше); > (больше); ≥ (больше или равно), < (меньше или равно).
Решить неравенство — это значит найти множество всех его решений.
Решением неравенства называются все значения переменной, при которых неравенство становится верным.

Тригонометрическое неравенство - неравенство, в котором неизвестная переменная находится под знаком тригонометрической функции.
Простое тригонометрическое неравенство – неравенство, в котором неизвестная переменная находится под знаком одной тригонометрической функции.

Способы решения тригонометрических неравенств
Решение тригонометрических неравенств с помощью числовой окружности;
Решение тригонометрических неравенств с помощью графика функции.

Решение тригонометрических неравенств с помощью числовой окружности
решение тригонометрических неравенств с синусом и косинусом;
решение тригонометрических неравенств с тангенсом и котангенсом.

Алгоритм решения тригонометрических неравенств
с синусом и косинусом
Перенести все числа в правую часть неравенства;
Начертить единичную окружность и отметить на ней ось sin или ось cos;
Отметить на оси число из правой части неравенства;
Через отмеченную точку провести прямую параллельную оси X или У;

Отметить точки пересечения прямой с окружностью, определить их значения;
Закрасить ту часть круга, которая является решением неравенства;
В закрашенной части указать стрелкой направление обхода окружности (против часовой стрелки);
Проверить, чтобы стрелка была направлена от меньшего угла к большему (если это не выполняется, то больший угол заменить соответствующим меньшим);
Записать ответ с учетом периода 2Пn.

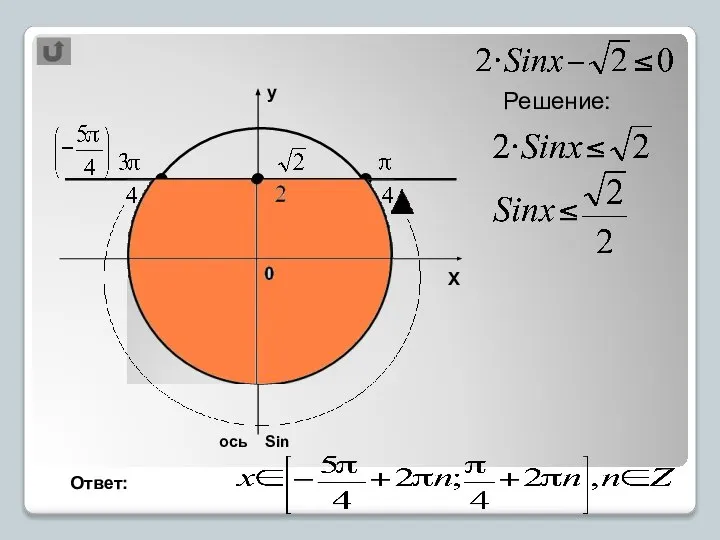
0
ось Sin
у
Х
Ответ:
Решение:

Алгоритм решения тригонометрических неравенств с тангенсом и котангенсом
1. Перенести все числа в правую часть неравенства;
2. Начертить единичную окружность и отметить на ней ось tg или ctg;
3. Отметить на оси число из правой части неравенства;
4. Через отмеченное число и центр окружности провести прямую;

5. Отметить точки пересечения прямой с окружностью, определить их значение;
6. Отметить на окружности точки в которых tg и ctg не пределен;
7. Закрасить ту часть круга, которая является решением неравенства;
8. В закрашенной части указать направление обхода окружности (против часовой стрелки);
9. Проверить, чтобы стрелка была направлена от меньшего угла к большему (если это не выполняется, то больший угол заменить соответствующим меньшим);
10. Записать ответ с учетом периода Пn.

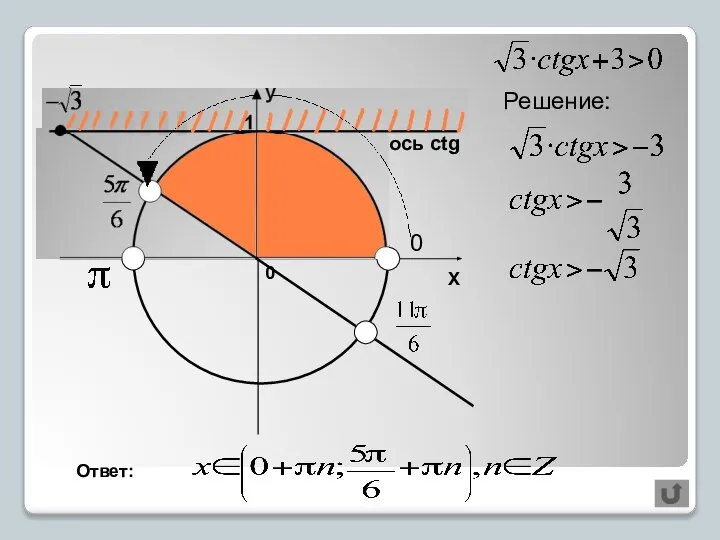
0
ось сtg
у
Х
Ответ:
Решение:
0

Алгоритм решения тригонометрических неравенств с помощью графика функции
Перенести все числа в правую часть неравенства;
Выписать функции входящие в неравенство;
Построить в одной системе координат графики этих функций;
Отметить на рисунке точки пересечения графиков функций;
Выделить части графиков, удовлетворяющие неравенству;
Записать ответ, учитывая период тригонометрической функции входящей в неравенство.

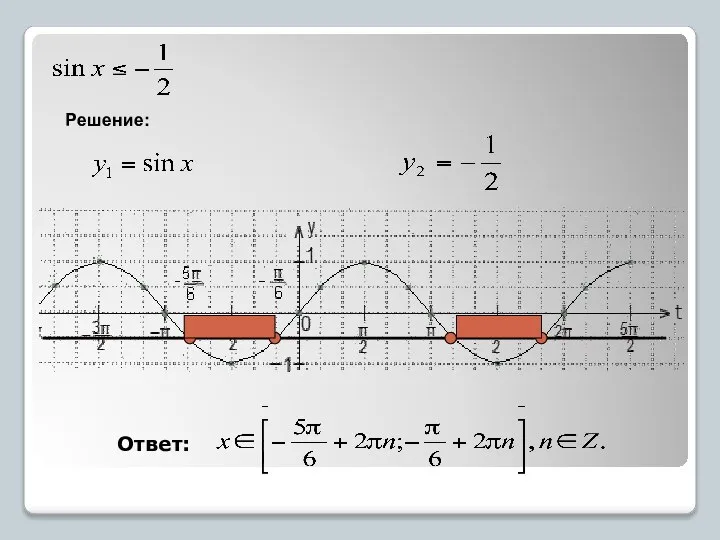
Решение:
Ответ: