Содержание
- 2. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
- 3. (выберете правильный ответ) Чем является предложение «Дети любят игрушки» с точки зрения алгебры логики? Неправильно Неправильно
- 4. (выберете правильный ответ) 2. Инверсия – это? Правильно Неправильно Неправильно Неправильно Логическое отрицание Логическая переменная Логическое
- 5. (выберете правильный ответ) 3. Логическое сложение – это? Неправильно Неправильно Неправильно Правильно Инверсия Импликация Конъюнкция Дизъюнкция
- 6. (выберете правильный ответ) 4. Логическое умножение? Правильно Неправильно Неправильно Неправильно Конъюнкция Эквивалентность Импликация Дизъюнкция
- 7. (выберете правильный ответ) 5. Логическое следование (Импликация) обозначается словами или знаком? Неправильно Правильно Неправильно Неправильно Или
- 8. (выберете правильный ответ) 6. Операция обозначенная словами В ТОГДА И ТОЛЬКО ТОГДА, КОГДА А называется? Неправильно
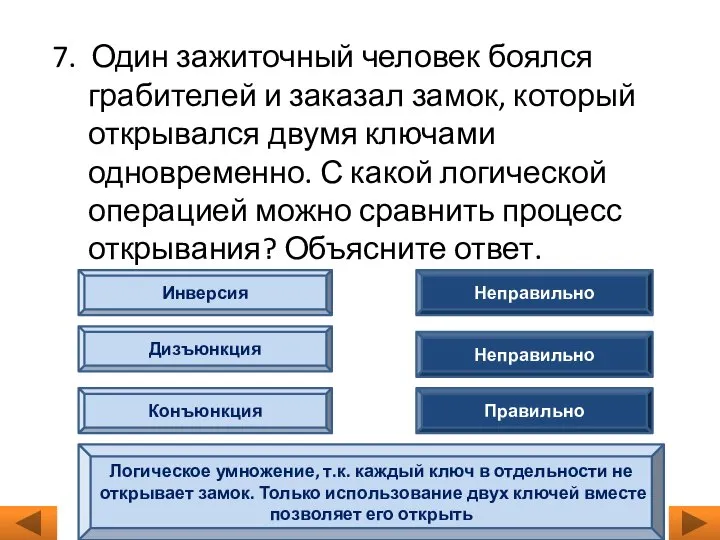
- 9. 7. Один зажиточный человек боялся грабителей и заказал замок, который открывался двумя ключами одновременно. С какой
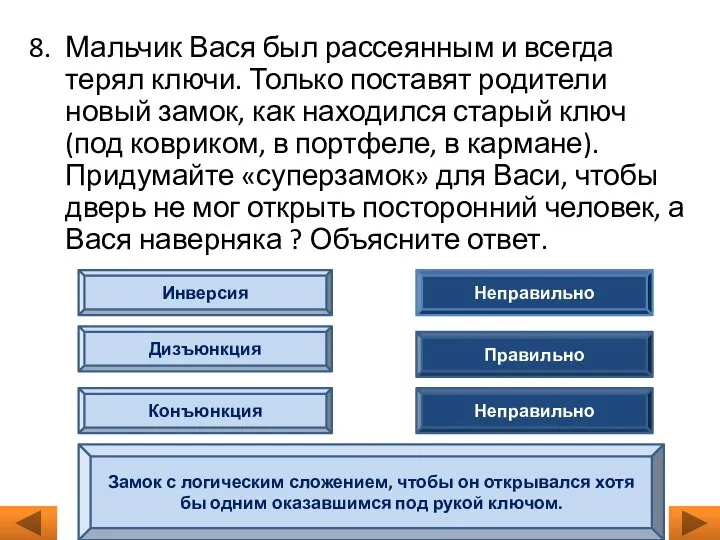
- 10. 8. Мальчик Вася был рассеянным и всегда терял ключи. Только поставят родители новый замок, как находился
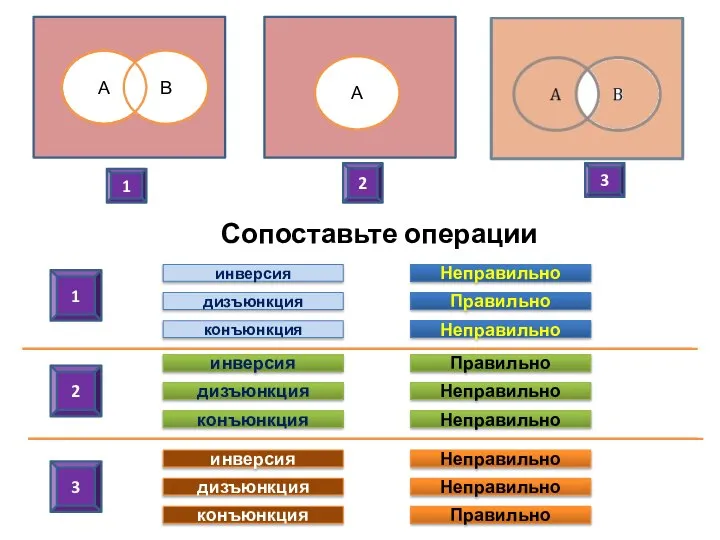
- 11. Сопоставьте операции 1 1 2 3 инверсия дизъюнкция конъюнкция инверсия дизъюнкция конъюнкция инверсия дизъюнкция конъюнкция Неправильно
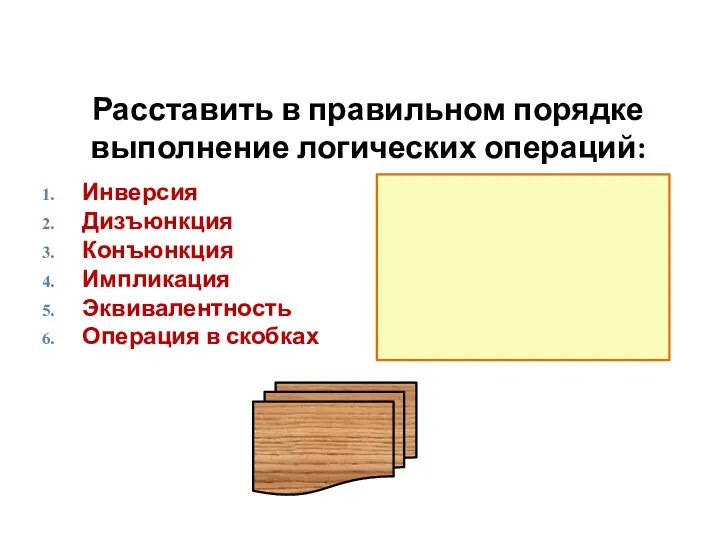
- 12. Расставить в правильном порядке выполнение логических операций: Инверсия Дизъюнкция Конъюнкция Импликация Эквивалентность Операция в скобках Операция
- 13. Основные законы Действия с абсолютно-истинными и абсолютно-ложными высказываниями Коммутативность Ассоциативность Дистрибутивность Идемпотентность Инволюция Поглощение Поглощение отрицания
- 14. Коммутативность (независимость от перестановки мест)
- 15. Ассоциативность (независимость от порядка выполнения однотипных действий)
- 16. Дистрибутивность (распределительный закон) Относительно логического умножения Относительно логического сложения
- 17. Идемпотентность (отсутствие степеней и коэффициентов)
- 18. Инволюция (двойное отрицание)
- 19. Действия с абсолютно-истинными и абсолютно-ложными высказываниями Закон исключенного третьего Закон противоречия
- 20. Законы де Моргана Отрицание одновременной истинности Отрицание вариантов
- 21. Поглощение
- 22. Поглощение отрицания
- 23. Закон исключения (склеивания) (AΛB)V(¬АΛB) =B (AVB)Λ(¬АVB)=B
- 24. Закон контрапозиции ¬(А→В) = АΛ¬В ¬(А→В)=¬А∙¬В А→В= ¬А+В
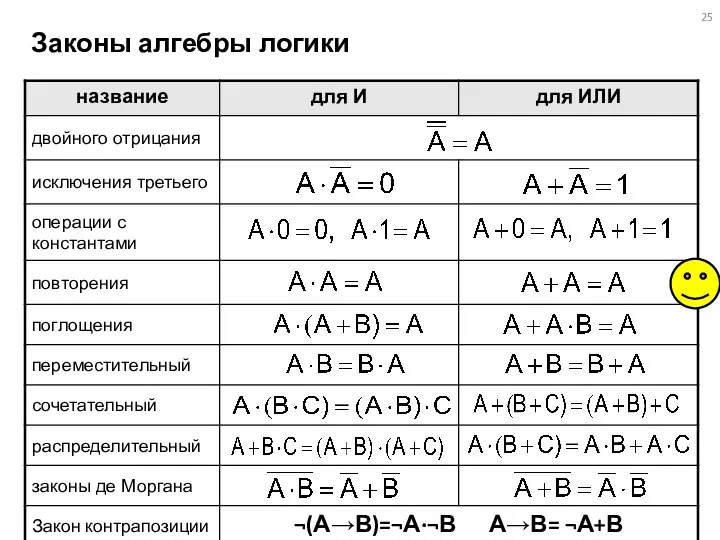
- 25. Законы алгебры логики
- 26. Упрощение логических выражений Шаг 1. Заменить операции →↔ на их выражения через И, ИЛИ и НЕ:
- 27. Упрощение логических выражений раскрыли → формула де Моргана распределительный исключения третьего повторения поглощения
- 28. Задачи (упрощение): _ X ∙ Y V X ∙ Y Воспользуемся распределительным законом: A ∙ (
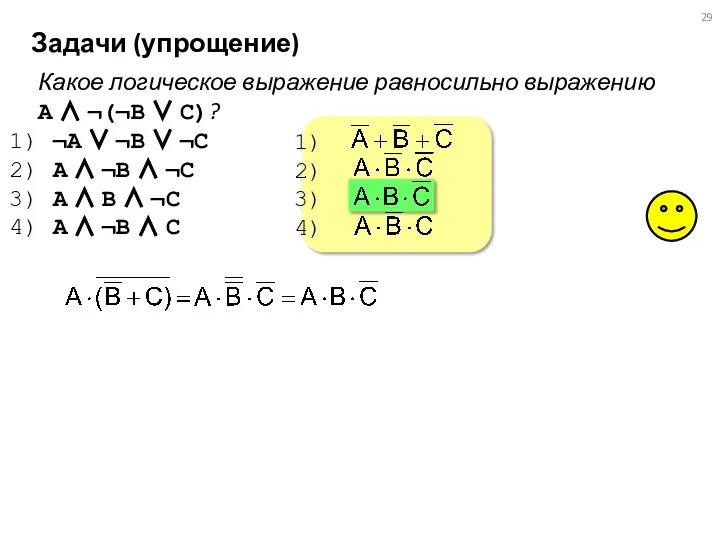
- 29. Задачи (упрощение) Какое логическое выражение равносильно выражению A ∧ ¬(¬B ∨ C)? ¬A ∨ ¬B ∨
- 31. Скачать презентацию



















 Комбинаторная задача с монетами
Комбинаторная задача с монетами Тестовые задания
Тестовые задания Производная и ее применение
Производная и ее применение Окружность и круг
Окружность и круг Математическая статистика
Математическая статистика Методы расчета ферм
Методы расчета ферм Презентация на тему Золотое сечение-гармония математики
Презентация на тему Золотое сечение-гармония математики  Переместительный и сочетательный законы сложения
Переместительный и сочетательный законы сложения Тела вращения. Урок 142
Тела вращения. Урок 142 Элементы теории вероятностей
Элементы теории вероятностей математика гр 32 парність-2.docx
математика гр 32 парність-2.docx Презентация на тему Вычисления с многозначными числами
Презентация на тему Вычисления с многозначными числами  Деление дробей. Решение задач
Деление дробей. Решение задач Линейные алгоритмы
Линейные алгоритмы Круговая окружность
Круговая окружность Эйлеровы и гамильтоновы графы
Эйлеровы и гамильтоновы графы Возрастание и убывание функции
Возрастание и убывание функции Таблица Шульте
Таблица Шульте Планиметрия малыми порциями
Планиметрия малыми порциями Вычитание (Помоги Буратино исправить ошибки)
Вычитание (Помоги Буратино исправить ошибки)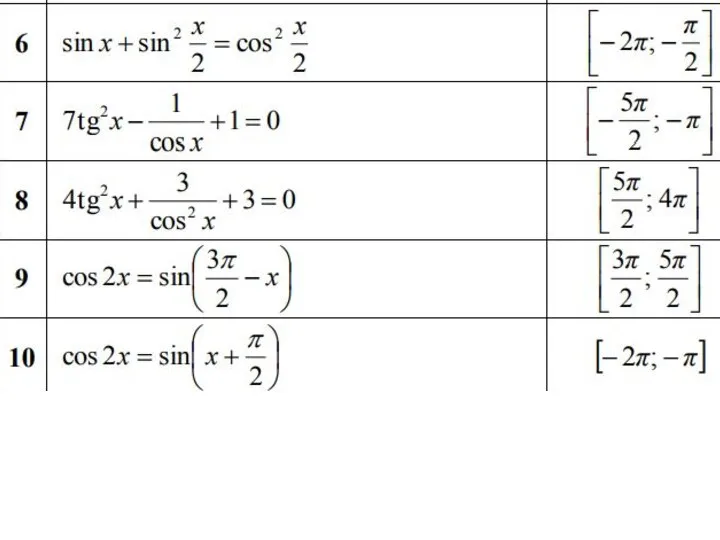 Решение уравнений
Решение уравнений 2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию
2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию Методы статистического анализа литературных текстов
Методы статистического анализа литературных текстов Прямоугольные треугольники
Прямоугольные треугольники Элективный курс. Алгебра 11 класс. Уроки 07-08
Элективный курс. Алгебра 11 класс. Уроки 07-08 Практикум №5 (вторая часть РГР). Построение эконометрических моделей нелинейной парной регрессии (НПР)
Практикум №5 (вторая часть РГР). Построение эконометрических моделей нелинейной парной регрессии (НПР) Натуральный ряд чисел
Натуральный ряд чисел Многогранный угол. Трёхгранный угол
Многогранный угол. Трёхгранный угол