Уравнения и неравенства с одной переменной

Цели и задачи:
повторить, обобщить и закрепить знания учащихся по данной теме;
подготовить учащихся к выполнению контрольной работы;
воспитывать умение слушать отвечающего, дополнять ответ и отстаивать свое мнение, если ты прав;
развивать логическое мышление, быстроту и смекалку при решении упражнений.

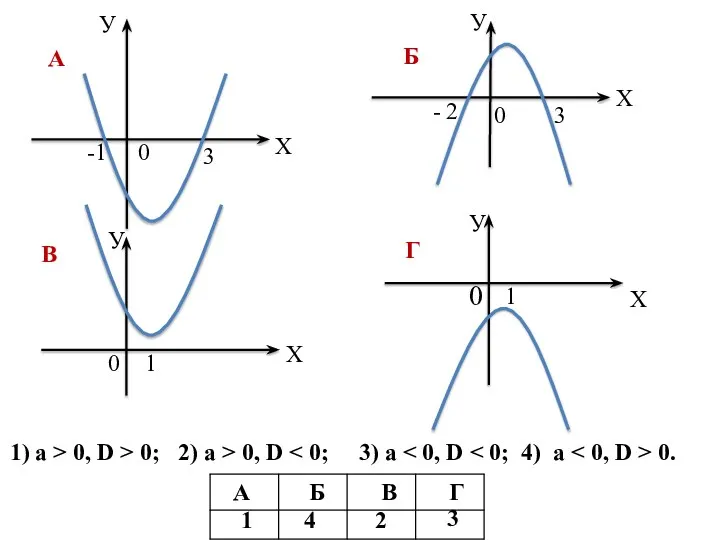
Функция f(х) = ах² + bх + с задана графически. D – дискриминант соответствующего квадратного трехчлена. Соотнесите графики с ответами и заполните таблицу, проставив в ней номера ответов.

1) a > 0, D > 0; 2) a > 0, D < 0; 3) a < 0, D < 0; 4) a < 0, D > 0.
1
4
2
3

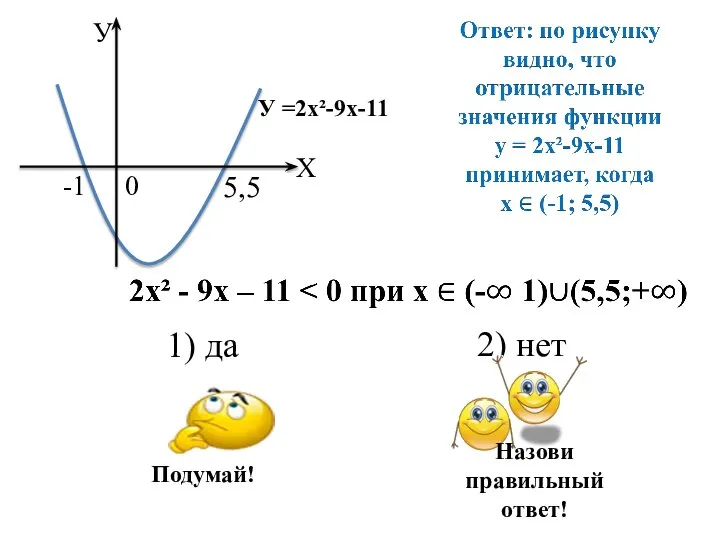
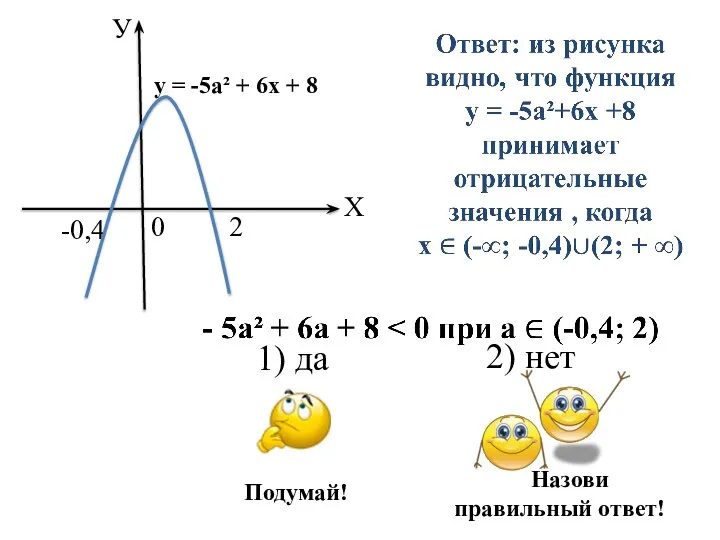
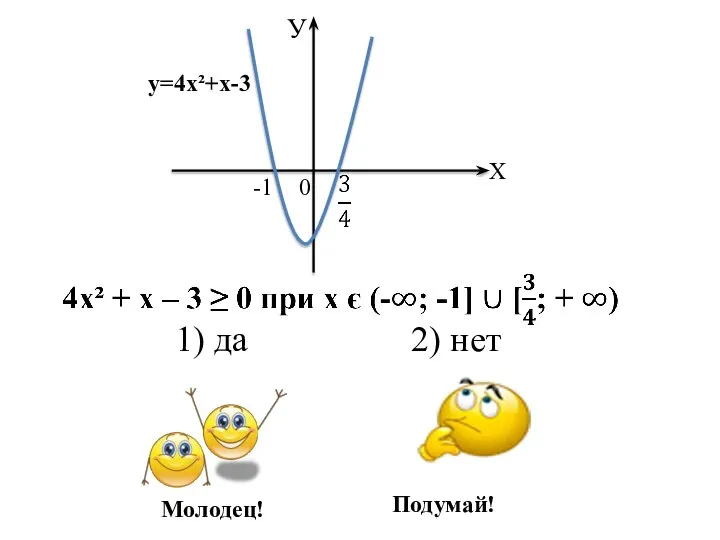
2. На рисунках изображены схематически графики функций, и с помощью этих графиков решены неравенства. Определите, верно ли они решены, выбрав ответ да или нет. Если решение неверное, надо дать правильный ответ.

1) да
2) нет

1) да
2) нет

1) да
2) нет

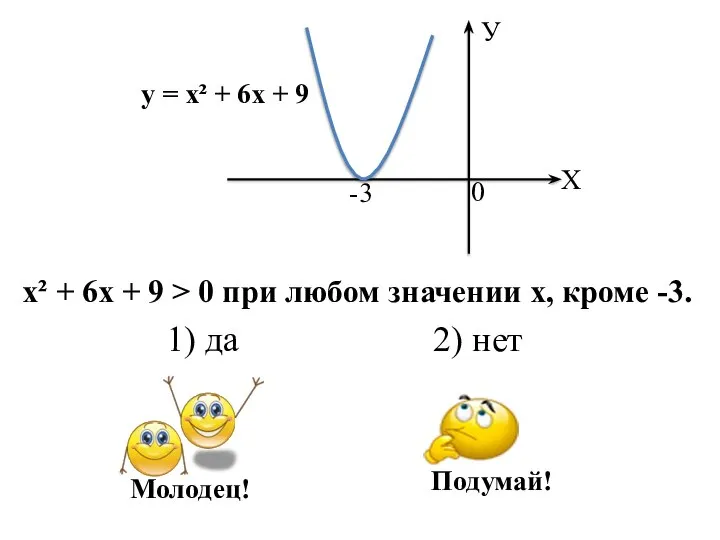
х² + 6х + 9 > 0 при любом значении х, кроме -3.
1) да
2) нет
У
Х
0
-3
у = х² + 6х + 9

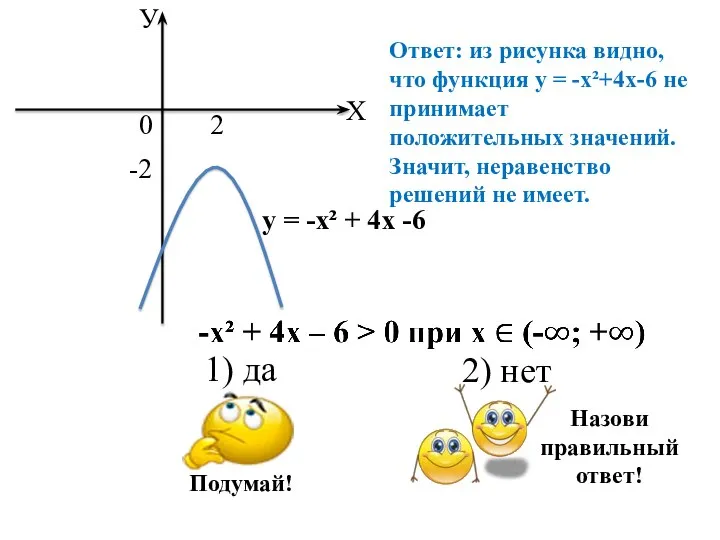
Ответ: из рисунка видно, что функция у = -х²+4х-6 не принимает положительных значений. Значит, неравенство решений не имеет.
1) да
2) нет

Решите неравенство f(х) ≤ 0
Выберите верный ответ.
4) [0; 2]
2) (- 1; 3)
1) [- 1; 3]

Решите неравенство f(х)≥0.
Выберите верный ответ.
3) [-2;3]
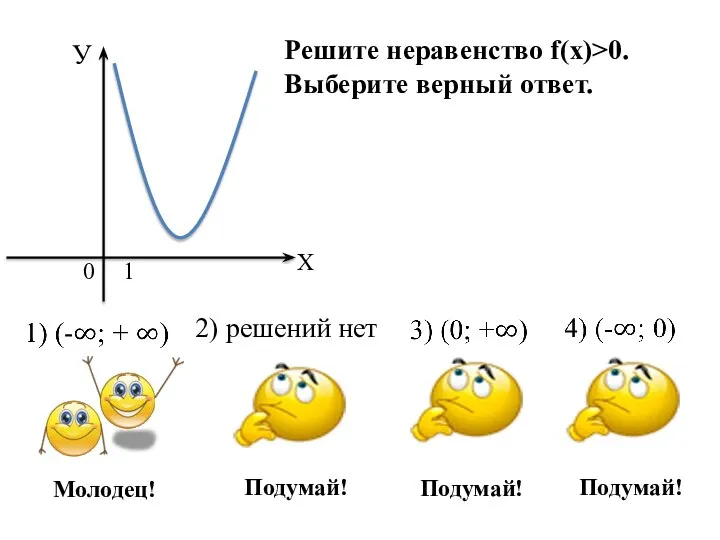
2) (-2; 3)

2) решений нет
Решите неравенство f(х)>0. Выберите верный ответ.

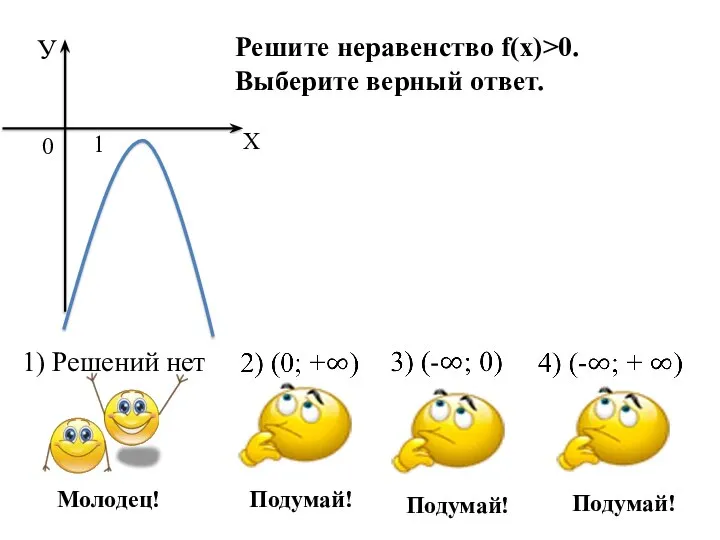
Решите неравенство f(х)>0. Выберите верный ответ.
1) Решений нет

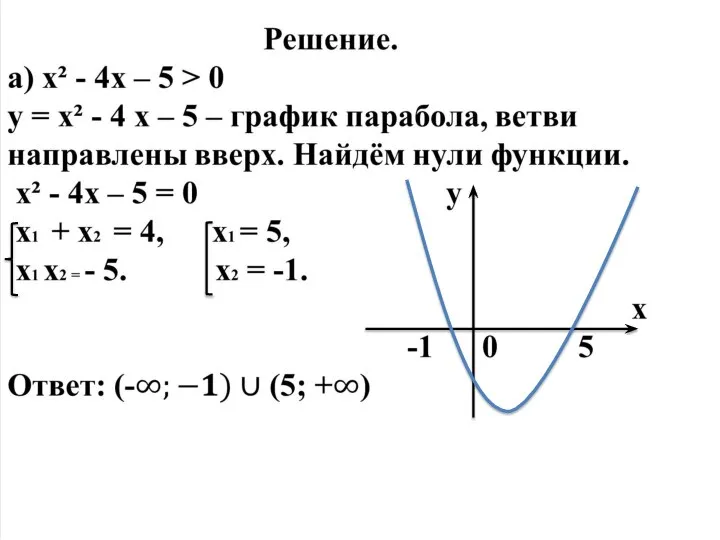
1. Решите неравенства.
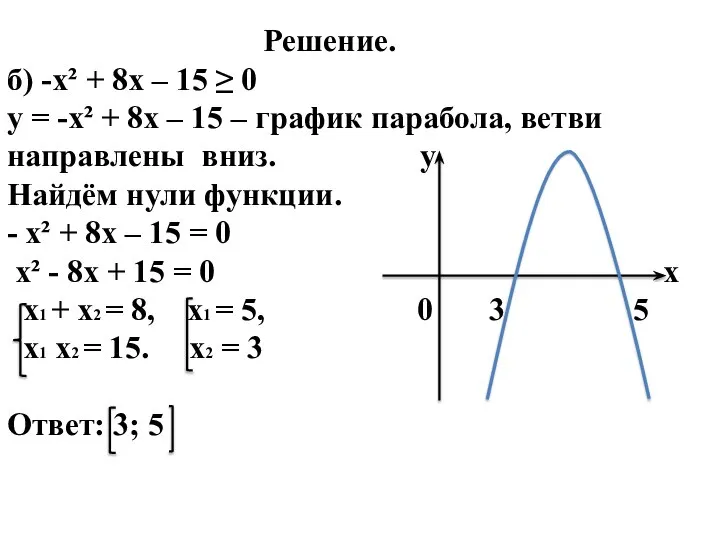
а) х² - 4х – 5 > 0; б) - х² + 8х – 15 ≥ 0.

Решение.
б) -х² + 8х – 15 ≥ 0
у = -х² + 8х – 15 – график парабола, ветви направлены вниз. у
Найдём нули функции.
- х² + 8х – 15 = 0
х² - 8х + 15 = 0 х
х1 + х2 = 8, х1 = 5, 0 3 5
х1 х2 = 15. х2 = 3
Ответ: 3; 5

Решение неравенств методом интервалов.
Ученику 9 класса Петру Иванову учитель предложил решить два неравенства методом интервалов. Он решил. Учитель проверил и сказал ему, что у него есть ошибки в ответах. Попросил его подумать и исправить.
Давайте, ребята, поможем Петру исправить ошибки.
2. Решите неравенства методом интервалов
а) (х + 2) (х – 7) > 0;
Ученик.
Решение.
а) (х + 2)(х – 7) > 0
Найдем нули функции у = (х + 2) (х – 7).
(х + 2)(х -7) = 0 + - +
Х + 2 = 0 или х – 7 = 0 - 2 7
Х = -2 х = 7
Ответ: (-2; 7)

б)(х – 5) (х + 3)≤0
Решение.
Найдем нули функции f(х)= (х – 5) (х + 3)
(х – 5) (х + 3) = 0
х – 5 = 0 или х + 3 = 0
х = 5 х = - 3
+ - +
-3 5
Ответ: ( -3; 5).
Правильный ответ: [-3; 5].

1. Решите неравенство в ответ запишите наименьшее целое решение неравенства
(х – 4) (3х +1) (х -2) > 0