Содержание
- 2. Уравнения и неравенства с параметрами Под уравнением с параметром, обычно принято понимать, уравнение вида f(x;a)=0, где
- 3. Уравнения и неравенства с параметрами Пример. Решить относительно х: а) 3а(а-3)х = а-3 б) 3а(а-3)х >
- 4. Уравнения и неравенства с параметрами б) Нам так же дано обычное линейное неравенство. В этом случае
- 5. Уравнения и неравенства с параметрами 4. 0 5. a>3 Коэффициент 3а(а-3) положителен, значит, при делении на
- 6. Уравнения и неравенства с параметрами Пример. Решить уравнение: Решение. При решении квадратных уравнений с параметром, как
- 7. Уравнения и неравенства с параметрами Перейдем ко второму случаю, найдем дискриминант нашего уравнения: Дальше следует рассуждать
- 8. Уравнения и неравенства с параметрами в) При D>0, два корня уравнения. В нашем случае, при а>-1
- 9. Уравнения и неравенства с параметрами Пример. Решить уравнение: Решение. Начнем с обычного действия, возведем обе части
- 10. Уравнения и неравенства с параметрами Перейдем к рассмотрению трех возможных случаев:
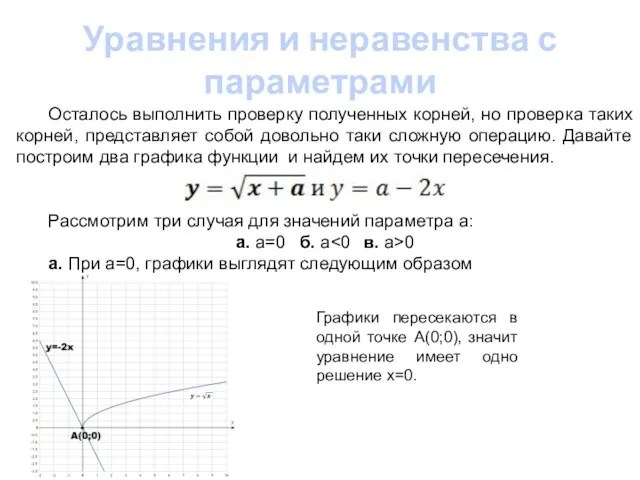
- 11. Уравнения и неравенства с параметрами Осталось выполнить проверку полученных корней, но проверка таких корней, представляет собой
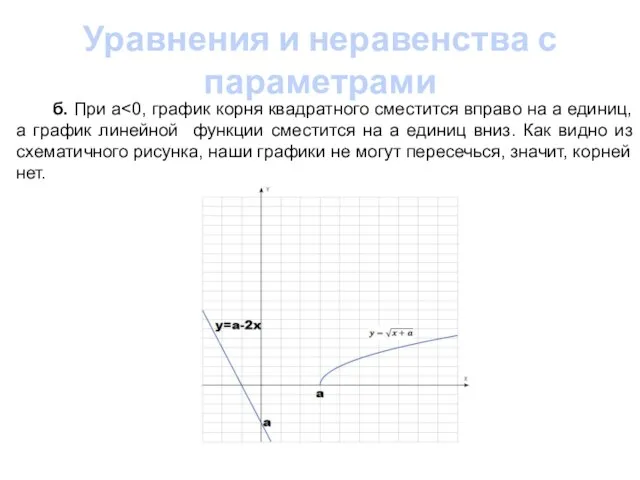
- 12. Уравнения и неравенства с параметрами б. При a
- 13. Уравнения и неравенства с параметрами в. При a>0, графики функций пересекаются в одной точке. Выше мы
- 14. Уравнения и неравенства с параметрами Мы можем заметить, что абсцисса точки пересечения больше нуля, но меньше
- 15. Уравнения и неравенства с параметрами Для уверенности в правильности решения проверим второй корень. Ответ: При а=0,
- 17. Скачать презентацию












 Вычисление интегралов вида R(x, Jax2 + bx+c) dx
Вычисление интегралов вида R(x, Jax2 + bx+c) dx Вавилонская математика
Вавилонская математика Математическая шарада
Математическая шарада Китайская математика
Китайская математика Порядок действий в вычислениях
Порядок действий в вычислениях Алгебраические действия над комплексными числами
Алгебраические действия над комплексными числами Тема 1
Тема 1 Проценты. Готовимся к ОГЭ
Проценты. Готовимся к ОГЭ Состав числа 8
Состав числа 8 Презентация на тему Предел переменной величины
Презентация на тему Предел переменной величины  Производная функции. Обобщающий урок
Производная функции. Обобщающий урок Построение графиков функций с помощью производных
Построение графиков функций с помощью производных Сравнение натуральных чисел
Сравнение натуральных чисел Величины, длина
Величины, длина Нахождение sin и tg
Нахождение sin и tg Сложение с переходом через десяток вида +2, +3, +4, +5. Считаем с гномами
Сложение с переходом через десяток вида +2, +3, +4, +5. Считаем с гномами Проценты
Проценты Методы решения систем линейных уравнений: метод сложения
Методы решения систем линейных уравнений: метод сложения Координатная плоскость
Координатная плоскость От перестановки множителей произведение не изменяется
От перестановки множителей произведение не изменяется Интеграл, интеграция, интегрирование. Решение задач
Интеграл, интеграция, интегрирование. Решение задач Переместительное свойство умножения
Переместительное свойство умножения ЕГЭ по математике. Экономические задачи VII
ЕГЭ по математике. Экономические задачи VII Тема урока: Умножение чисел на сумму
Тема урока: Умножение чисел на сумму Многоугольники и многогранники в архитектуре и живописи
Многоугольники и многогранники в архитектуре и живописи Замена числа суммой разрядных слагаемых. (дистанционное обучение)
Замена числа суммой разрядных слагаемых. (дистанционное обучение)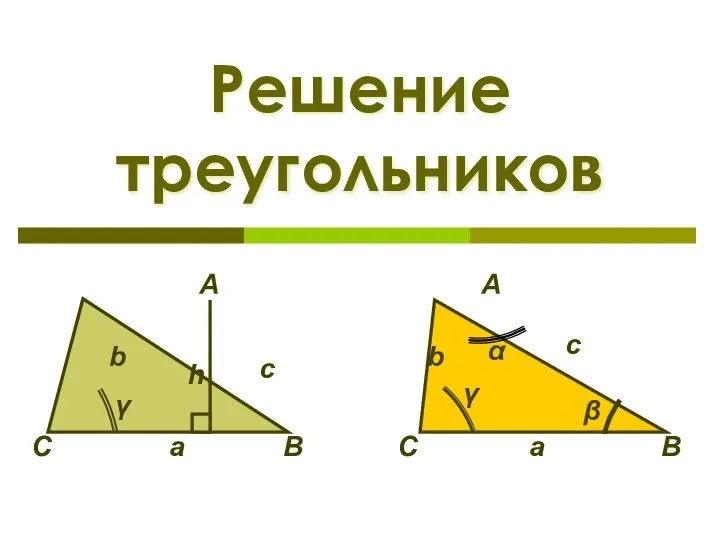 Решение треугольников
Решение треугольников Блестящая Математика: Математические Игры С Камешками марблс
Блестящая Математика: Математические Игры С Камешками марблс