Содержание
- 2. ПЛАН УРОКА: Цели урока Повторение Историческая справка Новая тема Говори правильно Закрепление
- 3. Образовательная: знакомство с понятиями наибольший общий делитель и взаимно простые числа. Развивающая: развить умение обобщать, систематизировать
- 4. ПОВТОРЕНИЕ
- 5. Вопрос 1. Какое число называют делителем данного натурального числа? Вопрос 2. Какое число называют кратным данному
- 6. Вопрос 6. Как по записи натурального числа определить, делится ли оно без остатка на 3 или
- 7. Делителем натурального числа а называют натуральное число, на которое а делится без остатка. НАЗАД
- 8. Кратным натурального числа а называют натуральное число, которое делится без остатка на а. НАЗАД
- 9. Если запись натурального числа оканчивается 0 или 5, то это число делится без остатка на 5.
- 10. Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10. Если
- 11. Если запись натурального числа оканчивается четной цифрой, то это число делится без остатка на 2. А
- 12. Если сумма цифр числа делится на 3, то и число делится на 3. Если сумма цифр
- 13. Если сумма цифр числа делится на 9, то и число делится на 9. Если сумма цифр
- 14. Натуральные числа называют простыми числами, если они имеют только два различных делителя: единицу и самого себя.
- 15. Число, имеющее более двух делителей, называется составным числом. НАЗАД
- 16. Число 1 имеет только один делитель: само это число. Поэтому его не относят ни к составным,
- 17. ИСТОРИЧЕСКАЯ СПРАВКА
- 18. Натуральное число называется ПРОСТЫМ, если оно имеет только два делителя: единицу и само это число. Интерес
- 19. ДАЛЕЕ
- 20. Древнегреческий математик Евклид в своей книге «Начала», бывшей на протяжении двух тысяч лет основным учебником математики,
- 21. Эратосфен придумал другой способ. Он записывал все числа от 1 до какого- то числа, а потом
- 22. Итак, простыми числами от 2 до 40 являются 17 чисел: 2, 3, 5, 7, 11, 13,
- 23. Лишь в XIX в., около 2200 лет после Евклида, великий русский математик Пафнутий Львович Чебышев открыл
- 24. НОВАЯ ТЕМА
- 25. ЗАДАЧА 1. Какое наибольшее число одинаковых подарков можно составить из 48 конфет «Ласточка» и 36 конфет
- 26. Видим, что наибольшим из этих чисел является 12. Его называют наибольшим общим делителем чисел 48 и
- 27. НАИБОЛЬШЕЕ НАТУРАЛЬНОЕ ЧИСЛО, НА КОТОРОЕ ДЕЛИТСЯ БЕЗ ОСТАТКА ЧИСЛА a и b, НАЗЫВАЮТ НАИБОЛЬШИМ ОБЩИМ ДЕЛИТЕЛЕМ
- 28. ЗАДАЧА 2. Найдем наибольший общий делитель чисел 24 и 35. РЕШЕНИЕ. Делителями 24 будут 1, 2,
- 29. НАТУРАЛЬНЫЕ ЧИСЛА НАЗЫВАЮТ ВЗАИМНО ПРОСТЫМИ, ЕСЛИ ИХ НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ РАВЕН 1. Записывают НОД (a, b)
- 30. Разложим на множители числа 48 и 36, и получим: 48 2 24 2 12 2 6
- 31. Чтобы найти наибольший общий делитель нескольких натуральных чисел, НАДО: Разложить их на простые множители. Из множителей,
- 32. ПРИМЕР 1. Найдите наибольший общий делитель чисел 50 и 175. 50 2 25 5 5 5
- 33. Получим: 50 = 2 · 5 · 5 175 = 5 · 5 · 7 2.
- 34. ПРИМЕР 2. Найдите наибольший общий делитель чисел 324, 111 и 432. 111 3 37 37 1
- 35. Получим: 111 = 3 · 37 324 = 2 · 2 · 3 · 3 ·
- 36. ПРИМЕР 3. Являются ли взаимно простыми числа 77 и 20? 20 2 10 2 5 5
- 37. Получим: 20 = 2 · 2 · 5 77 = 7 · 11 2. Из множителей,
- 38. ГОВОРИ ПРАВИЛЬНО
- 39. В предложениях с сочетаниями общий делитель, наибольший общий делитель числительные читают в родительном падеже, если перед
- 40. ЗАКРЕПЛЕНИЕ
- 41. ЗАДАЧА 1. Найдите наибольший общий делитель чисел 35 и 40. ЗАДАЧА 2. Найдите наибольший общий делитель
- 42. НА ЗАДАЧУ 1 НОД (35, 40) = 5. НАЗАД РЕШЕНИЕ
- 43. 35 = 5 · 7 5 · 7 = 5 НОД(35, 40) = 5 35 5
- 44. НА ЗАДАЧУ 2 НОД (612, 680) = 68. НАЗАД РЕШЕНИЕ
- 45. 612 = 2 · 2 · 3 · 3 · 17 2 · 2 · 3
- 46. НА ЗАДАЧУ 3 НОД (195, 156, 260) = 13. НАЗАД РЕШЕНИЕ
- 47. 195 = 3 · 5 · 13 3 · 5 · 13 = 13 НОД (195,
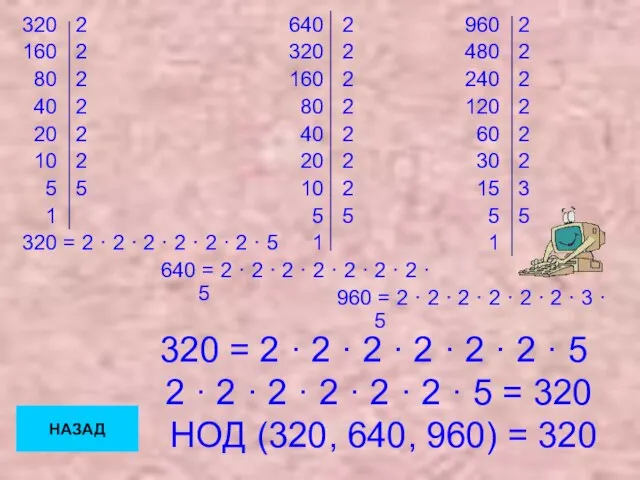
- 48. НА ЗАДАЧУ 4 НОД (320, 640, 960) = 320. НАЗАД РЕШЕНИЕ
- 49. 320 = 2 · 2 · 2 · 2 · 2 · 2 · 5 2
- 50. НА ЗАДАЧУ 5 НОД (35,88) = 1. Следовательно, числа 35 и 88 – взаимно простые. НАЗАД
- 51. 35 = 5 · 7 5 · 7 = 1 НОД (35, 88) = 1. Следовательно,
- 53. Скачать презентацию

















































 Интегральное исчисление. Функция. Предел функции
Интегральное исчисление. Функция. Предел функции Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов Презентация на тему Смежные углы
Презентация на тему Смежные углы  Множители и произведение
Множители и произведение Аппроксимация функций. Метод Лагранжа
Аппроксимация функций. Метод Лагранжа Основы тригонометрии. Радианная мера угла. Вращательное движение точки вокруг начла координат
Основы тригонометрии. Радианная мера угла. Вращательное движение точки вокруг начла координат Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Четырехзначные числа (3 класс)
Четырехзначные числа (3 класс) Помоги Незнайке выполнить задание от Знайки
Помоги Незнайке выполнить задание от Знайки Статистический образ мышления. Научная публикация. (Лекция 3)
Статистический образ мышления. Научная публикация. (Лекция 3) Числовые головоломки
Числовые головоломки Объем конуса
Объем конуса Клуб весёлых и находчивых. Турнир любителей математики
Клуб весёлых и находчивых. Турнир любителей математики Решение задач по теме: Прямоугольник. Ромб. Квадрат
Решение задач по теме: Прямоугольник. Ромб. Квадрат Булева алгебра
Булева алгебра Правильные многогранники
Правильные многогранники Несобственные интегралы первого рода
Несобственные интегралы первого рода Прикладной количественный анализ заголовков
Прикладной количественный анализ заголовков Эквивалентные преобразования матриц
Эквивалентные преобразования матриц Таблица значений синуса и тангенса для углов
Таблица значений синуса и тангенса для углов Решение задач
Решение задач Ariile figurilor geometrice plane
Ariile figurilor geometrice plane Презентация на тему ИЗМЕРЕНИЕ ОТРЕЗКОВ
Презентация на тему ИЗМЕРЕНИЕ ОТРЕЗКОВ  Высота, биссектриса и медиана треугольника
Высота, биссектриса и медиана треугольника По следам теоремы Пифагора
По следам теоремы Пифагора Функция
Функция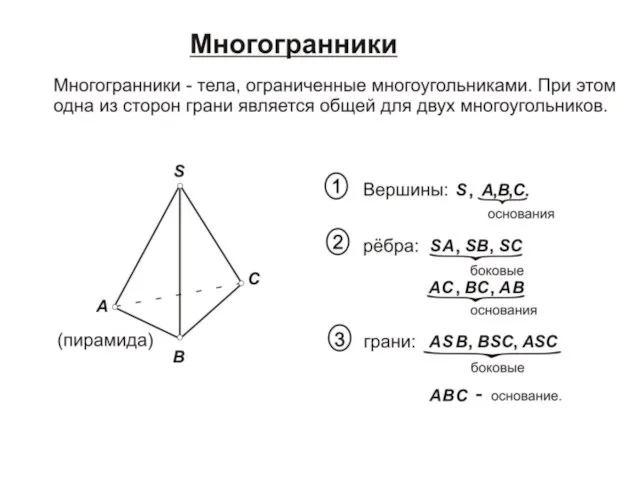 Многогранники + точки. Лекция 5
Многогранники + точки. Лекция 5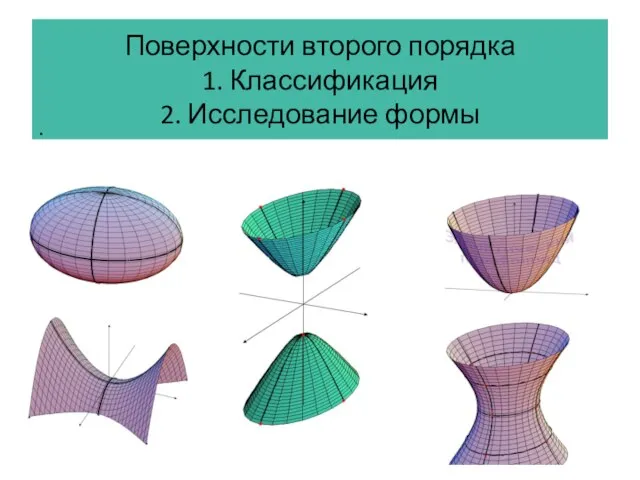 Поверхности второго порядка
Поверхности второго порядка