- Главная
- Математика
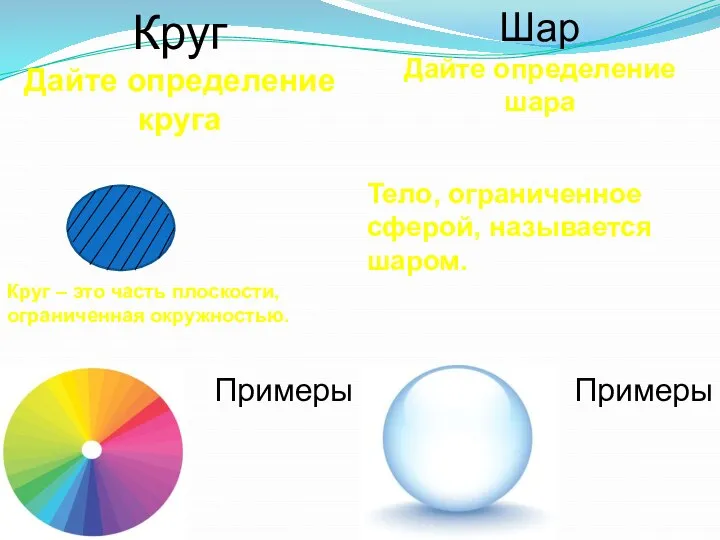
- Симметрия в пространстве. Уравнение Сферы

Содержание
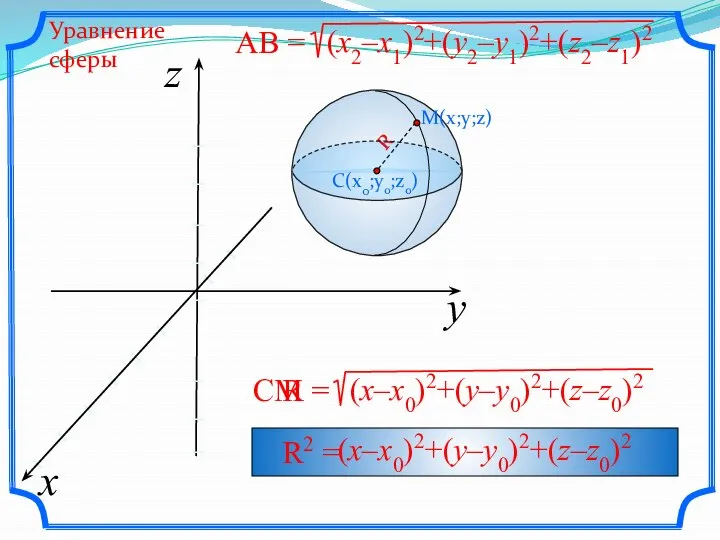
Слайд 3т.О – центр сферы;
R – радиус сферы;
АВ – диаметр сферы – отрезок,
т.О – центр сферы;
R – радиус сферы;
АВ – диаметр сферы – отрезок,

соединяющий две точки сферы и проходящий через её центр.
А, В – диаметрально противоположные точки шара.
А, В – диаметрально противоположные точки шара.
http://lapinagv.jimdo.com/
Слайд 6Вывести уравнение сферы с центром в начале координат
x²+y²+z²=R²
Вывести уравнение сферы с центром в начале координат
x²+y²+z²=R²

- Предыдущая
КлассицизмСледующая -
Кокосовая пальма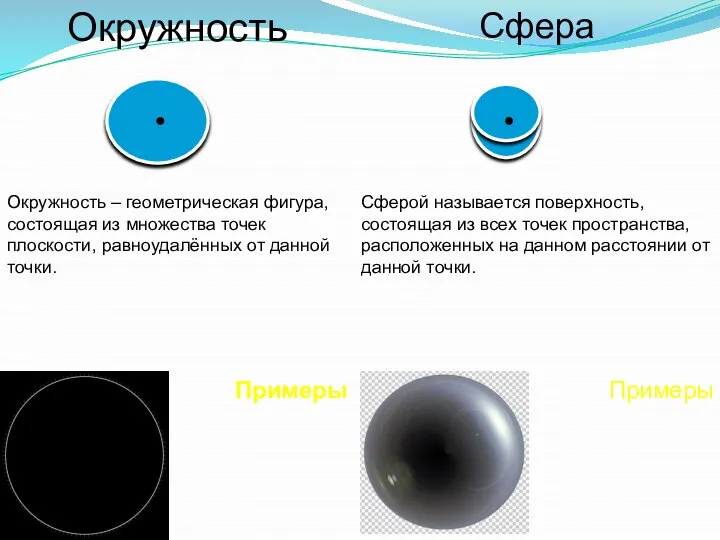
 Математика ЕГЭ. Треугольники
Математика ЕГЭ. Треугольники Математическое путешествие в мир гармонии. Устный журнал
Математическое путешествие в мир гармонии. Устный журнал Замена переменных в двойных интегралах
Замена переменных в двойных интегралах Логика высказываний. Таблица истинности логических союзов
Логика высказываний. Таблица истинности логических союзов Параллелограмм и трапеция. Урок 8
Параллелограмм и трапеция. Урок 8 Дисперсионный анализ
Дисперсионный анализ Преобразования дробей
Преобразования дробей Выражение (для печатной и электронной формы учебника)
Выражение (для печатной и электронной формы учебника) Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Среднее арифметическое
Среднее арифметическое Классная работа. Признаки равенства треугольников
Классная работа. Признаки равенства треугольников Графики функций
Графики функций Предел функции в точке
Предел функции в точке Математические основы теории искусственных нейронных сетей
Математические основы теории искусственных нейронных сетей Обработка данных. Задачи локального и глобального интерполирования
Обработка данных. Задачи локального и глобального интерполирования Симметрия. Симметричные объекты. Платоновы тела
Симметрия. Симметричные объекты. Платоновы тела Функция
Функция Формування математчних моделей електронних кіл
Формування математчних моделей електронних кіл Функции. Их свойства
Функции. Их свойства Математические модели в науке как средство работы с информацией, её представления и обработки
Математические модели в науке как средство работы с информацией, её представления и обработки Презентация на тему Круговые диаграммы (5 класс)
Презентация на тему Круговые диаграммы (5 класс)  Теория вероятности. Сокращение дробей
Теория вероятности. Сокращение дробей Дидактикалык ойындар
Дидактикалык ойындар Решение задач на проценты
Решение задач на проценты Виды треугольников
Виды треугольников Решение неоднородных систем линейных алгебраических уравнений. Семинар 3
Решение неоднородных систем линейных алгебраических уравнений. Семинар 3 Логические схемы
Логические схемы Признаки существования предела
Признаки существования предела