Содержание
- 2. Для показательной функции, как и для многих других, существует обратная функция. Однако для ее изучения сперва
- 4. Понятие логарифма Великий ученый Пьер-Симон Лаплас говорил, что изобретение логарифмов продлило жизнь астрономов вдвое, ведь с
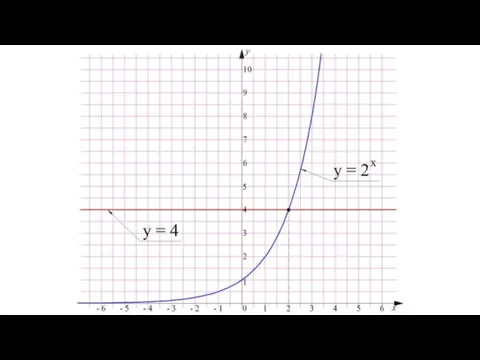
- 5. Рассмотрим простейшее показательное уравнение 2^х = 4. Так как 2^2 =4, то, очевидно, оно имеет единственный
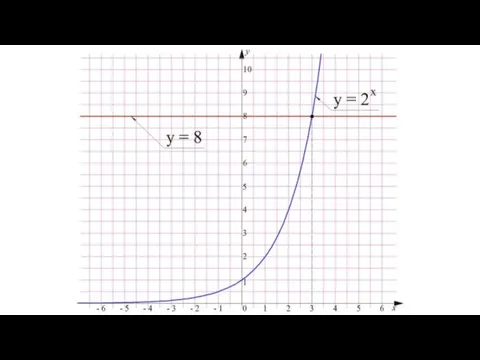
- 7. Далее посмотрим на уравнение 2^х = 8. Так как восьмерка – это двойка в кубе (2^3
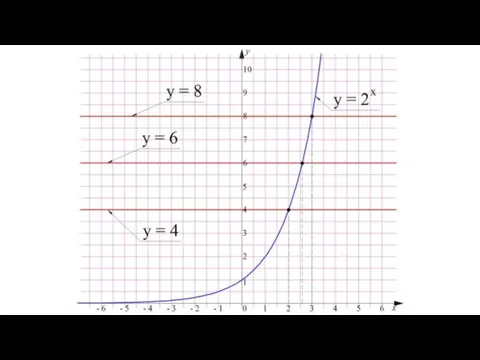
- 9. Однако если мы попытаемся решить уравнение 2^х = 6, то мы столкнемся с проблемами. Представить шестерку
- 11. Можно доказать (мы не будем этого делать), что искомый нами корень невозможно выразить с помощью дробей
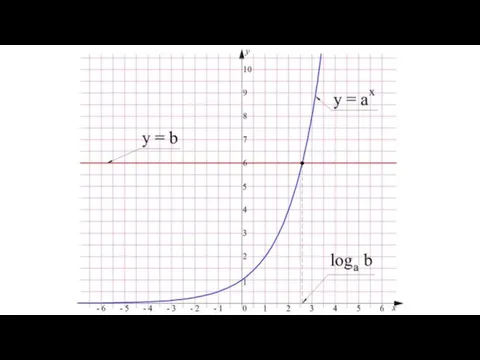
- 12. Рассмотрим теперь более общий случай. Пусть есть некоторое уравнение
- 13. Если число b положительно, то уравнение имеет корень, и при том единственный. Для его обозначения используется
- 15. Дадим строгое определение логарифма:
- 16. Задание. Какое число является решением показательного уравнения
- 17. Задача. Слиток радиоактивного изотопа, чей период полураспада (его обозначают буквой Т) составляет 10 минут, имеет начальную
- 18. Решение. Подставим исходные данные в формулу, и получим уравнение с неизвестной величиной t: 0,2 = 1•2^–t/10
- 19. Умножаем ур-ние на (– 10) и получаем: t = – 10 log2 0,3 С помощью калькулятора
- 20. Иногда бывает удобнее использовать иное определение, которое по своей сути почти не отличается от первого:
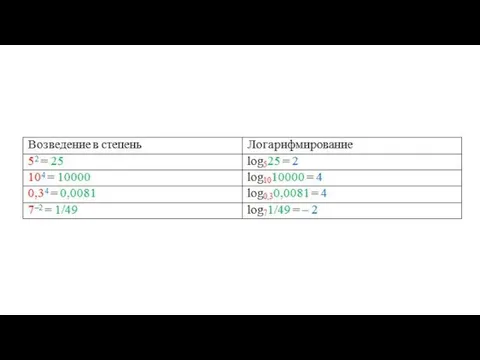
- 21. Вычислим для примера несколько простейших логарифмов:
- 22. Ограничения, связанные с логарифмом Заметим, что сам логарифм может оказаться любым вещественным числом, ведь мы умеем
- 23. Напомним, что при определении показательной функции у = а^х было введено ограничение, согласно которому основание степени
- 24. Также напомним, что показательное уравнение а^х = b имеет решение только при положительных значениях b. Это
- 25. Сформулируем эти ограничения в виде одного правила:
- 26. Ранее мы уже сталкивались с тремя случаями, когда выражения не имеют смысла. Во-первых, это происходит при
- 27. Сейчас мы узнали четвертый подобный случай, связанный с понятием логарифма. Больше в рамках курса не будут
- 28. Основные свойства логарифмов Любое число, возведенной в первую степень, равно самому себе. То есть справедливо равенство
- 29. Продемонстрируем использование этого правила:
- 30. Любое число при возведении в нулевую степень равно единице: Из этого следует второе важное правило: логарифм
- 31. Покажем несколько примеров использования этого тривиального правила:
- 32. Для получения третьего свойства логарифма запишем очевидно справедливое равенство: Пользуясь определением логарифма, мы можем записать, что
- 33. Продемонстрируем, как работает это свойство логарифмов:
- 34. Это правило можно применить для вычисления некоторых простейших логарифмов:
- 35. Логарифм logab, согласно одному из своих определений, это та степень, в которую нужно возвести а, чтобы
- 36. В силу этого тождества справедливы следующие равенства:
- 37. Функция логарифма Арифметическое действие, в ходе которого находят логарифм какого-либо числа, называется логарифмированием. Это действие является
- 39. Теперь подумаем о функции у = logax. Так как логарифмирование является обратным действием для возведения в
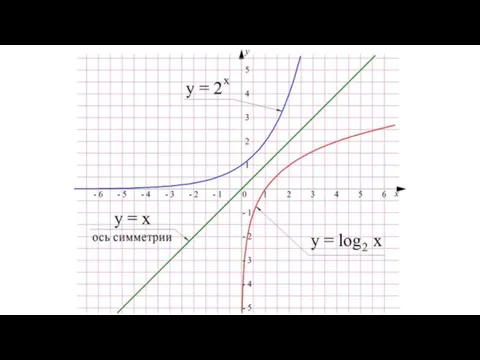
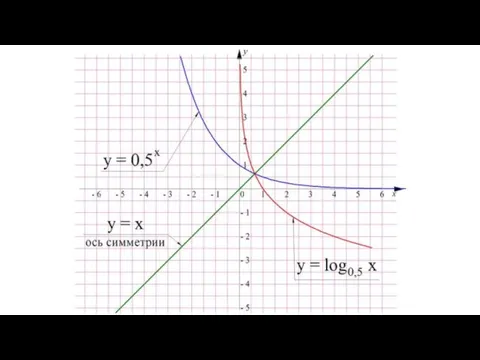
- 40. В свою очередь это означает, что графики этих двух функций должны быть симметричны относительно прямой, задаваемой
- 41. Напомним, что на вид показательной функции у = а^х влияет значение основания степени а. Если оно
- 44. Полученный график логарифмической функции называют логарифмической кривой, однако понятно, что она представляет собой всё ту же
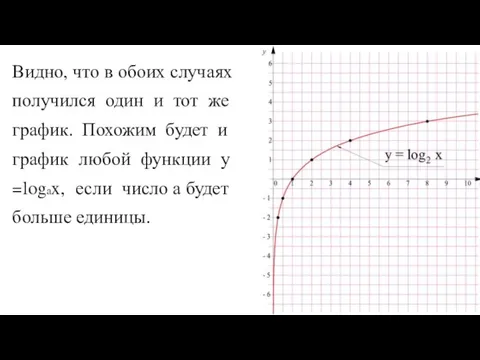
- 45. График у = log2x можно и построить иначе, по точкам, просто вычислив ее значение в нескольких
- 46. Видно, что в обоих случаях получился один и тот же график. Похожим будет и график любой
- 47. Ситуация меняется в том случае, когда а
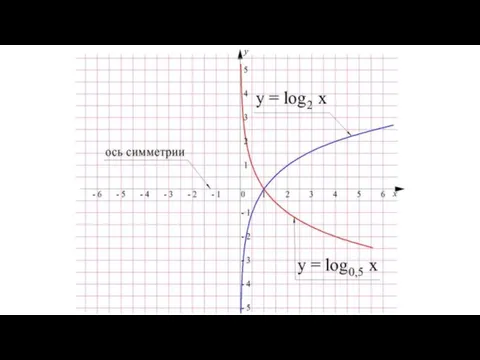
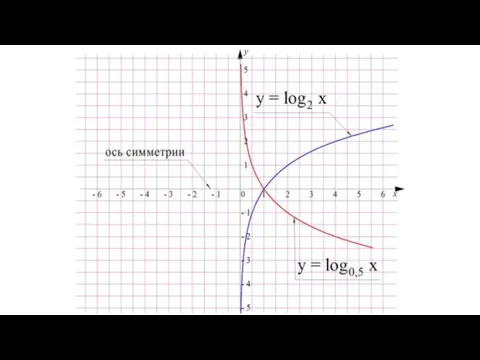
- 49. Возможно, вы заметили, что графики у = log2x и у = log0,5x чем-то похожи друг на
- 51. Причиной такой симметрии является то, что их основания, числа 2 и 0,5, являются обратными числами, то
- 52. Аналогично такой же симметрией будут обладать любые две логарифмические кривые с обратными основаниями. Это свойство логарифмов
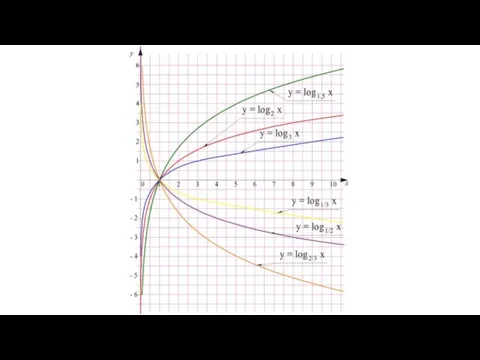
- 54. Анализируя полученные графики, мы можем заметить следующие свойства функции логарифма: Область определения логарифмической функции – это
- 55. Логарифмическая функция является строго монотонной. При этом при основании а > 1 она возрастает, а при
- 56. Три основных вида логарифмов Математика изучает логарифмы с любыми положительными основаниями. Однако на практике наиболее распространены
- 57. Первым из них является десятичный логарифм, основание которого равно 10. Дело в том, что его помощью
- 58. История понятия логарифма начиналась в XVI-XVII веках и была связана именно с необходимостью выполнения сложных арифметических
- 59. Сегодня из-за развития электроники десятичные логарифмы используются значительно реже по сравнению с 50-60 г. XX века.
- 60. Наконец, самым важным является натуральный логарифм. Это логарифм, основанием которого является число e, примерно равное 2,71828…
- 61. Свойства натурального логарифма, которые отличают его от других логарифмов, будут изучены нами позднее. Заметим лишь, что
- 62. Преобразования логарифмических выражений Для работы с логарифмическими выражениями надо знать несколько основных свойств логарифмов. Первое из
- 63. Для доказательства этого правила введем обозначения. Пусть Тогда нам надо доказать, что z = x +
- 64. Теперь подставим (1) и (2) в (3): Получили, что a^z = a^x+y. В этом равенстве в
- 65. Убедимся в справедливости этого правила на простейшем примере. Очевидно, что log2 4 = 2, ведь 2^2
- 66. С другой стороны, число 32 можно представить как произведение 4•8, то есть log2 32 = log2
- 67. Покажем несколько примеров использования только что доказанного правила: Отдельно отметить, что правило сложения логарифмов действует и
- 68. Второе правило используют для определения логарифма от степени какого-либо числа.
- 69. Грубо говоря, показатель степени можно перенести и записать перед знаком логарифма. Сначала для наглядности приведем доказательство
- 71. Однако более строгое доказательство должно рассматривать и случай, когда r – это отрицательное или даже дробное
- 72. Из определения логарифма следуют следующие формулы: Подставляя первую формулу во вторую, получаем: И снова, если у
- 73. Продемонстрируем, как работает это свойство логарифмов: Правило работает и в обратную сторону:
- 74. Задание. Чему равна дробь
- 75. Третье правило помогает вычислять логарифм от частного или дроби.
- 76. Для доказательства этого свойства логарифмов воспользуемся уже доказанными нами двумя правилами. Но предварительно напомним, что произвольное
- 77. С помощью полученной формулы возможно выполнить следующие преобразования:
- 78. Заметим, что все полученные формулы справедливы только в том случае, когда под знаком логарифма стоят исключительно
- 79. Но что делать в случае, если необходимо упростить выражение с переменными, которые могут принимать как положительные,
- 80. Здесь может помочь использование модуля числа. Запись уже будет корректной при любых допустимых значениях х и
- 81. Аналогично и формулу разности логарифмов можно представить в более общем случае, при котором допускаются отрицательные значения
- 82. Можно ли записать равенство logaх^2 = 2logaх, если допускается, что х может быть и отрицательным? Нет,
- 83. Аналогичным образом можно упростить и любые другие логарифмы, аргументы которых возведены в четную степень:
- 84. Ещё раз уточним, что эти правила используются при упрощении выражений с переменными, если те могут принимать
- 85. Переход к новому основанию алгоритма До этого мы рассматривали преобразования, в ходе которых не менялось основание
- 86. Так как основания двух логарифмов различны, то мы не можем использовать выведенную нами формулу разности логарифмов.
- 87. Докажем это утверждение. Для этого введем новые переменные: Тогда по определению логарифма можно записать равенства
- 88. Отсюда следует, что a^x = c^y. Подставим в это равенство вместо а выражение c^z и получим:
- 89. Вернемся к примеру Теперь мы можем произвести эти вычисления, но для этого сначала приведем log259 к
- 90. Теперь можно вычислить, чему равна искомая разность: Формула перехода к новому основанию позволяет иначе взглянуть на
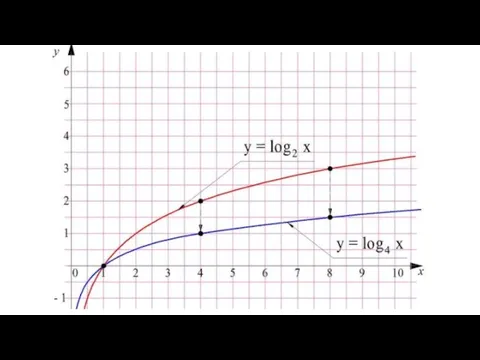
- 91. Выходит, что график у = log4x можно получить из графика у = log2x его сжатием в
- 93. Заметим, что и более общем случае графики функций у = logax и у = logbx могут
- 94. Теперь подставим вместо числа b переменную х и получим соотношение, связывающее любые две логарифмические функции: В
- 96. Попытаемся привести логарифм logab к обратному основанию, то есть к основанию 1/а: Итак, logab = –
- 98. Покажем примеры использования этой формулы: А что будет, если мы попробуем logab привести к основанию b?
- 99. Получили ещё одну замечательную логарифмическую формулу. Её работу иллюстрируют следующие примеры:
- 100. Ещё одна логарифмическая формула позволяет возводить основание логарифма и его аргумент в одинаковую степень:
- 101. Докажем это тождество в «обратном порядке», то есть из правой части выведем левую. Для этого просто
- 102. Использование логарифма для вычислений Исторически развитие теории логарифмов было связано с необходимостью выполнять громоздкие вычисления. Например,
- 103. Напомним, что десятичный логарифм обозначают символом lg, поэтому перепишем это равенство в более привычном виде: Степень
- 104. Значение числа lg 7 можно узнать с помощью калькулятора, в древности же использовали специальные таблицы, в
- 106. Получили число, записанное в стандартном виде. При этом наши расчеты были относительно простыми, если сравнить их
- 107. Логарифмическая функция в природе и науке Логарифм – это не просто инструмент для выполнения сложных операций.
- 108. В компьютерной технике многие величин можно вычислить с использованием логарифмов. Например, ясно, что чем больше телефонных
- 109. Огромное значение логарифмы имеют в астрономии. Так, яркость звезд на небе характеризуется таким параметром, как «видимая
- 110. Используются логарифмы и в термодинамике для вычисления такой характеристики систем, как энтропия. При расчете количества топлива,
- 111. В биологии давно замечено, что зависимость человеческих ощущений от силы воздействующих на них факторов окружающей среды
- 113. Скачать презентацию

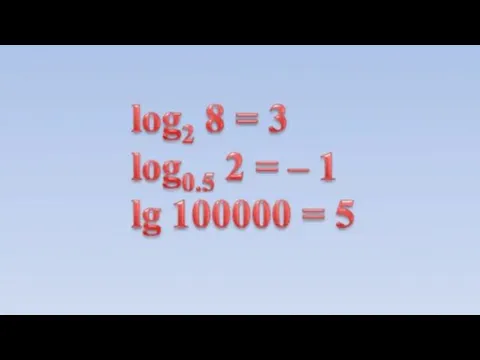
































































































 Презентация на тему Окружность, ее центр и радиус
Презентация на тему Окружность, ее центр и радиус  Алгебра высказываний
Алгебра высказываний Презентация на тему Подготовка к контрольной работе по алгебре
Презентация на тему Подготовка к контрольной работе по алгебре  Соотношения между сторонами и углами в прямоугольном треугольнике
Соотношения между сторонами и углами в прямоугольном треугольнике Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Презентация на тему Задачи на проценты
Презентация на тему Задачи на проценты  Занимательная математика
Занимательная математика Окружность в аксонометрии. 8 класс
Окружность в аксонометрии. 8 класс Презентация на тему Чётные и нечётные функции
Презентация на тему Чётные и нечётные функции  Умножение натуральных чисел
Умножение натуральных чисел Квадратные и рациональные уравнения
Квадратные и рациональные уравнения Многоугольник тетраэдр
Многоугольник тетраэдр Презентация мера угла, синус, косинус
Презентация мера угла, синус, косинус Презентация на тему Софья Васильевна Ковалевская
Презентация на тему Софья Васильевна Ковалевская  Работа над ошибками. Неполные квадратные уравнения
Работа над ошибками. Неполные квадратные уравнения История счета и систем счисления
История счета и систем счисления Функция и построение графика
Функция и построение графика Письменное умножение и деление
Письменное умножение и деление Лекция 2
Лекция 2 Чётность и нечётность, периодичность тригонометрических функций с изменениями
Чётность и нечётность, периодичность тригонометрических функций с изменениями Предельные теоремы ТВ
Предельные теоремы ТВ Функции многих переменных. Лекция 16
Функции многих переменных. Лекция 16 Второй и третий признаки равенства треугольников
Второй и третий признаки равенства треугольников Презентация на тему Параллелепипед и его объем
Презентация на тему Параллелепипед и его объем  Презентация на тему Параллелограмм и трапеция (8 класс)
Презентация на тему Параллелограмм и трапеция (8 класс)  Решение показательных неравенств
Решение показательных неравенств Симметрия
Симметрия Чтение и запись многозначных чисел. Класс миллионов. Класс миллиардов
Чтение и запись многозначных чисел. Класс миллионов. Класс миллиардов