Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики

Урок по алгебре для 9 класса по учебнику Ю.Н.Макарычев, Н.Г.Миндюк, К.И. Нешков «Алгебра 9»
с углубленным изучением математики.

Тема раздела: «Свойства функций»

Урок № 1
Тема урока: «Возрастание и убывание функций»
Тип урока: урок изучения и применения нового материала.

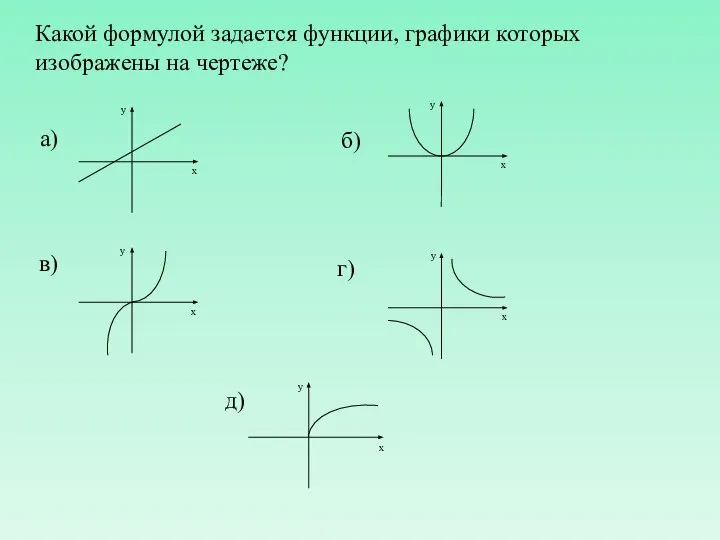
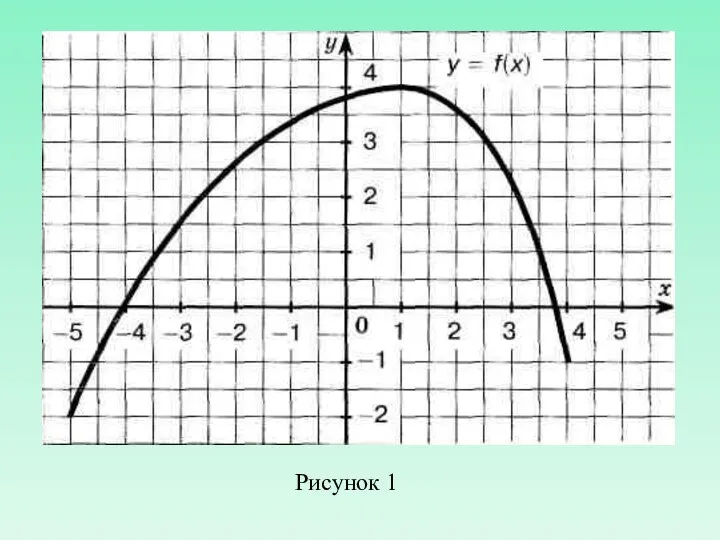
Какой формулой задается функции, графики которых изображены на чертеже?

Рисунок 1

Эталоны:
1.Функция f(x) называется возрастающей на множестве X, если для любых двух значений аргумента x1 и x2 множества X, таких, что х2 > х1, выполняется неравенство f (х2)>f (х1).
2.Функция f(х) называется убывающей на множестве Х, если для любых двух значений аргумента х2 > х1, выполняется неравенство f(х2) < f (x1).
3.Функцию, возрастающую на множестве Х или убывающую на множестве Х, называют монотонной на множестве Х.

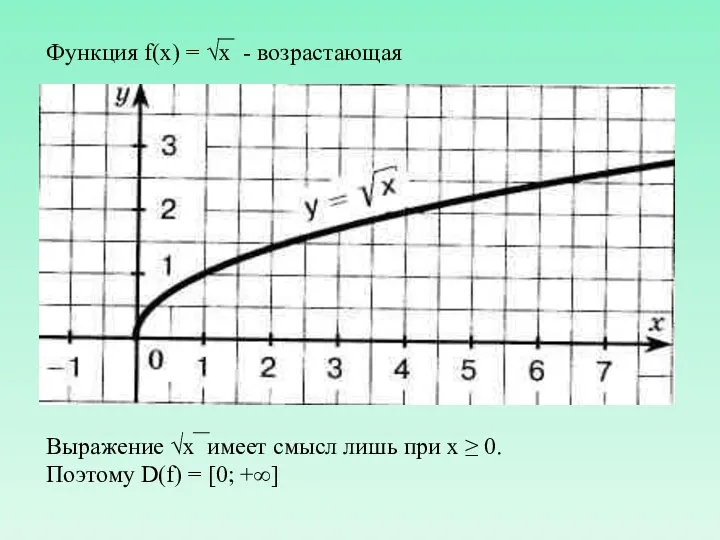
Функция f(x) = √x - возрастающая

Числитель и знаменатель дроби - положительные числа. Это следует из того, что х2 ≥ х1 ≥ 0, √x2 ≥ 0 и √x1 ≥ 0, т. е. f(x2) > f(x1). Поэтому функция f -возрастающая.

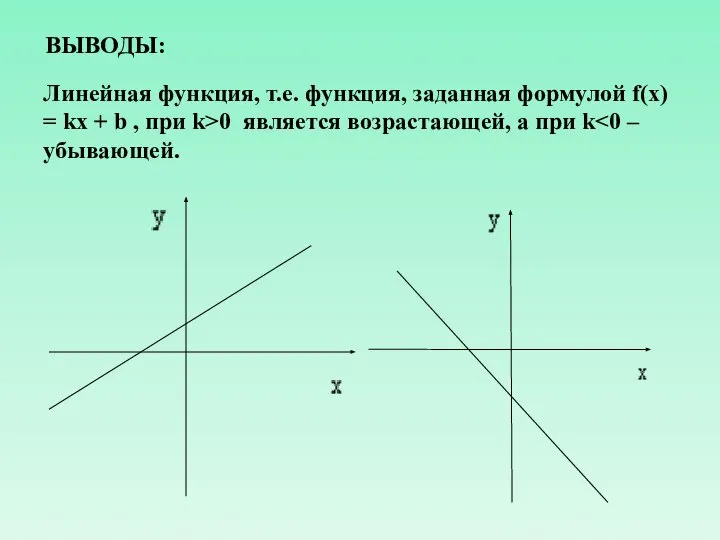
ВЫВОДЫ:
Линейная функция, т.е. функция, заданная формулой f(x) = kx + b , при k>0 является возрастающей, а при k<0 – убывающей.

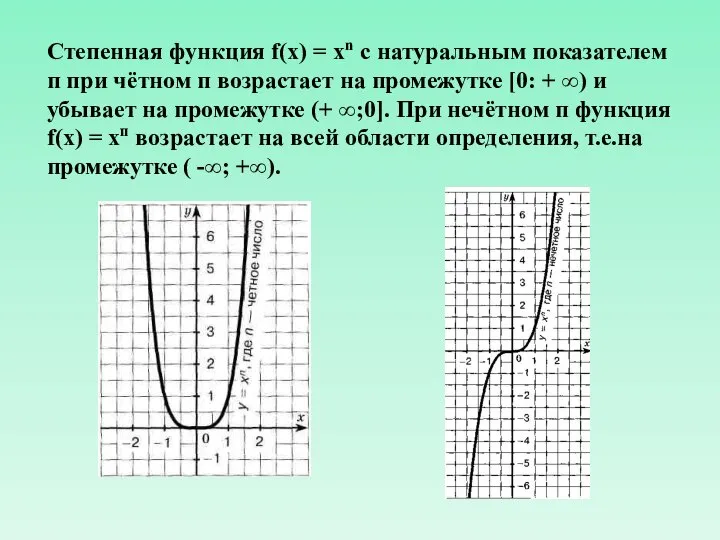
Степенная функция f(x) = xn с натуральным показателем п при чётном п возрастает на промежутке [0: + ∞) и убывает на промежутке (+ ∞;0]. При нечётном п функция f(x) = xп возрастает на всей области определения, т.е.на промежутке ( -∞; +∞).

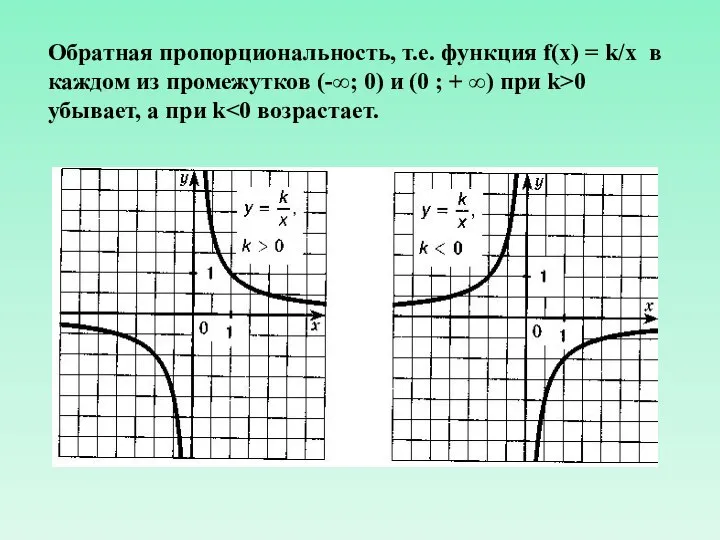
Обратная пропорциональность, т.е. функция f(x) = k/x в каждом из промежутков (-∞; 0) и (0 ; + ∞) при k>0 убывает, а при k<0 возрастает.

1.Монотонная функция каждое своё значение принимает лишь при одном значении аргумента.
Свойства монотонных функций :
.Если функция y = f(x) монотонна на множестве X и сохраняет на этом множестве знак, то функция g(x) = 1/f(x) на множестве X имеет противоположный характер монотонности.
.Если функция y = f(x) является возрастающей (убывающей), то функция y = - f(x) является убывающей (возрастающей).
.Сумма двух возрастающих функций является возрастающей функцией, а сумма двух убывающих функций является убывающей функцией.
.Если обе функции f и g возрастающие или обе убывающие, то функция φ(x) = f(g(x)) – возрастающая функция.

Решите уравнение :
X5 + X3 + X = - 42

Контрольные вопросы:
♦ Сформулируйте определение возрас - тающей и убывающей функций на мно - жестве Х.
♦ Какая функция называется монотонной на множестве Х.
♦ Приведите примеры возрастающей и убывающей функций.