Содержание
- 2. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ -способность систем слабо менять (в том или ином смысле) своё состояние или свойства под
- 3. Основные понятия: Пусть траектория L динамической системы задаётся отображением х(t) = Тtх0, где х-совокупность координат точки
- 4. Траектория L у с т о й ч и в а п о Л я п
- 5. Для исследования У. обычно применяют два метода Ляпунова. П е р в ы й (или п
- 6. т. е. V убывает на любой траектории системы, кроме тех, к-рые отвечают стационарным состояниям (x=-w. 0,
- 7. Теорема Ляпунова об устойчивости по первому приближению Пусть 1) непрерывны и непрерывно дифференцируемы по , 2)
- 8. Фазовая плоскость — координатная плоскость, в которой по осям координат откладываются какие-либо две переменные (фазовые координаты),
- 10. Изменение состояния системы отображается на фазовой плоскости движением этой точки. След от движения изображающей точки называется
- 11. Классификация точек Рассмотрим систему двух линейных дифференциальных уравнений с постоянными коэффициентами Характеристическое уравнение этой системы имеет
- 12. Рассмотрим следующие возможные случаи: 1) Корни характеристического уравнения действительные, отрицательные и различные. Точка покоя будет устойчива.
- 13. 2) Корни характеристического уравнения действительны и или В этом случае точка покоя также будет устойчива. или
- 15. Скачать презентацию












 Устный счёт для дошкольников
Устный счёт для дошкольников Больше, меньше, столько же
Больше, меньше, столько же Юность Великих математиков. 5 класс
Юность Великих математиков. 5 класс Односторонние пределы
Односторонние пределы Функция
Функция Признак параллельности прямых по равенству соответственных углов
Признак параллельности прямых по равенству соответственных углов Вероятностные задачи
Вероятностные задачи Решение задач (1 класс)
Решение задач (1 класс) Область визначення функції
Область визначення функції Площади и объемы многогранников. Решение задач
Площади и объемы многогранников. Решение задач Сравнение числовых выражений (Урок 30)
Сравнение числовых выражений (Урок 30) Сложение отрицательных чисел
Сложение отрицательных чисел Приёмы устных вычислений вида 240 ● 4, 203 ● 4, 960 : 3
Приёмы устных вычислений вида 240 ● 4, 203 ● 4, 960 : 3 Решение треугольников
Решение треугольников Средние величины в юридической статистике
Средние величины в юридической статистике HMM выравнивание
HMM выравнивание Задачи по математике. Урок 3
Задачи по математике. Урок 3 Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Великие математики
Великие математики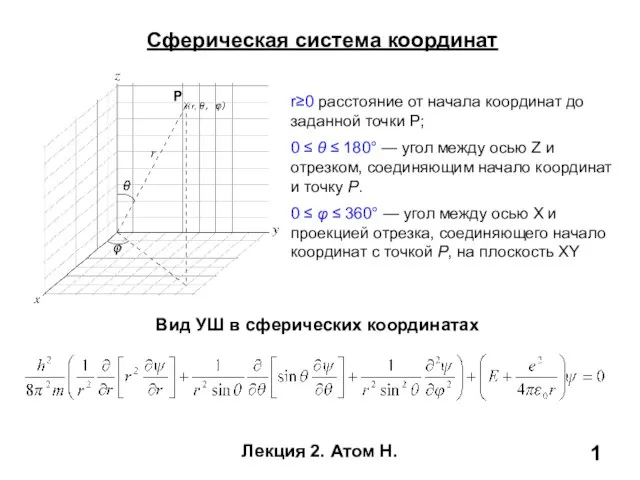 Сферическая система координат
Сферическая система координат Игра по станциям математический турнир. 7 класс
Игра по станциям математический турнир. 7 класс Уравнение прямой
Уравнение прямой Логарифмические уравнения
Логарифмические уравнения Таблица истинности
Таблица истинности Подготовка к ВПР (8 класс)
Подготовка к ВПР (8 класс) Многоугольники в жизни. Примеры
Многоугольники в жизни. Примеры Углы. Тест
Углы. Тест Контрольная работа по алгебре
Контрольная работа по алгебре