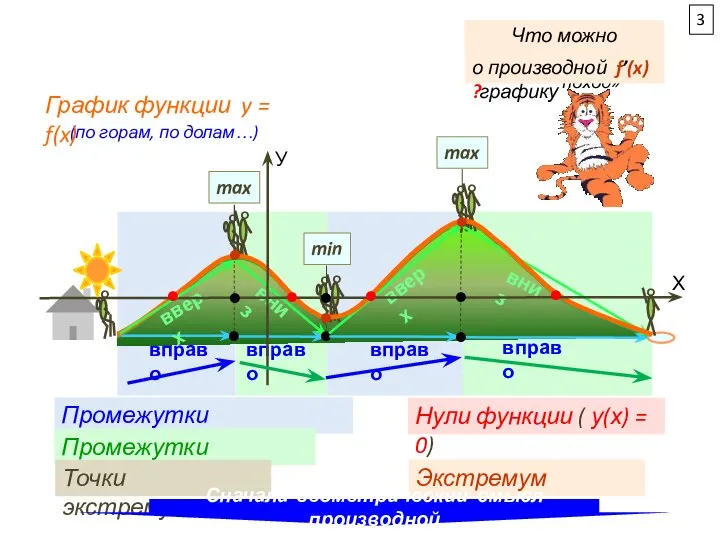
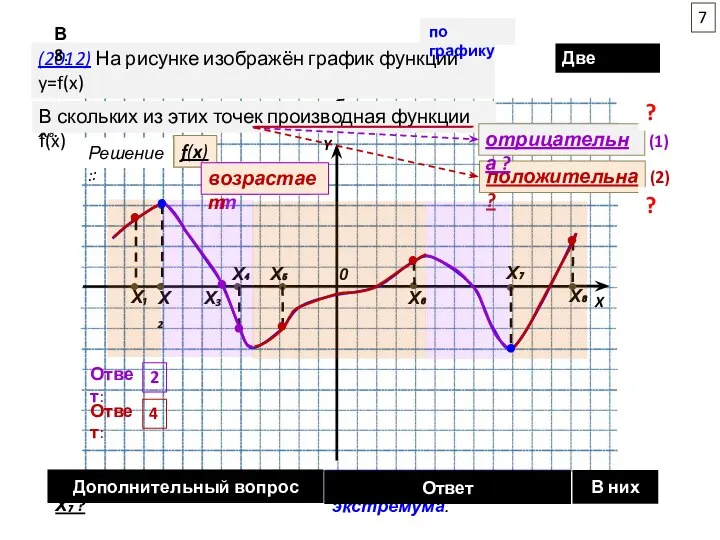
число точек, в которых
касательные к графику функции у=f(x)
параллельны прямой
а) у = -13
б) у = 2х+5
4
2
0
1
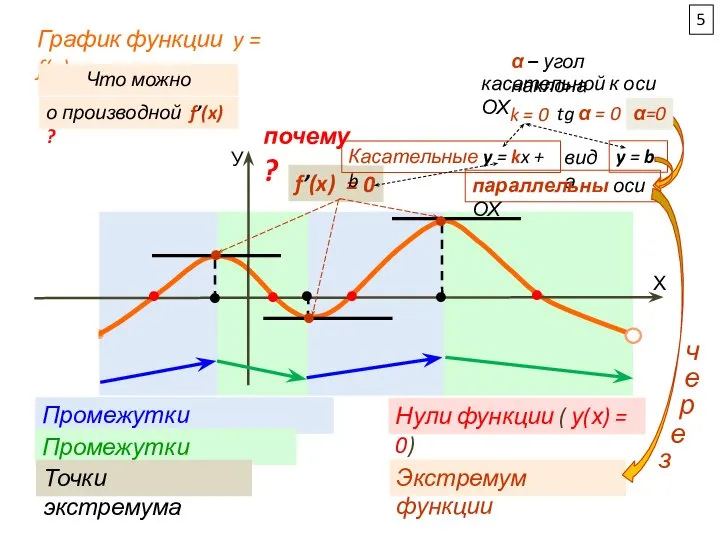
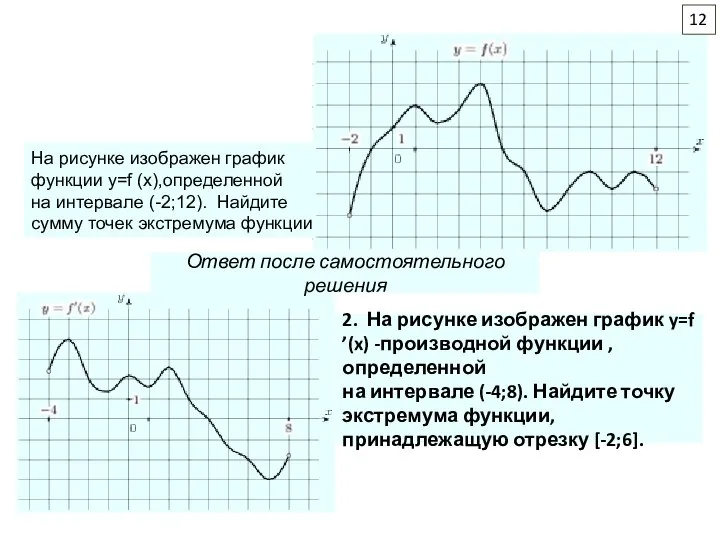
2. Найдите точку наибольшего значения функции f(x) на отрезке [5;9]
9
–8
15
/////////////////////
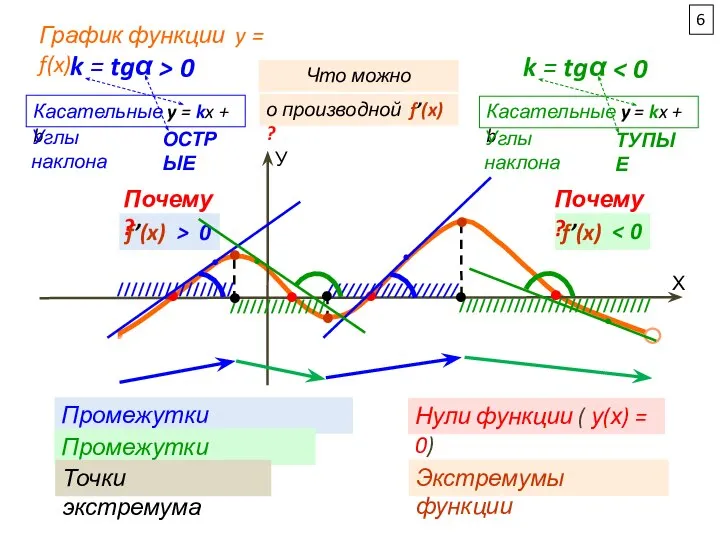
f’(x) > 0
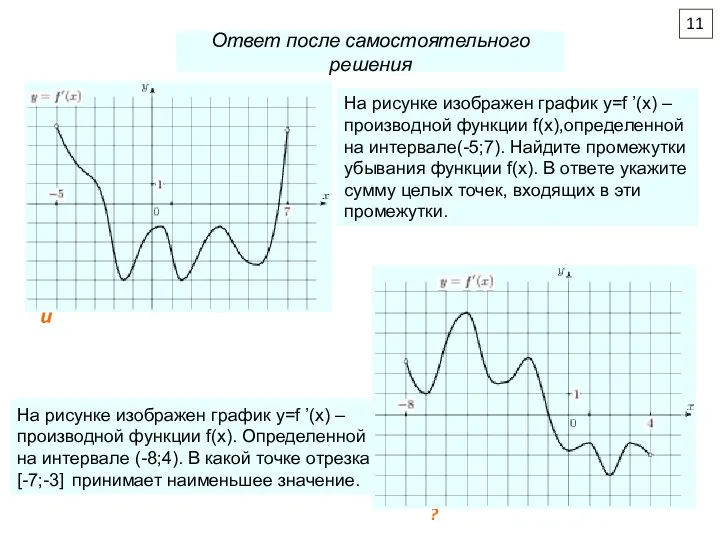
3. Укажите число промежутков убывания функции y = f(x)
3
1
•
•
•
•
К
Л
Ю
Ч
4. Укажите число целых точек, в которых функция y = f(x) возрастает
1
2
3
4
5
11
6
7
8
9
10
12
13
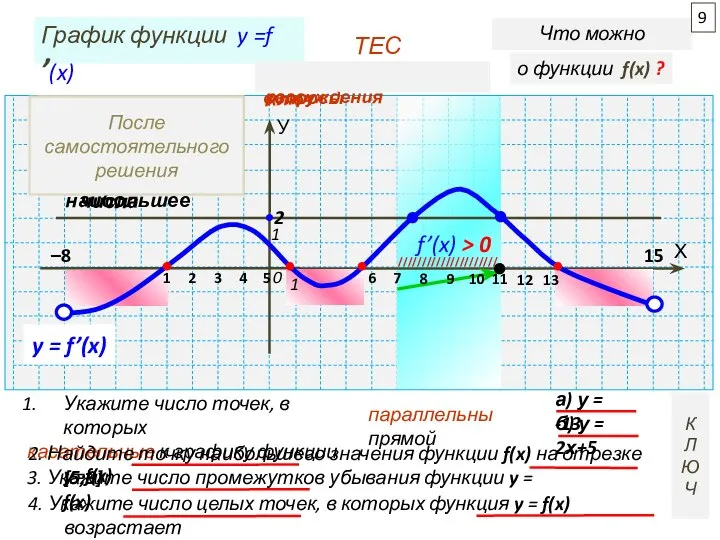
ТЕСТ
Ответить на все вопросы
проверить, кликнув ключ
сверить свои рассуждения
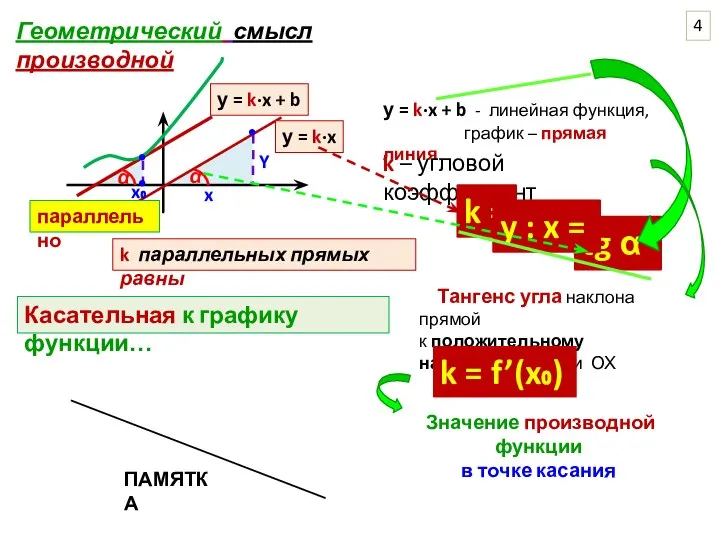
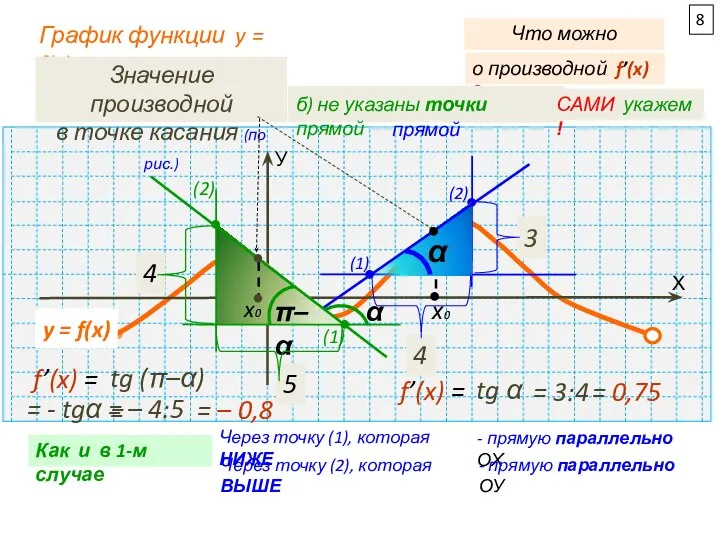
1а.
касательная y= kx+b
данная прямая y=0x-13
f’(x) = k = 0
1б.
Дана прямая у=2х+5
f’(x) = 2
k=2 у всех параллельных
прямых
•2
•
•
2.
График f’(x)
выше оси ОХ
f(x) - возрастает
•
f(9) - наибольшее
3.
f(X) - убывает -
на промежутках, где
f’(x) ≤ 0
4.
Это абсциссы точек
промежутков
возрастания (f’(x) ≥ 0)
целые числа
После
самостоятельного
решения
9

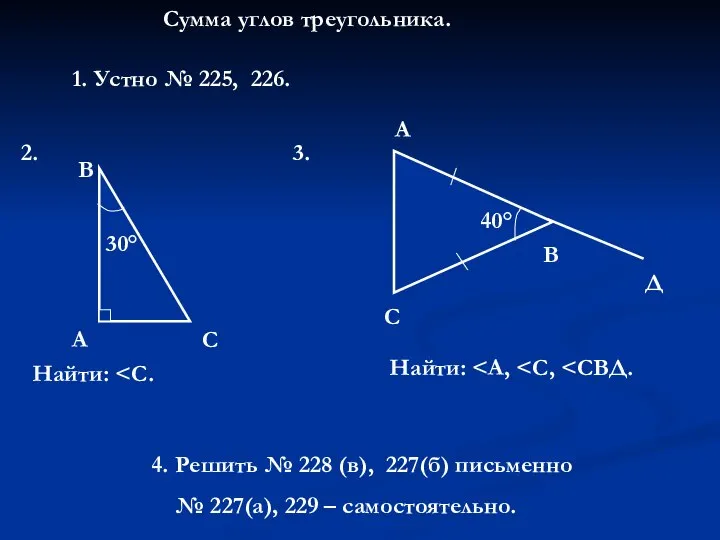 Сумма углов треугольника
Сумма углов треугольника Презентация на тему Знакомые и незнакомые единицы измерения площади
Презентация на тему Знакомые и незнакомые единицы измерения площади  Геометрические фигуры в жизни и в природе. Проект
Геометрические фигуры в жизни и в природе. Проект Определение синуса, косинуса и тангенса угла
Определение синуса, косинуса и тангенса угла Правильные многогранники
Правильные многогранники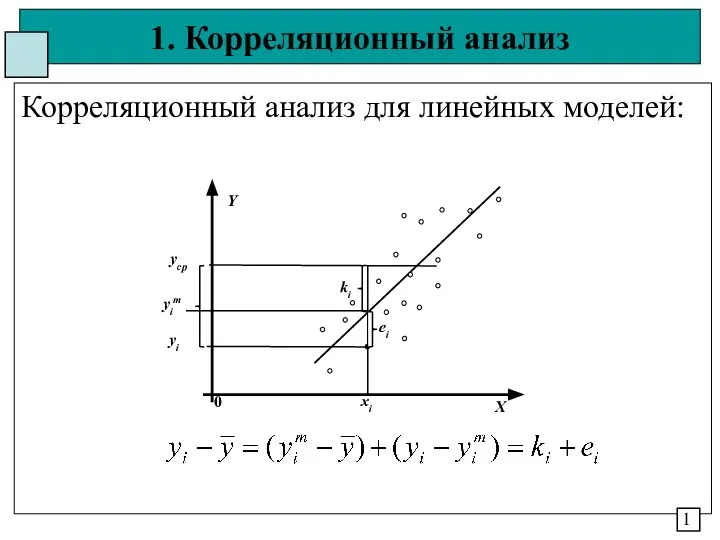 Корреляционный анализ для линейных моделей
Корреляционный анализ для линейных моделей Средняя линия треугольника
Средняя линия треугольника Знаки математических действий
Знаки математических действий Планы второго порядка
Планы второго порядка Виды треугольников. 3 класс
Виды треугольников. 3 класс Геометрические фигуры
Геометрические фигуры Изучение таблицы деления
Изучение таблицы деления Деление десятичных дробей. Решение уравнений
Деление десятичных дробей. Решение уравнений Контрольная работа №8 по теме Разложение многочленов на множители
Контрольная работа №8 по теме Разложение многочленов на множители Эндогенность. Инструментальные переменные
Эндогенность. Инструментальные переменные Осевая симметрия
Осевая симметрия Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница
Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница Графы. ЕГЭ задание 15. Урок 11 А
Графы. ЕГЭ задание 15. Урок 11 А Готовимся к ЕГЭ-2015 по математике. Решение 1 части реального теста ЕГЭ-2014
Готовимся к ЕГЭ-2015 по математике. Решение 1 части реального теста ЕГЭ-2014 Линейное уравнение с двумя переменными и его график. 7 класс
Линейное уравнение с двумя переменными и его график. 7 класс Презентация на тему Сложение многозначных чисел
Презентация на тему Сложение многозначных чисел  формулы
формулы Математика и режим дня
Математика и режим дня Таблица умножения и деления на 2
Таблица умножения и деления на 2 Математические ребусы
Математические ребусы Перпендикулярность в пространстве. Тест. Практическая часть
Перпендикулярность в пространстве. Тест. Практическая часть Задача на арифметическую прогрессию. 9 класс
Задача на арифметическую прогрессию. 9 класс Алгоритм умножения
Алгоритм умножения