Содержание
- 2. Векторная алгебра Определение Вектором называется направленный отрезок Обозначение вектора: - длина вектора Определение Вектор, длина которого
- 3. Векторная алгебра Определение Единичный вектор, направление которого совпадает с направлением вектора называется ортом вектора и обозначается
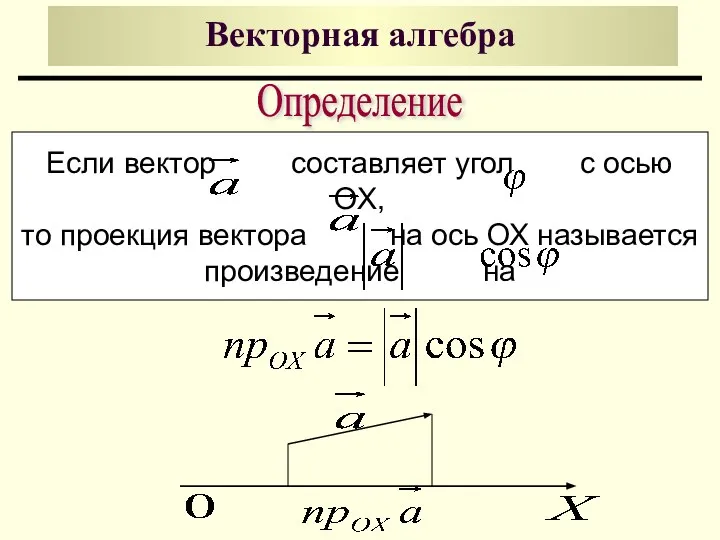
- 4. Векторная алгебра Если вектор составляет угол с осью OX, то проекция вектора на ось ОХ называется
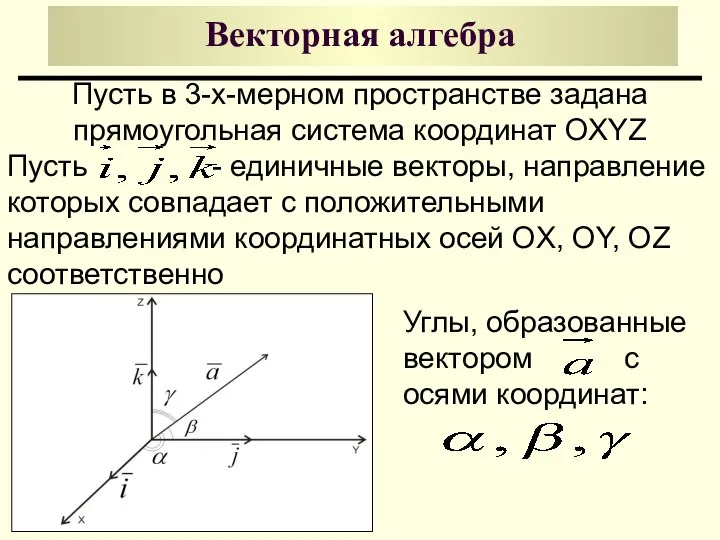
- 5. Векторная алгебра Пусть в 3-х-мерном пространстве задана прямоугольная система координат OXYZ Пусть - единичные векторы, направление
- 6. Векторная алгебра Проекция вектора на оси координат Вектор имеет координаты x, y, z, то есть в
- 7. Действия сложения векторов и умножения вектора на число называются линейными операциями над векторами Векторная алгебра Пусть
- 8. Векторы называются линейно зависимыми, если существуют такие действительные числа одновременно не обращающиеся в ноль , что
- 9. Пример Рассмотрим на плоскости два неколлинеарных вектора и Покажем, что эти векторы линейно независимы (метод от
- 10. Пример Проверим, являются ли линейно зависимыми вектора По определению линейно (не)зависимых векторов Запишем это равенство для
- 11. Пример Получена система линейных однородных уравнений относительно неизвестных . Если ранг матрицы системы меньше 3, то
- 12. Пример Вектора линейно независимые
- 13. Векторная алгебра Пусть - неколлинеарные векторы на плоскости, тогда всякий комплонарный им вектор можно представить и
- 14. Векторная алгебра Доказательство 1) Покажем существование разложения По условию векторы - неколлинеарные векторы эти векторы не
- 15. Векторная алгебра В случае, если тогда разложение (2) справедливо при Одновременное выполнение не может быть
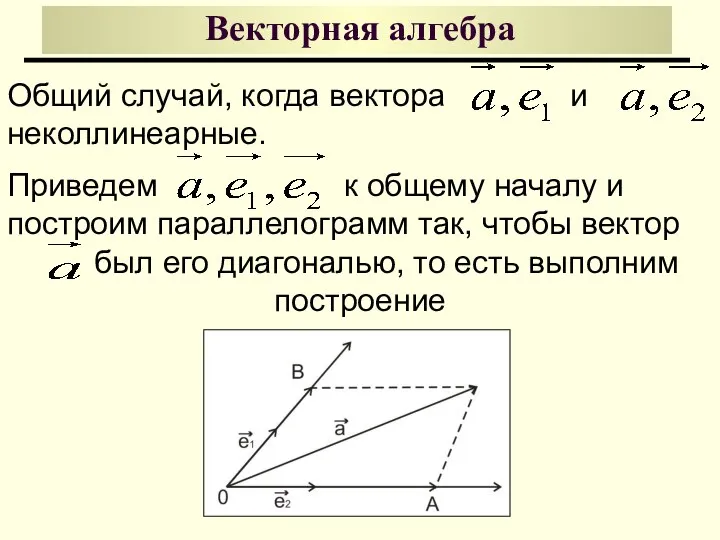
- 16. Векторная алгебра Общий случай, когда вектора и неколлинеарные. Приведем к общему началу и построим параллелограмм так,
- 17. Векторная алгебра По правилу сложению векторов Таким образом, разложение (2) существует
- 18. Векторная алгебра 1) Докажем единственность разложения (2) Предположим противное, что разложение (2) не единственно, то есть
- 19. Векторная алгебра Таким образом, существует такое число что выполняется (*) вектора . коллинеарные, что противоречит условию
- 21. Скачать презентацию















 Пропорции. Задачи
Пропорции. Задачи Презентация на тему Движение
Презентация на тему Движение  Сложение и вычитание числа 2
Сложение и вычитание числа 2 Математика
Математика Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ  Математика и спорт
Математика и спорт Разложение вектора по трём некомпланарным векторам
Разложение вектора по трём некомпланарным векторам Десятки, единицы, цифры
Десятки, единицы, цифры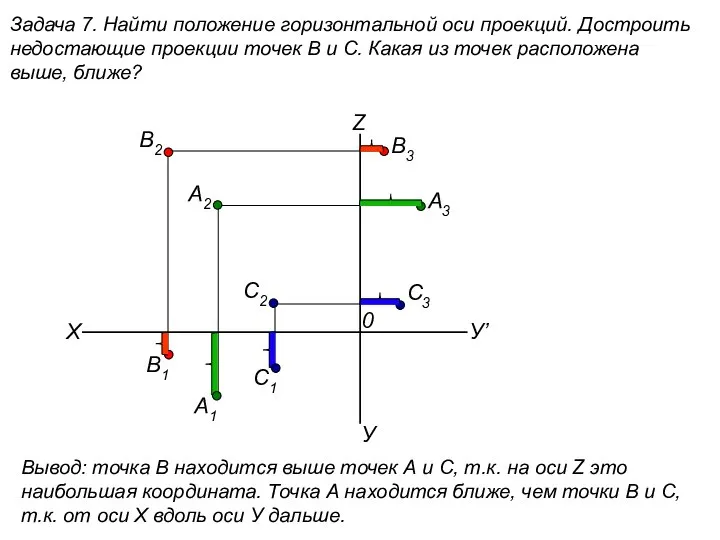 Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7)
Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7) Уравнение касательной к графику функции
Уравнение касательной к графику функции Решение уравнений. Первый и второй уровни
Решение уравнений. Первый и второй уровни Предельные величины, эластичности
Предельные величины, эластичности Математика – наука о наиболее общих и фундаментальных структурах реального мира
Математика – наука о наиболее общих и фундаментальных структурах реального мира Практическое применение треугольников в жизни
Практическое применение треугольников в жизни Освоение основных универсальных предметных знаний и умений в курсе технологии
Освоение основных универсальных предметных знаний и умений в курсе технологии Ряды динамики
Ряды динамики Презентация по математике "Знакомство с занимательной литературой по математике" -
Презентация по математике "Знакомство с занимательной литературой по математике" -  Простейшие функции и их графики
Простейшие функции и их графики Решение тригонометрических уравнений
Решение тригонометрических уравнений Логарифмические уравнения
Логарифмические уравнения Занимательные задачи
Занимательные задачи Комбинаторика
Комбинаторика Площадь параллелограмма. 8 класс
Площадь параллелограмма. 8 класс Соста числа 11
Соста числа 11 Обратные тригонометрические функции
Обратные тригонометрические функции Десятичный и натуральный логарифм
Десятичный и натуральный логарифм Параллельный перенос
Параллельный перенос Геймификация образовательного процесса на уроках математики с использованием двигательной активности
Геймификация образовательного процесса на уроках математики с использованием двигательной активности