Основные распределения математической статистики

Содержание
НУУз. каф ТВиМС. проф. Г.М.Раимова
1. Нормальное распределение.

Основные распределения МС
Основные распределения, используемые в математической статистике:
нормальное распределение,
распределение хи- квадрат,
распределения Стьюдента
распределение Фишера.
При статических исследованиях широко используются случайные величины, имеющие нормальное распределение, распределение χ2 (хи- квадрат), распределения Стьюдента и Фишера.
НУУз. каф ТВиМС. проф. Г.М.Раимова

Нормальное распределение
Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний.
Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех.
Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
НУУз. каф ТВиМС. проф. Г.М.Раимова

Нормальное распределение, также называемое распределением Гаусса или Гаусса—Лапласа —распределение вероятностей, которое задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:
где параметр μ — математическое ожидание (среднее значение), медиана и мода распределения, а параметр σ— среднеквадратическое отклонение (σ2 —дисперсия) распределения.
НУУз. каф ТВиМС. проф. Г.М.Раимова
Нормальное распределение –N(μ,σ2)

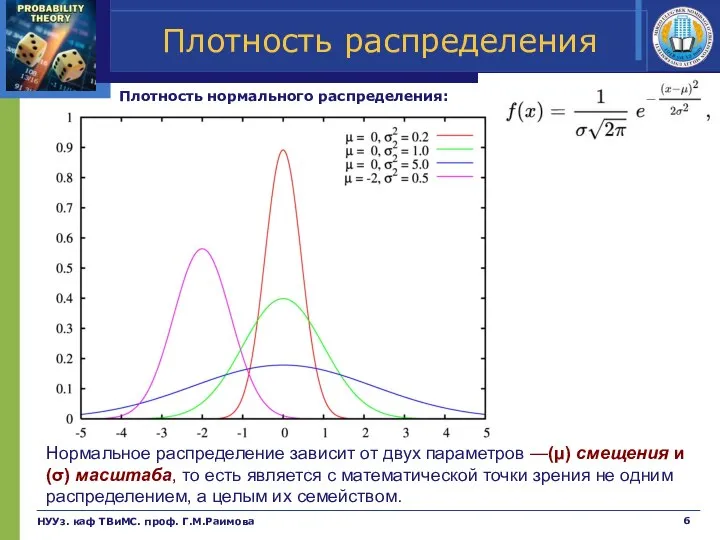
Плотность нормального распределения:
НУУз. каф ТВиМС. проф. Г.М.Раимова
Плотность распределения
Нормальное распределение зависит от двух параметров —(μ) смещения и (σ) масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством.

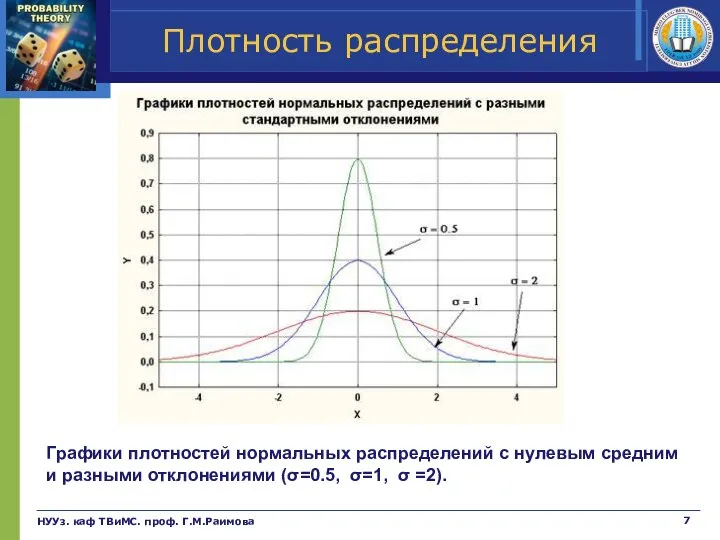
НУУз. каф ТВиМС. проф. Г.М.Раимова
Плотность распределения
Графики плотностей нормальных распределений c нулевым средним и разными отклонениями (σ=0.5, σ=1, σ =2).

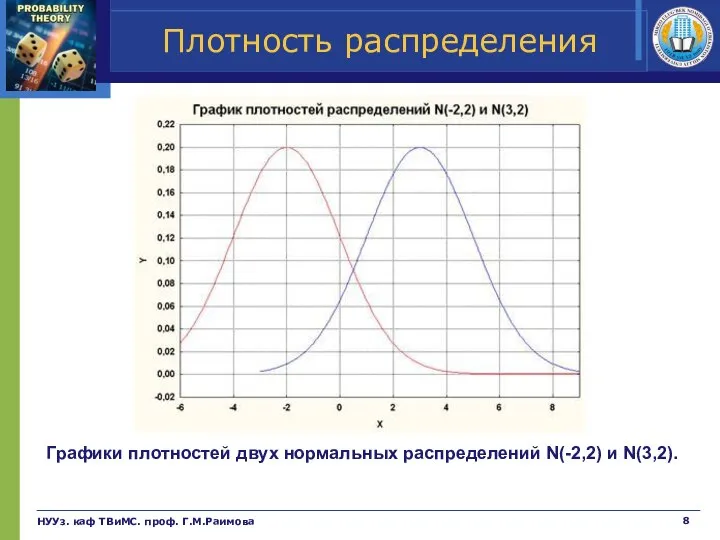
НУУз. каф ТВиМС. проф. Г.М.Раимова
Плотность распределения
Графики плотностей двух нормальных распределений N(-2,2) и N(3,2).

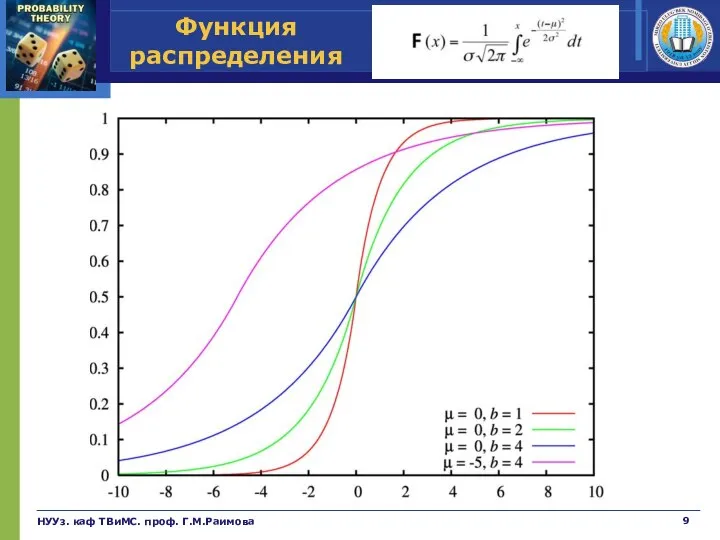
Функция распределения
НУУз. каф ТВиМС. проф. Г.М.Раимова

Нормальное распределение
НУУз. каф ТВиМС. проф. Г.М.Раимова

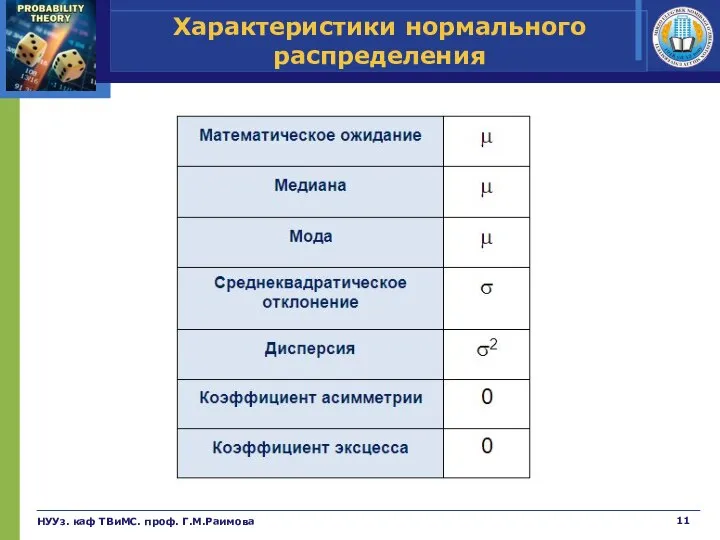
Характеристики нормального распределения
НУУз. каф ТВиМС. проф. Г.М.Раимова

Моменты
Если Х имеет нормальное распределение, то для неё существуют (конечные) моменты при всех p с действительной частью больше −1.
Для неотрицательных целых p, центральные моменты таковы:
Центральные абсолютные моменты для неотрицательных целых p таковы:
НУУз. каф ТВиМС. проф. Г.М.Раимова

Правило сигм
Нормально распределенная случайная величина с большой вероятностью принимает значения, близкие к своему математическому ожиданию, что выражается правилом сигм:
Чаще всего используется правило трех сигм, т.е. k = 3.
НУУз. каф ТВиМС. проф. Г.М.Раимова

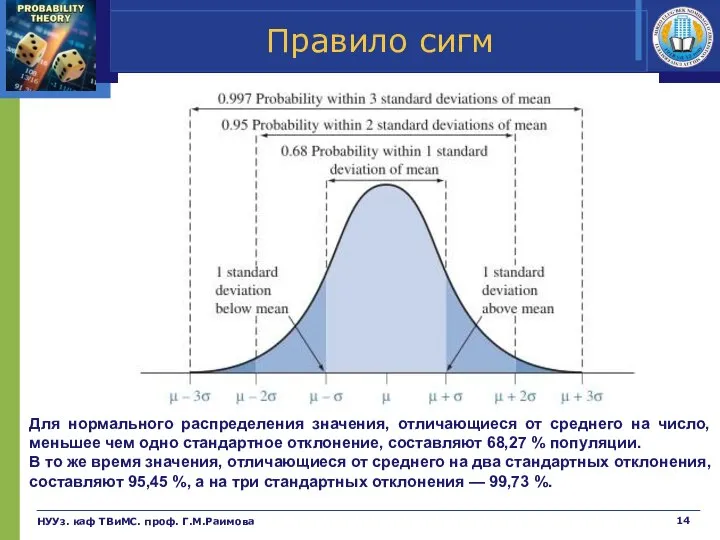
Правило сигм
НУУз. каф ТВиМС. проф. Г.М.Раимова
Для нормального распределения значения, отличающиеся от среднего на число, меньшее чем одно стандартное отклонение, составляют 68,27 % популяции.
В то же время значения, отличающиеся от среднего на два стандартных отклонения, составляют 95,45 %, а на три стандартных отклонения — 99,73 %.

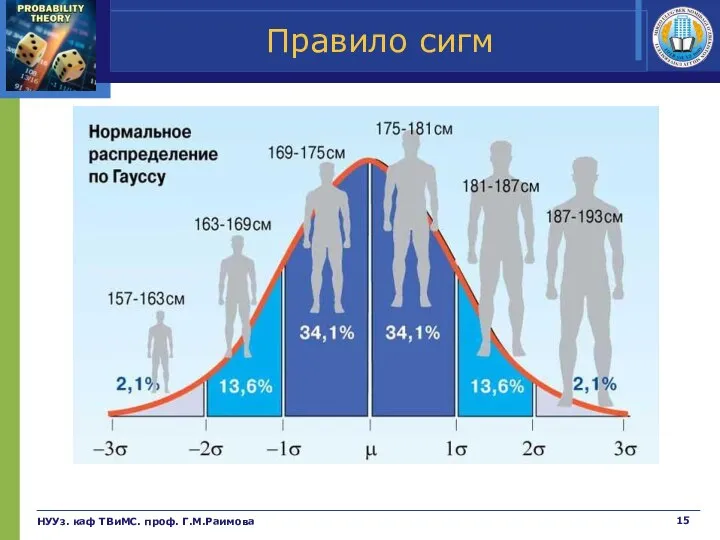
Правило сигм
НУУз. каф ТВиМС. проф. Г.М.Раимова

Стандартное нормальное распределение - N(0,1)
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.
НУУз. каф ТВиМС. проф. Г.М.Раимова

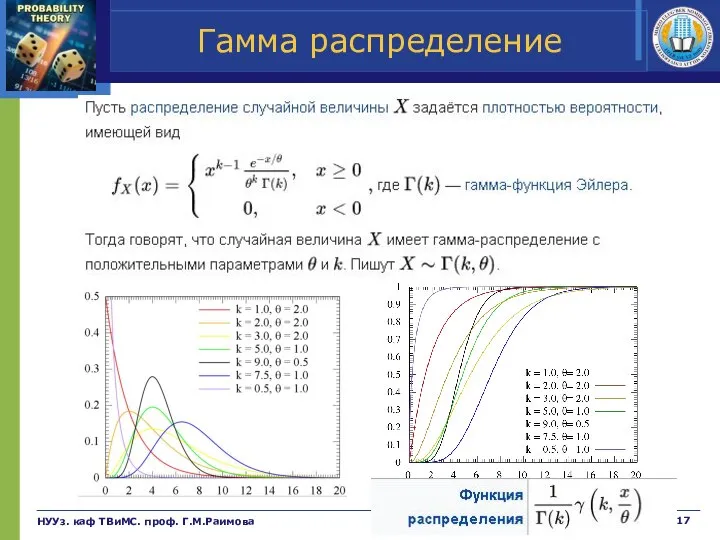
Гамма распределение
НУУз. каф ТВиМС. проф. Г.М.Раимова

Хи-квадрат распределение
Пусть ξ1,…, ξk — совместно независимые стандартные нормальные случайные величины, то есть: ξi ~N(0,1).
Тогда случайная величина
имеет распределение хи-квадрат с k степенями свободы, то есть
НУУз. каф ТВиМС. проф. Г.М.Раимова

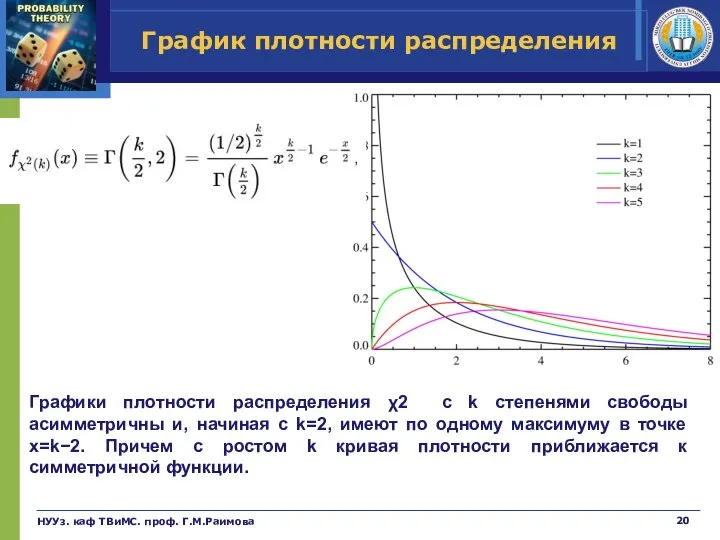
Распределение хи-квадрат
Распределение хи-квадрат является частным случаем гамма распределения, и его плотность имеет вид:
где Г(k/2,2) означает гамма-распределение, а Г(k/2) — гамма функции.
НУУз. каф ТВиМС. проф. Г.М.Раимова

График плотности распределения
НУУз. каф ТВиМС. проф. Г.М.Раимова
Графики плотности распределения χ2 с k степенями свободы асимметричны и, начиная с k=2, имеют по одному максимуму в точке x=k−2. Причем с ростом k кривая плотности приближается к симметричной функции.

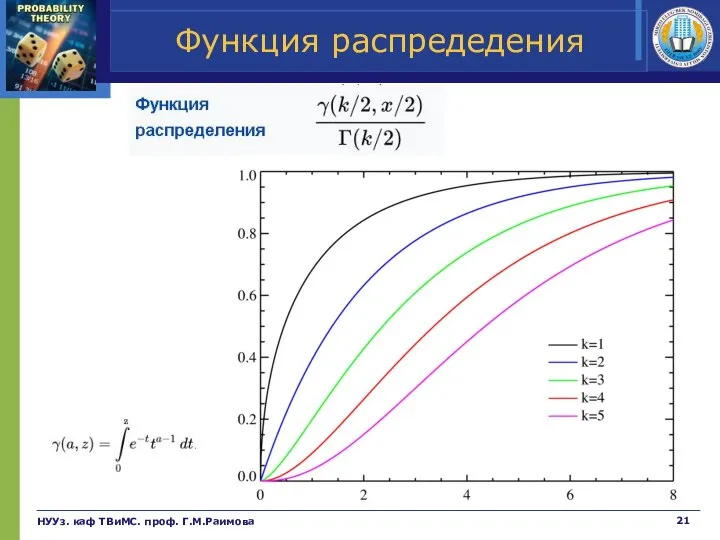
Функция распредедения
НУУз. каф ТВиМС. проф. Г.М.Раимова

Характеристики распределения
НУУз. каф ТВиМС. проф. Г.М.Раимова

Распределение Стьюдента
Распределение Стьюдента (t-распределение) в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений.
Уильям Сили Госсет первым опубликовал работы, посвящённые этому распределению, под псевдонимом «Стьюдент».
НУУз. каф ТВиМС. проф. Г.М.Раимова

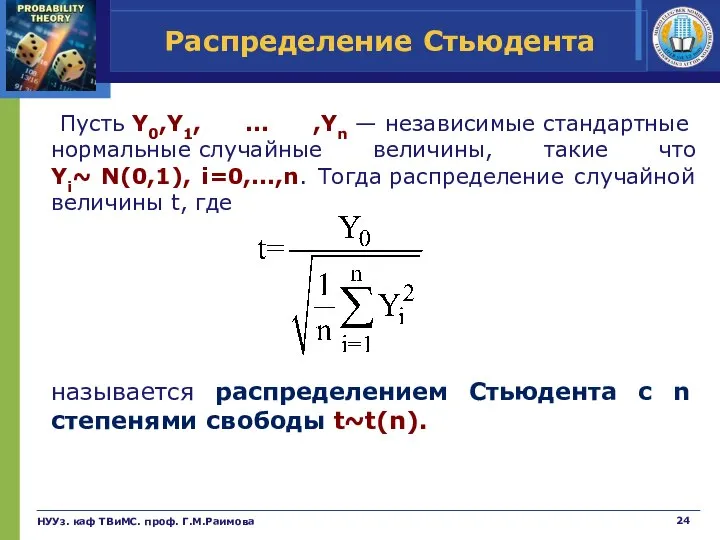
Распределение Стьюдента
Пусть Y0,Y1, ... ,Yn — независимые стандартные нормальные случайные величины, такие что Yi~ N(0,1), i=0,...,n. Тогда распределение случайной величины t, где
называется распределением Стьюдента с n степенями свободы t~t(n).
НУУз. каф ТВиМС. проф. Г.М.Раимова

Распределение Стьюдента
Пусть случайная величина Y имеет распределение N(0,1), а независимая от Y случайная величина Z принадлежит χ2(n) (имеет распределение χ2 c n степенями свободы).
Тогда случайная величина
имеет распределение Стьюдента с n степенями свободы (t(n) - распределение)
НУУз. каф ТВиМС. проф. Г.М.Раимова

Плотность распределения
НУУз. каф ТВиМС. проф. Г.М.Раимова

Плотность распределения
НУУз. каф ТВиМС. проф. Г.М.Раимова
Также плотность распределения Стьюдента можно выразить воспользовавшись бета-функцией Эйлера B:
Бета-функцией (B-функцией, бета-функцией Эйлера или интегралом Эйлера I рода) называется следующая функция от двух переменных:

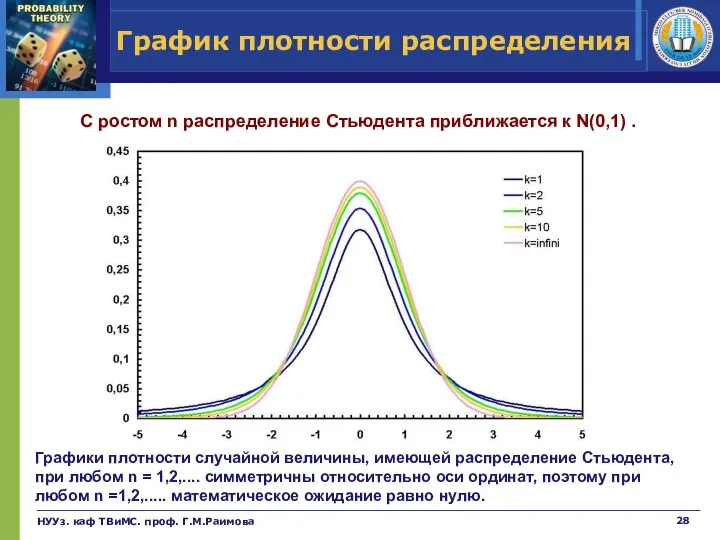
НУУз. каф ТВиМС. проф. Г.М.Раимова
График плотности распределения
Графики плотности случайной величины, имеющей распределение Стьюдента, при любом n = 1,2,.... симметричны относительно оси ординат, поэтому при любом n =1,2,..... математическое ожидание равно нулю.
С ростом n распределение Стьюдента приближается к N(0,1) .

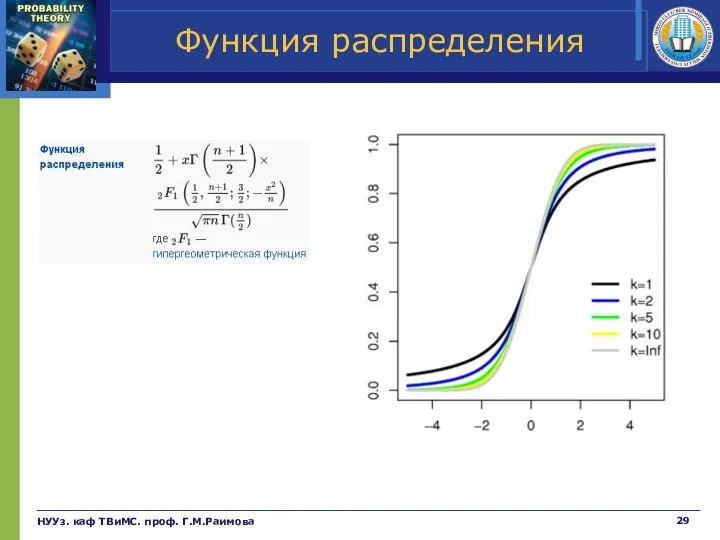
Функция распределения
НУУз. каф ТВиМС. проф. Г.М.Раимова

Характеристики распределения
НУУз. каф ТВиМС. проф. Г.М.Раимова

Распределение Фишера
НУУз. каф ТВиМС. проф. Г.М.Раимова

Плотность распределения
НУУз. каф ТВиМС. проф. Г.М.Раимова
Плотностьраспределения Х~F(n1;n2)

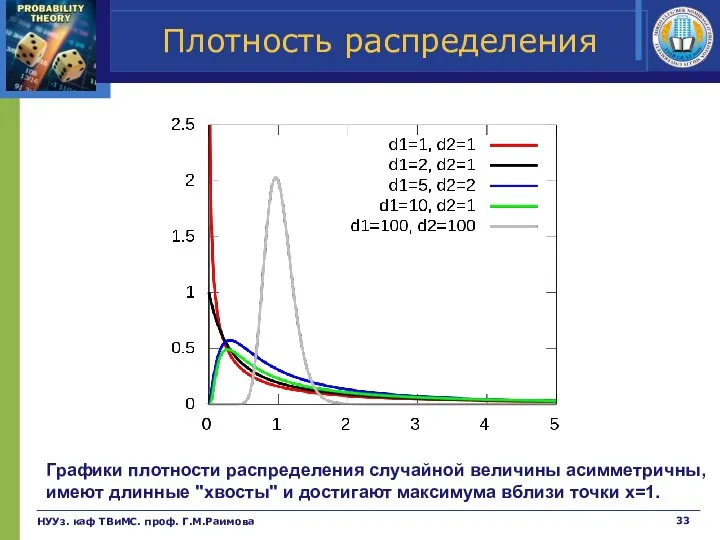
Плотность распределения
НУУз. каф ТВиМС. проф. Г.М.Раимова
Графики плотности распределения случайной величины асимметричны, имеют длинные "хвосты" и достигают максимума вблизи точки x=1.

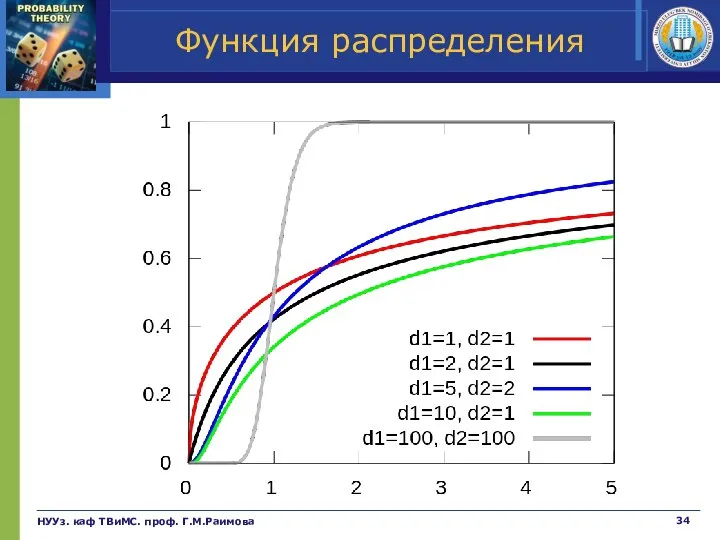
Функция распределения
НУУз. каф ТВиМС. проф. Г.М.Раимова

Характеристики распределения
НУУз. каф ТВиМС. проф. Г.М.Раимова