Содержание
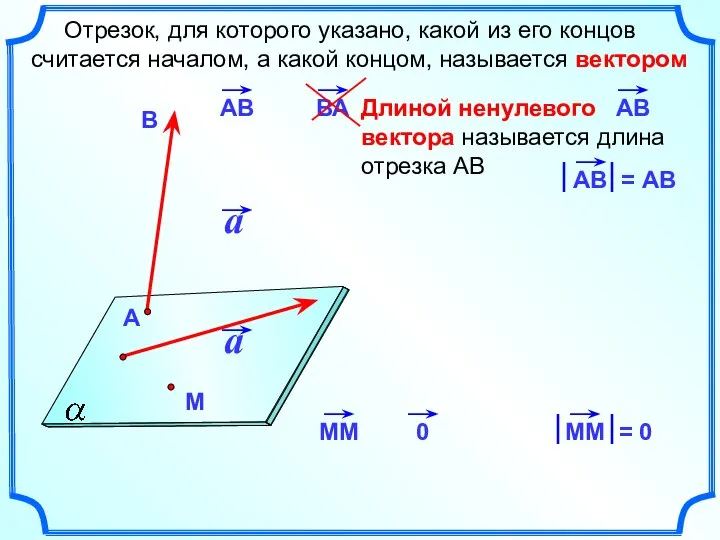
- 2. Отрезок, для которого указано, какой из его концов считается началом, а какой концом, называется вектором
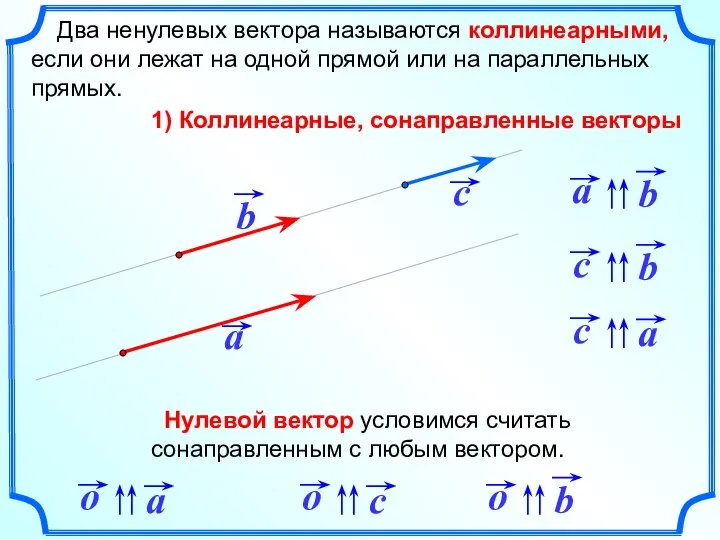
- 3. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. 1)
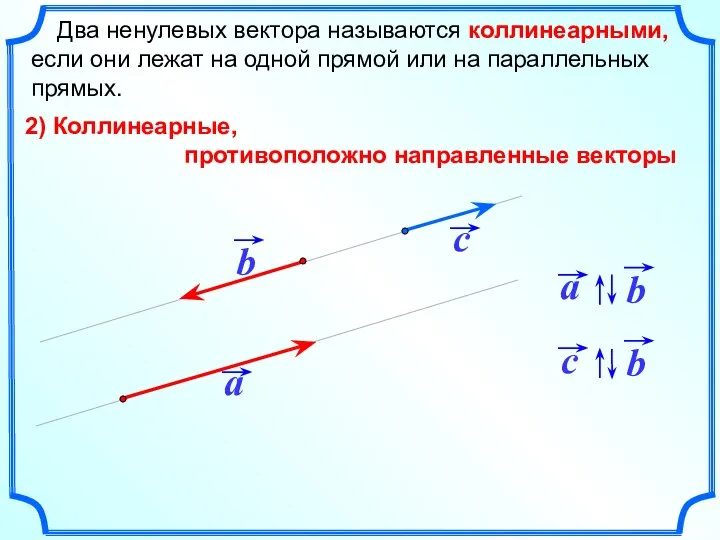
- 4. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. 2)
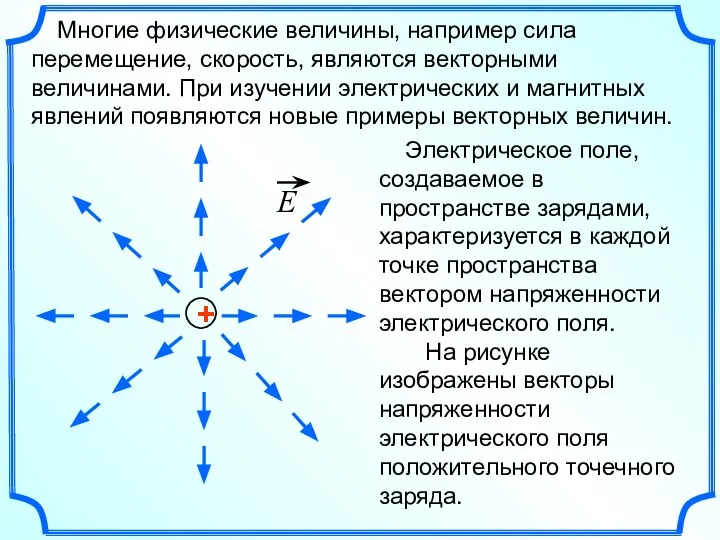
- 5. Многие физические величины, например сила перемещение, скорость, являются векторными величинами. При изучении электрических и магнитных явлений
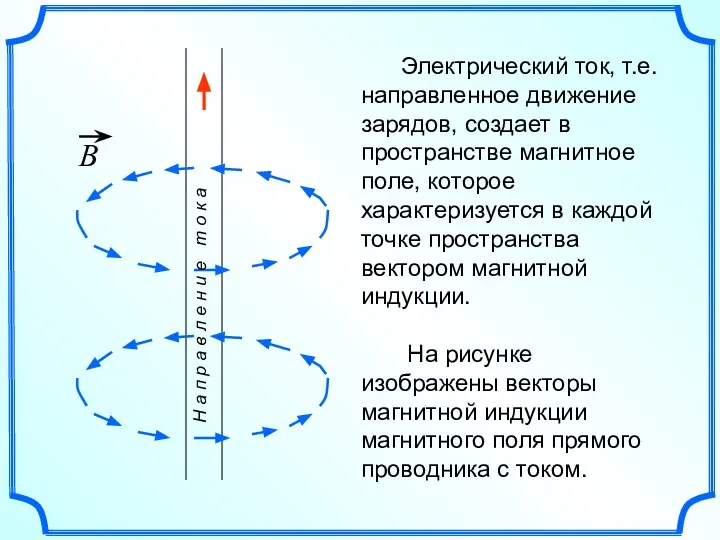
- 6. Электрический ток, т.е. направленное движение зарядов, создает в пространстве магнитное поле, которое характеризуется в каждой точке
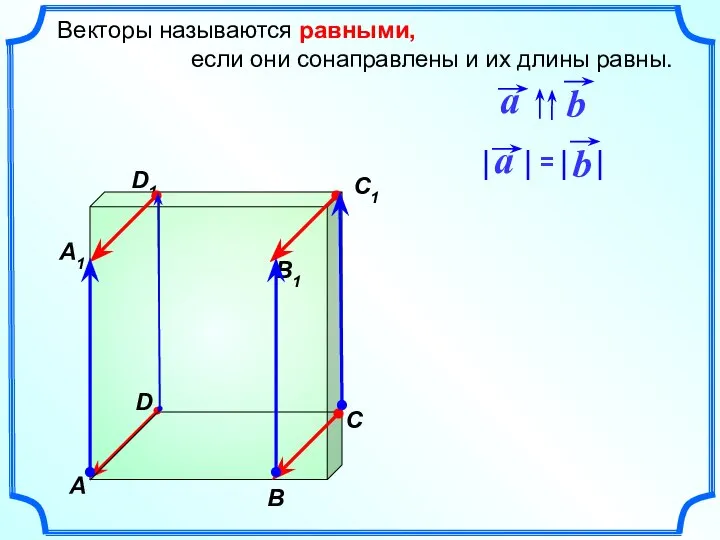
- 7. Векторы называются равными, если они сонаправлены и их длины равны.
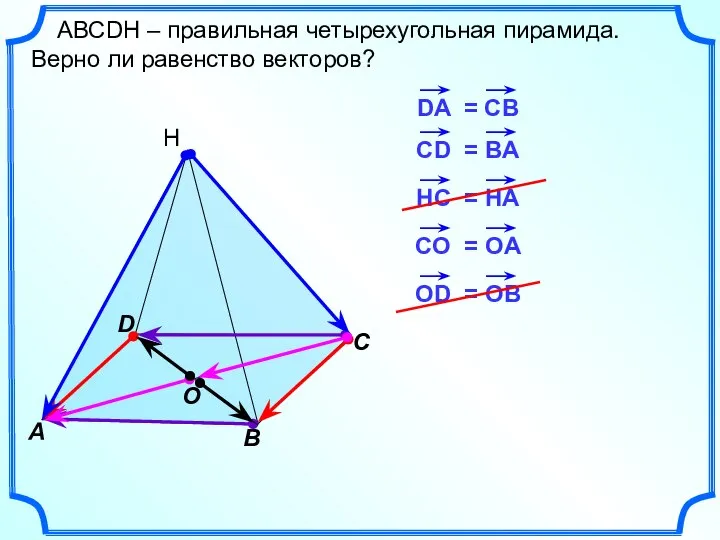
- 8. D А АВСDH – правильная четырехугольная пирамида. Верно ли равенство векторов? Н В С O
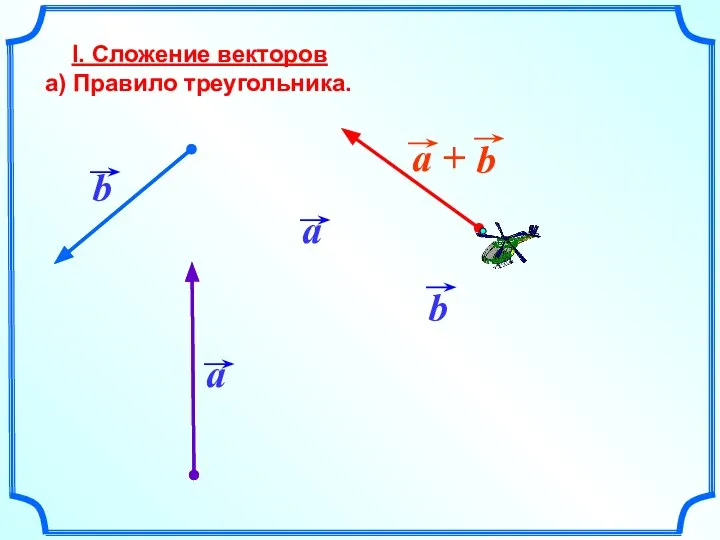
- 9. I. Сложение векторов а) Правило треугольника. b
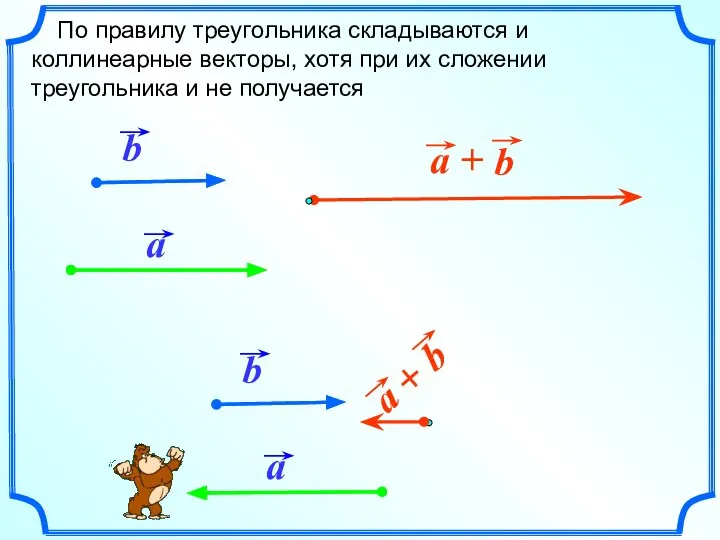
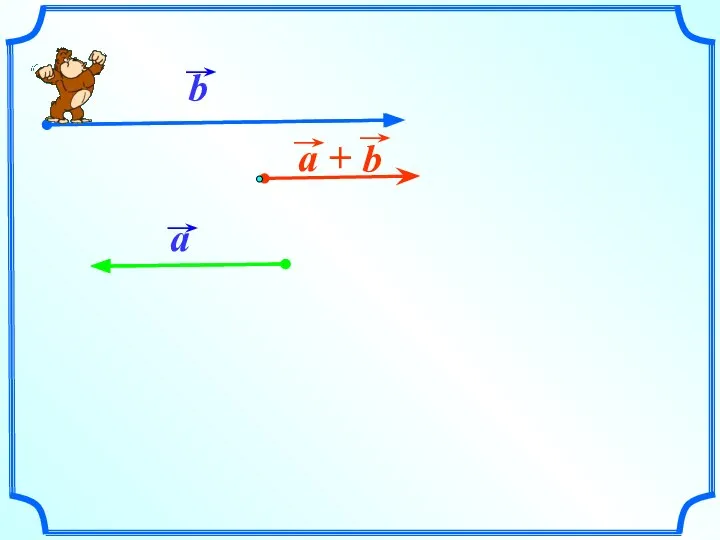
- 10. По правилу треугольника складываются и коллинеарные векторы, хотя при их сложении треугольника и не получается
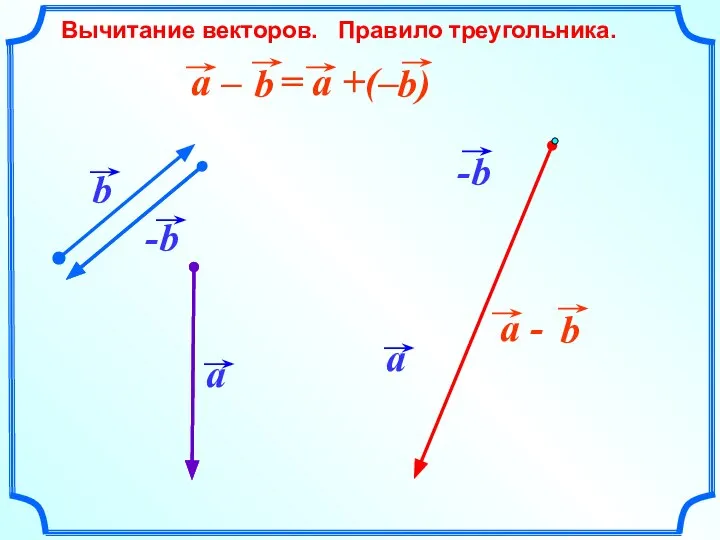
- 12. Вычитание векторов. Правило треугольника.
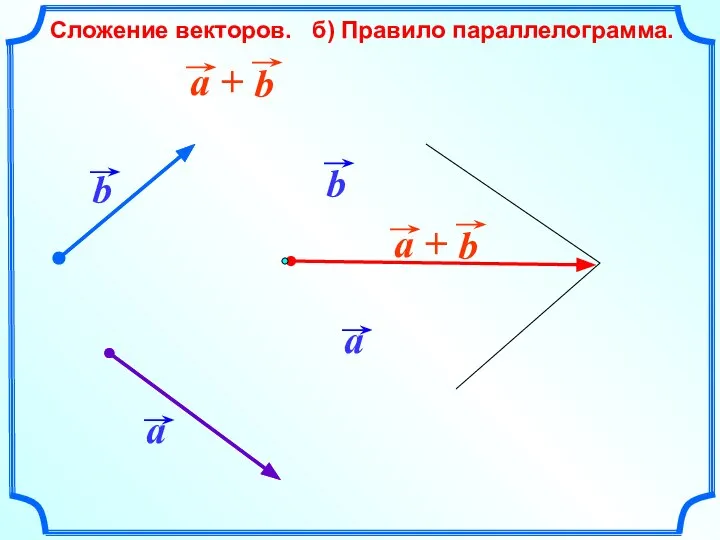
- 13. Сложение векторов. б) Правило параллелограмма.
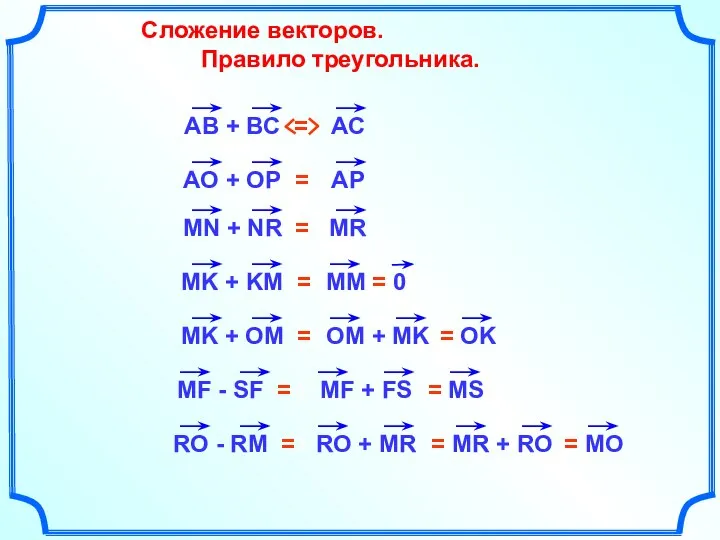
- 14. Сложение векторов. Правило треугольника.
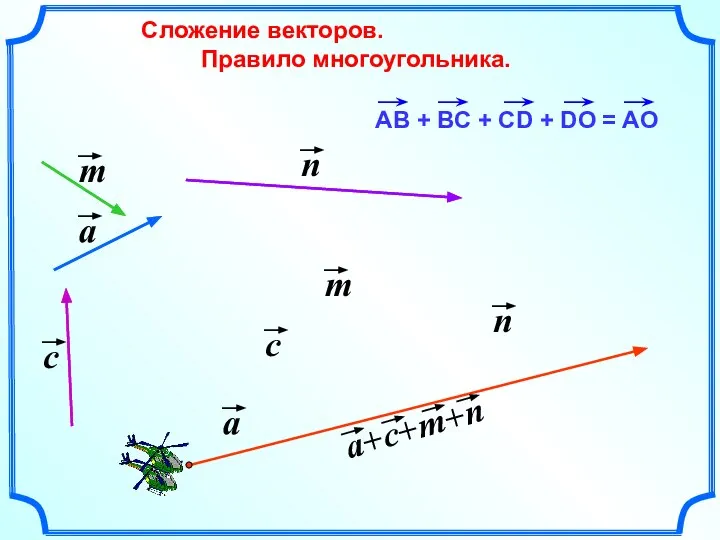
- 15. Сложение векторов. Правило многоугольника.
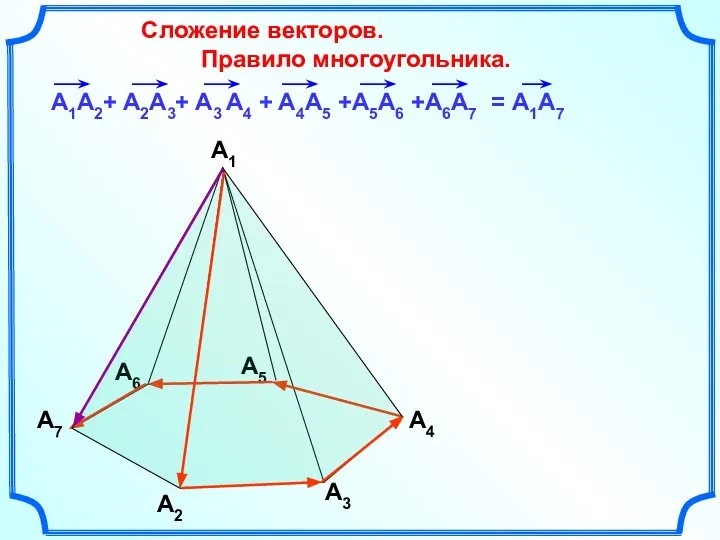
- 16. Сложение векторов. Правило многоугольника. A1 A2 A3 A4 A5 A6 A7
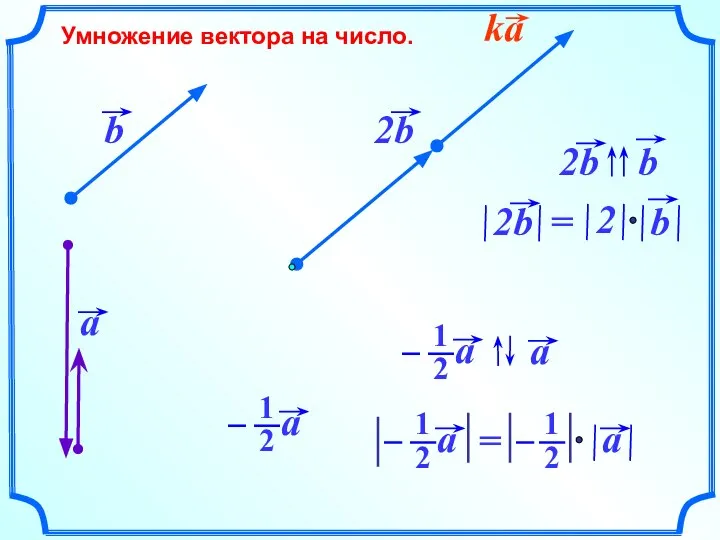
- 17. Умножение вектора на число.
- 19. Скачать презентацию
 Ломаная линия
Ломаная линия двугранный угол. перпендикулярные плоскости. признак
двугранный угол. перпендикулярные плоскости. признак Способы решения тригонометрических уравнений
Способы решения тригонометрических уравнений Пирамида
Пирамида Найдите производную функции. Практическая работа
Найдите производную функции. Практическая работа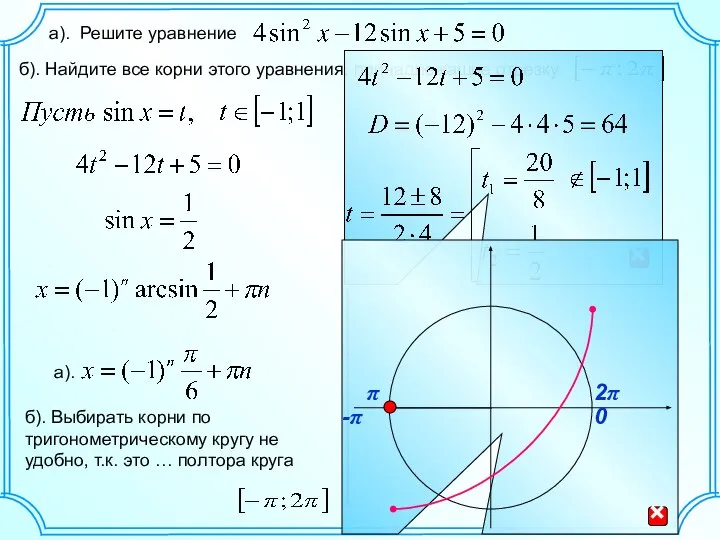 Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Пересечение поверхностей геометрических тел. Комплексный чертеж усеченного гранного тела, развертка поверхности
Пересечение поверхностей геометрических тел. Комплексный чертеж усеченного гранного тела, развертка поверхности Геометрические преобразования графиков функций
Геометрические преобразования графиков функций Теория вероятностей. Случайные события
Теория вероятностей. Случайные события Многогранники в нашей жизни
Многогранники в нашей жизни Решение задач. Многогранники. Тела вращения
Решение задач. Многогранники. Тела вращения Дифференциальные уравнения I порядка с разделяющимися переменными
Дифференциальные уравнения I порядка с разделяющимися переменными Вычитание вида 13
Вычитание вида 13 Решите систему неравенств и укажите все целые числа, которые являются ее решениями
Решите систему неравенств и укажите все целые числа, которые являются ее решениями Делители числа
Делители числа Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики Признаки параллельности прямых
Признаки параллельности прямых Квадратный корень и его свойства
Квадратный корень и его свойства Старинные русские меры длины
Старинные русские меры длины Цифровая азбука
Цифровая азбука Треугольник. Виды треугольников
Треугольник. Виды треугольников Уравнения и неравенства. Решение квадратных неравенств с помощью метода интервалов
Уравнения и неравенства. Решение квадратных неравенств с помощью метода интервалов Кривая Лоренца. Решение задач
Кривая Лоренца. Решение задач Корреляция. Причинность. Детерминизм
Корреляция. Причинность. Детерминизм Величина угла. Измерение углов. 5 класс
Величина угла. Измерение углов. 5 класс Квадрат и куб. 4 класс
Квадрат и куб. 4 класс Как можно заменить произведение равных сомножителей?
Как можно заменить произведение равных сомножителей? Тест Вписанные и описанные цилиндры
Тест Вписанные и описанные цилиндры