Задачи по комбинаторике

Цель нашего урока
целеполагание
Правило умножения очень полезно при решении многих комбинаторных
задач, однако его нельзя применять механически, не задумываясь
над смыслом и вопросом задачи.

Что сделано дома
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
?
б) 101∙100 = 10100;
?
б) 9∙8∙7∙6 = 3024;
?
9∙10∙10∙10∙5 = 45000;
9∙10∙10∙10∙2 = 18000;

Математическая разминка
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
Сколько будет всевозможных двузначных чисел из указанных цифр: 0, 3, 4, используя в записи числа каждую из них не более одного раза?
Сколько будет всевозможных двузначных чисел из указанных цифр: 1, 2, 3, если в записи числа допускается повторение цифр?

Задачи по комбинаторике
Организация и самоорганизация учащихся. Организация обратной связи
В турнире участвовало 16 шахматистов, причём
каждый с каждым сыграл по одной партии. Сколько всего было
сыграно партий?
Пример 2
Рассуждая, как в предыдущих примерах, можно подумать, что всего было сыграно 16 • 15 = 240 партий.

Анализируем
Практикум
(40∙39):2 = 780.
?
(50∙49):2 = 1225.
?

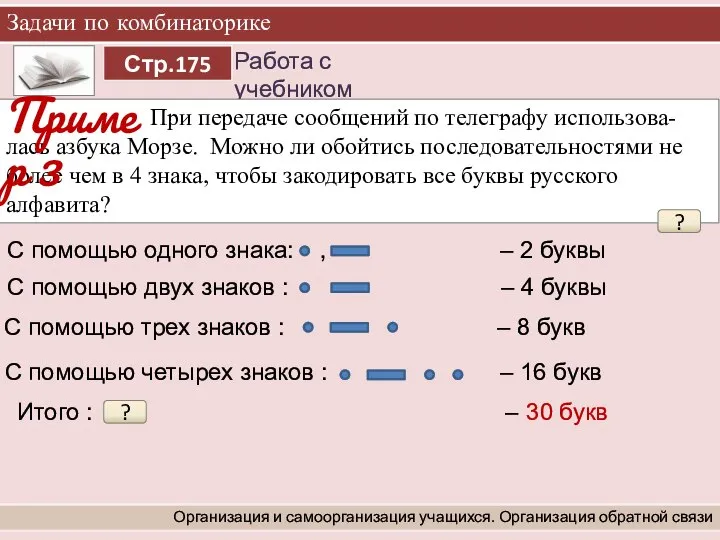
Итого : – 30 букв
Задачи по комбинаторике
Организация и самоорганизация учащихся. Организация обратной связи
При передаче сообщений по телеграфу использова-лась азбука Морзе. Можно ли обойтись последовательностями не более чем в 4 знака, чтобы закодировать все буквы русского
алфавита?
Пример 3
?
?

Анализируем и рассуждаем (продвинутым)
Практикум
25 = 32.
?
28 = 256.
?

Отрабатываем алгоритмы
Практикум
5
?
4
10

Отрабатываем алгоритмы
Практикум
5
?
2
5

Решение комбинаторных задач
Проверка полученных результатов. Коррекция

Решение комбинаторных задач (продвинутым)
Проверка полученных результатов. Коррекция

Вопросы и задания
Подведение итогов, рефлексия, домашнее задание.
1. Каким будет ответ задачи из примера 1, если:
а) первой цифрой кода не может быть 0;
б) код должен оканчиваться цифрой 5 или б;
в) первая цифра кода чётная, а вторая - нечётная?

Вопросы и задания
Подведение итогов, рефлексия, домашнее задание.
2. Какие из данных ниже задач аналогичны той, что описана в примере 2?
а) В спартакиаде приняли участие 7 боксёров, причём каждый с каждым провёл по одному бою. Сколько всего боёв было проведено?
б) На деловую встречу пришли 6 бизнесменов, и каждый с каждым обменялись рукопожатием. Сколько всего было сделано рукопожатий?
в) Четыре подруги каждая с каждой обменялись sms-сообщениями. Сколько всего было отправлено сообщений?
г) Пять государств установили друг с другом дипломатические отношения, при этом каждое с каждым обменялось послами. Сколько всего послов было направлено?
д) Четыре точки, никакие три из которых не лежат на одной прямой, соединили попарно отрезками. Сколько всего отрезков было проведено?