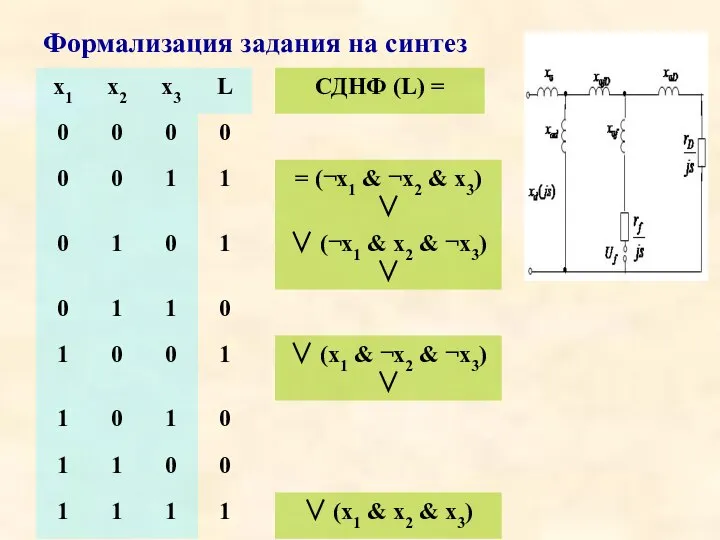
Слайд 2Из § 3.2: Свойства логических операций ∨, &, ¬ («Исходные соотношения»)

Слайд 72) Полезные соотношения для булевских формул

Слайд 8Доказательство - на примере (3.3.1а)

Слайд 10* Порядок замены – возможны варианты

Слайд 12Удалили повторяющиеся подформулы и переменные

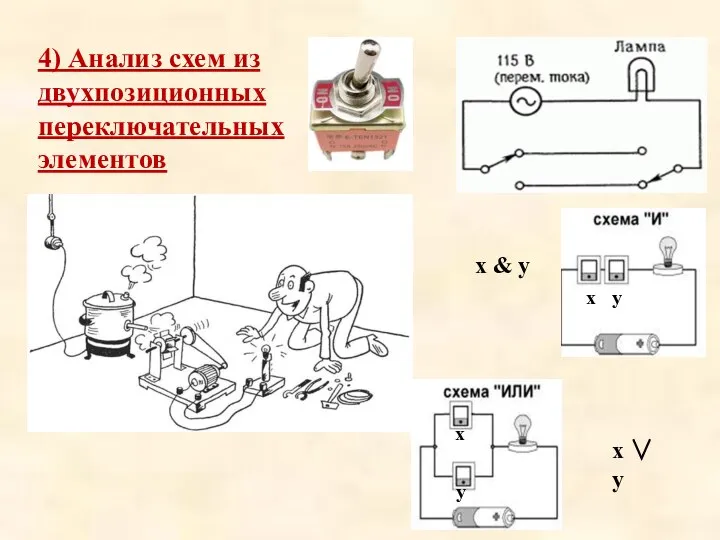
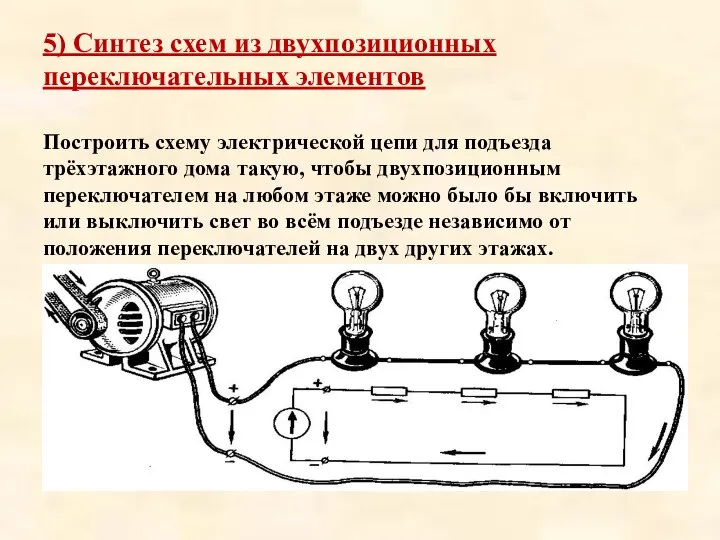
Слайд 294) Анализ схем из двухпозиционных переключательных элементов
x
y
x & y
x
y
x ∨ y
Слайд 30((x & y) ∨ ¬x ∨ (x & ¬y)) & ( (¬x

& y) ∨ ¬x) & x =
= (¬x ∨ y ∨ (x & ¬y)) & (¬x & x) =
= (¬x ∨ y ∨ x) & (¬x & x) =
= 1 & (¬x & x) = ¬x & x = 0
Слайд 31¬x & ((¬x & ¬y) ∨ (x & ¬y) ∨ ¬x) &

y =
= ¬x & ((¬x & ¬y) ∨ ¬x ∨ ¬y) & y =
= ¬x & (¬x ∨ ¬y) & y =
= (¬x & (¬x & y)) ∨ (¬x & ¬y & y) =
= (¬x & y) ∨ 0 = ¬x & y
Слайд 33Интересный другой вариант той же задачи:
Составить схему, позволяющую включать и выключать свет

в вашей комнате любым из трёх различных выключателей. Выключатели расположены у входа в комнату, над постелью и у письменного стола
(Медведева Я.С. Применение булевых функций к релейно-контактным схемам // Молодой учёный. — 2016. — № 3. — С. 8-11)
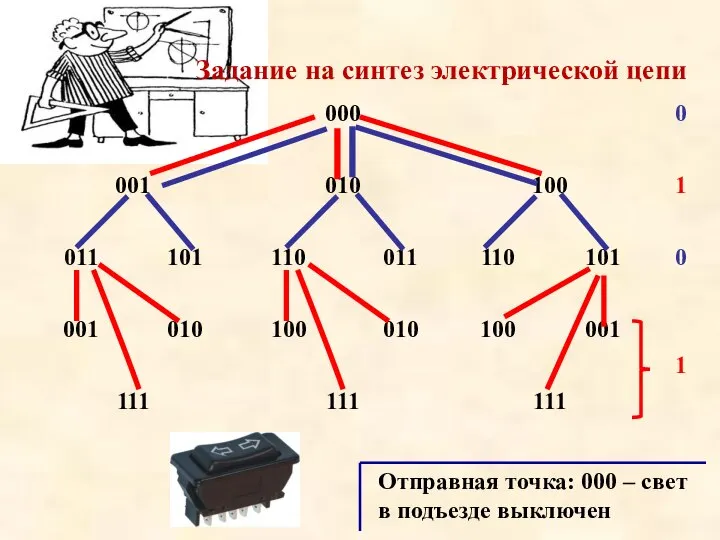
Слайд 34Отправная точка: 000 – свет в подъезде выключен
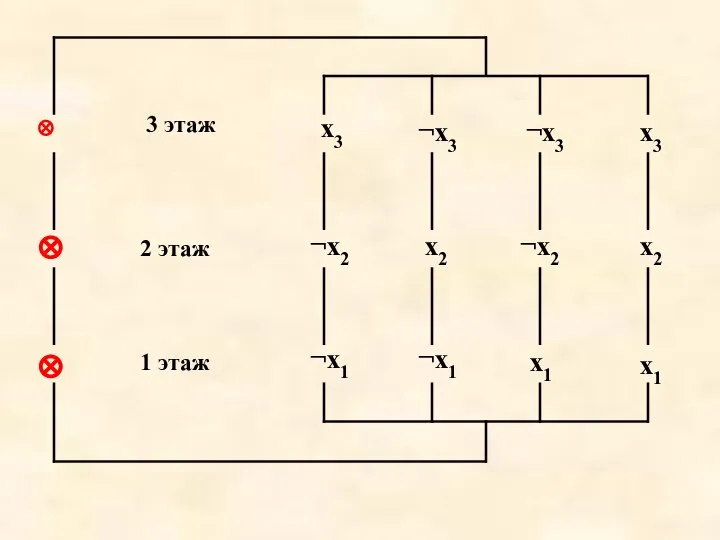
Слайд 36¬x1
¬x1
x1
x1
¬x2
¬x2
x2
x2
¬x3
¬x3
x3
x3
⊗
⊗
⊗
1 этаж
2 этаж
3 этаж
Слайд 40(Было 24, осталось 16 неизвестных)

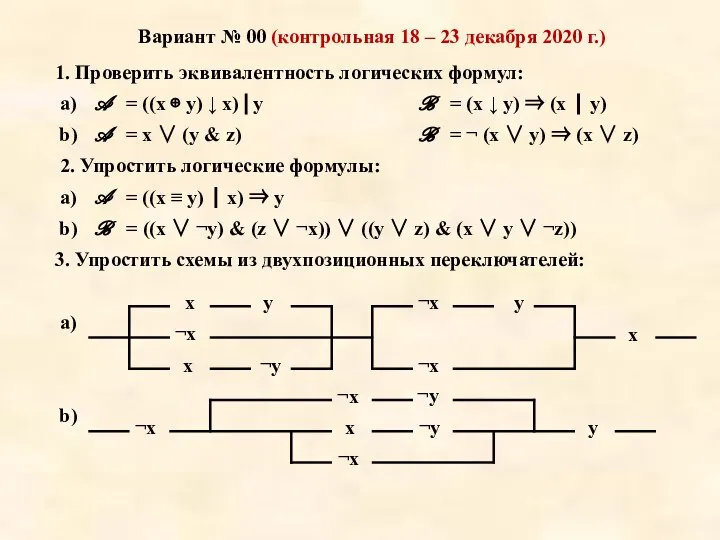
Слайд 43Контрольная работа: 18 - 23 декабря
Подведение итогов: 25 - 30 декабря

Слайд 46Можно видеть, что формулы A и B представляют одну и ту же
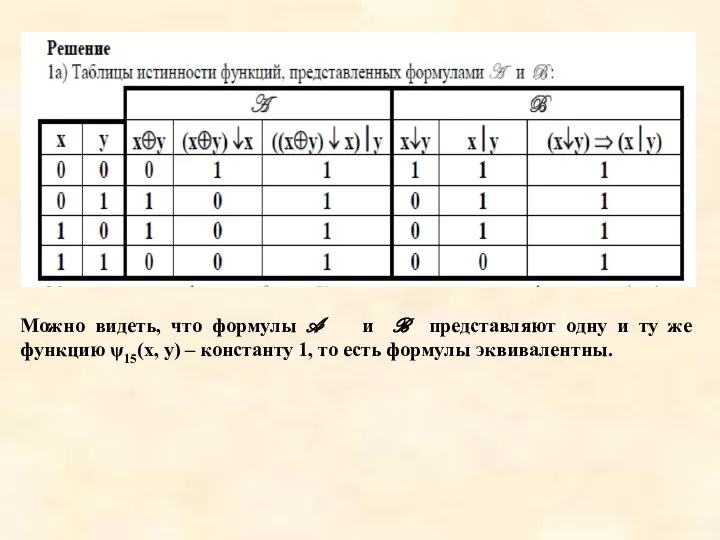
функцию ψ15(x, y) – константу 1, то есть формулы эквивалентны.
Слайд 47Можно видеть, что формула A представляет функцию η31(x, y, z), а формула
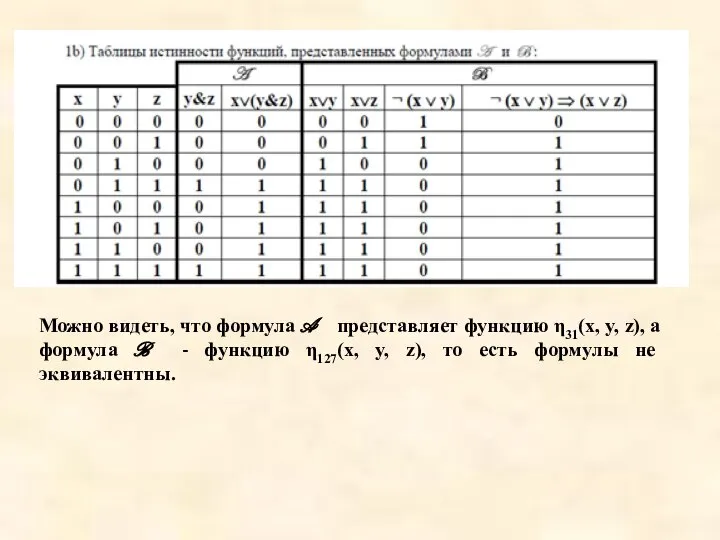
B - функцию η127(x, y, z), то есть формулы не эквивалентны.
Слайд 482a) ((x ≡ y) │ x) ⇒ y =
= (((x ∨ ¬y)
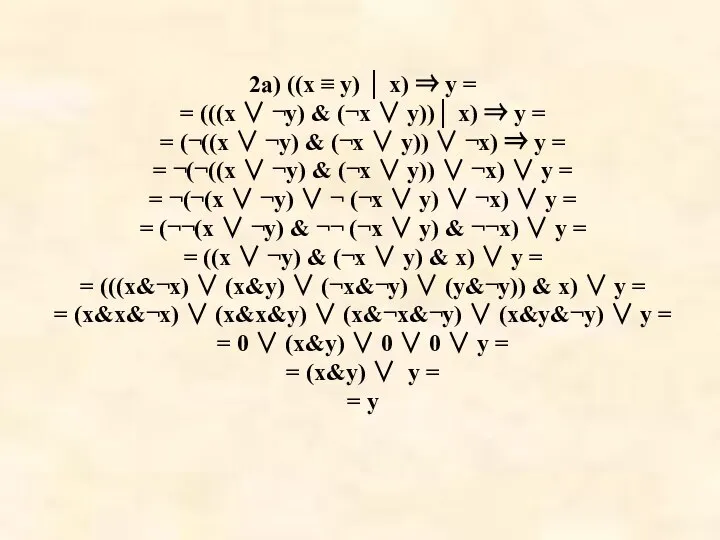
& (¬x ∨ y))│ x) ⇒ y =
= (¬((x ∨ ¬y) & (¬x ∨ y)) ∨ ¬x) ⇒ y =
= ¬(¬((x ∨ ¬y) & (¬x ∨ y)) ∨ ¬x) ∨ y =
= ¬(¬(x ∨ ¬y) ∨ ¬ (¬x ∨ y) ∨ ¬x) ∨ y =
= (¬¬(x ∨ ¬y) & ¬¬ (¬x ∨ y) & ¬¬x) ∨ y =
= ((x ∨ ¬y) & (¬x ∨ y) & x) ∨ y =
= (((x&¬x) ∨ (x&y) ∨ (¬x&¬y) ∨ (y&¬y)) & x) ∨ y =
= (x&x&¬x) ∨ (x&x&y) ∨ (x&¬x&¬y) ∨ (x&y&¬y) ∨ y =
= 0 ∨ (x&y) ∨ 0 ∨ 0 ∨ y =
= (x&y) ∨ y =
= y
Слайд 492b) ((x ∨ ¬y) & (z ∨ ¬x)) ∨ ((y ∨ z)
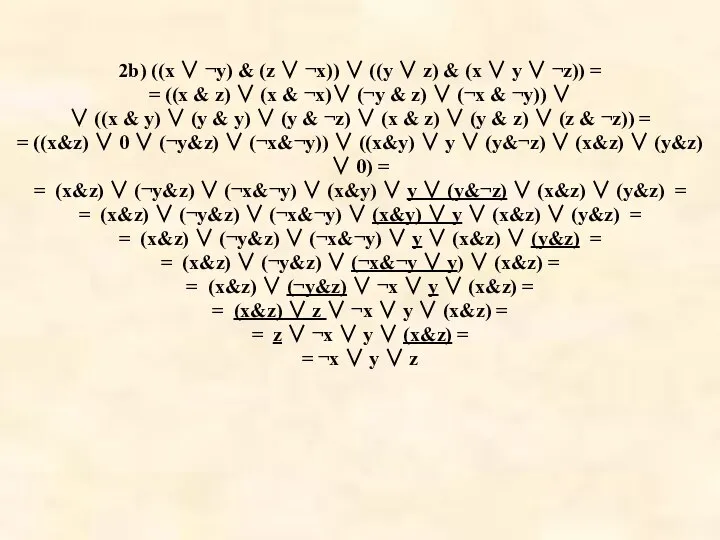
& (x ∨ y ∨ ¬z)) =
= ((x & z) ∨ (x & ¬x)∨ (¬y & z) ∨ (¬x & ¬y)) ∨
∨ ((x & y) ∨ (y & y) ∨ (y & ¬z) ∨ (x & z) ∨ (y & z) ∨ (z & ¬z)) =
= ((x&z) ∨ 0 ∨ (¬y&z) ∨ (¬x&¬y)) ∨ ((x&y) ∨ y ∨ (y&¬z) ∨ (x&z) ∨ (y&z) ∨ 0) =
= (x&z) ∨ (¬y&z) ∨ (¬x&¬y) ∨ (x&y) ∨ y ∨ (y&¬z) ∨ (x&z) ∨ (y&z) =
= (x&z) ∨ (¬y&z) ∨ (¬x&¬y) ∨ (x&y) ∨ y ∨ (x&z) ∨ (y&z) =
= (x&z) ∨ (¬y&z) ∨ (¬x&¬y) ∨ y ∨ (x&z) ∨ (y&z) =
= (x&z) ∨ (¬y&z) ∨ (¬x&¬y ∨ y) ∨ (x&z) =
= (x&z) ∨ (¬y&z) ∨ ¬x ∨ y ∨ (x&z) =
= (x&z) ∨ z ∨ ¬x ∨ y ∨ (x&z) =
= z ∨ ¬x ∨ y ∨ (x&z) =
= ¬x ∨ y ∨ z











































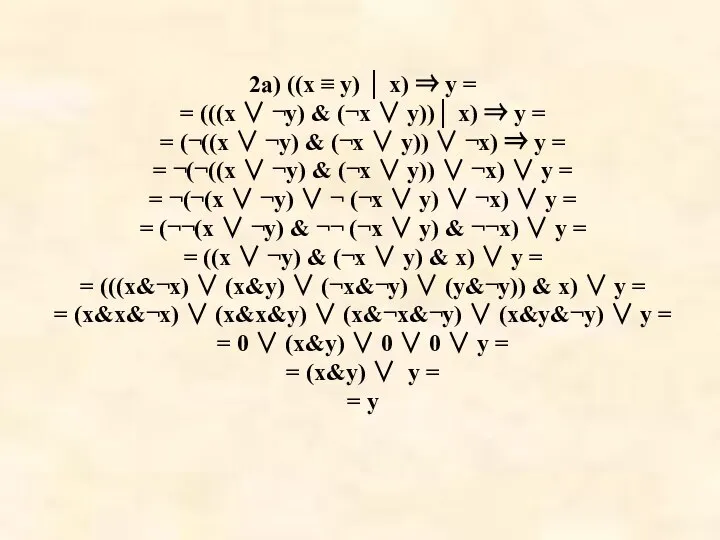
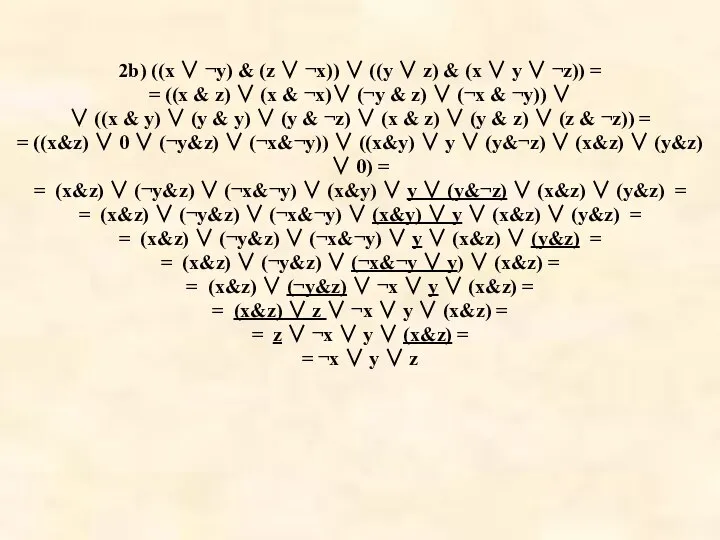
 Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях
Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях Методы и приемы решения дробно-рациональных уравнений, содержащих параметр
Методы и приемы решения дробно-рациональных уравнений, содержащих параметр Декартова система координат на плоскости. Математика, 6 класс
Декартова система координат на плоскости. Математика, 6 класс Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Цифровая азбука
Цифровая азбука Теоремы синусов и косинусов
Теоремы синусов и косинусов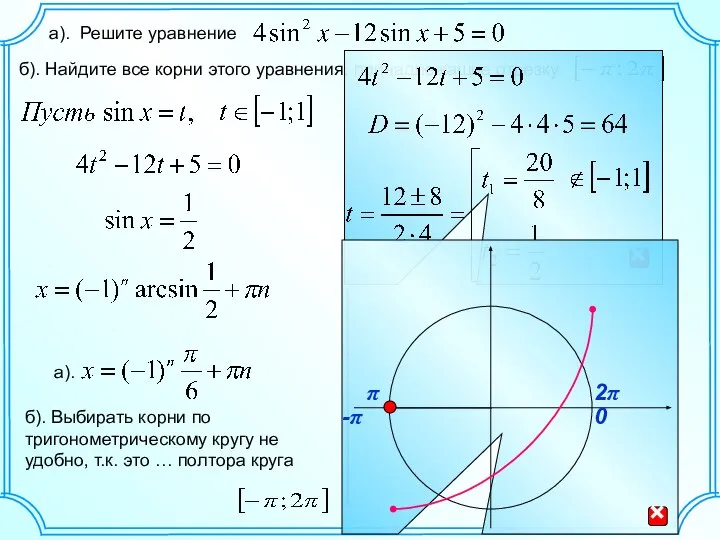 Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Закон Ома. Решение задач
Закон Ома. Решение задач Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел
Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел Площадь полной поверхности призмы
Площадь полной поверхности призмы Комбинаторные задачи
Комбинаторные задачи Радианная мера угла
Радианная мера угла Основные тригонометрические тождества. Формулы приведения
Основные тригонометрические тождества. Формулы приведения Vorlesung. Blatt 2
Vorlesung. Blatt 2 Соста числа 11
Соста числа 11 Тригонометрические уравнения
Тригонометрические уравнения Презентация на тему Стандартный вид числа 9 класс
Презентация на тему Стандартный вид числа 9 класс  Лекция 0
Лекция 0 Элементы математической статистики, комбинаторики и теории вероятностей
Элементы математической статистики, комбинаторики и теории вероятностей Презентация на тему Плоскость. Прямая. Луч
Презентация на тему Плоскость. Прямая. Луч  Симметрия. 9 класс
Симметрия. 9 класс Алгоритм Евклида
Алгоритм Евклида Второй и третий признаки равенства треугольников
Второй и третий признаки равенства треугольников Призмы. Виды призм
Призмы. Виды призм Приключения Буратино в Стране Финансов
Приключения Буратино в Стране Финансов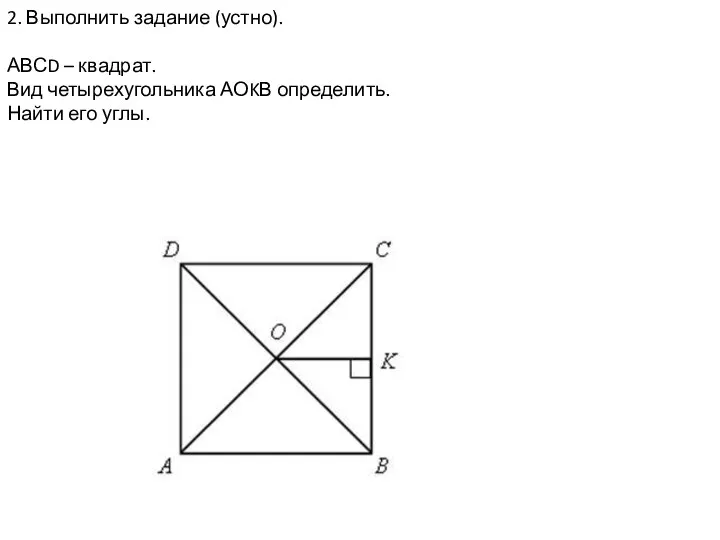 Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Периметр и площадь
Периметр и площадь Матрицы и определители
Матрицы и определители