Содержание
- 3. Треугольник Паскаля 1
- 5. Перестановки без повторений — комбинаторные соединения, которые могут отличаться друг от друга лишь порядком входящих в
- 6. (по первой букве французского слова arrangement – размещение) к Размещения Размещение из n элементов по k.
- 7. Сочетания Число сочетаний из n элементов по k. (по первой букве французского слова Сombination – сочетание).
- 8. Решение задач
- 9. Решение задач
- 14. 5. 6. 7.
- 21. Вероятность того, что батарейка бракованная равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две
- 22. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите
- 24. Р = 0,2∙0,7 + 0,2∙0,3 + 0,8∙0,3 = 0,44 П1и М1 или П1иП2 или М1иП2 П1-попал
- 26. В торговом центре два одинаковых автомата продают кофе. К концу дня в отдельно взятом автомате, кофе
- 28. Построим серединный перпендикуляр к отрезку ОС.
- 39. Скачать презентацию





























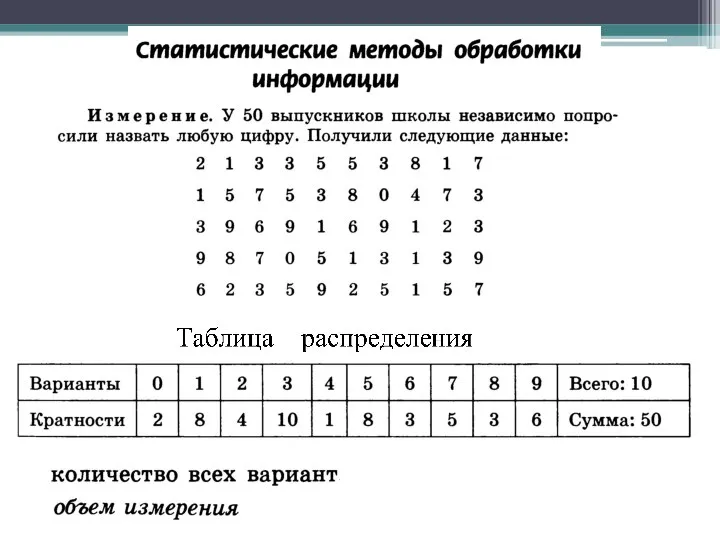
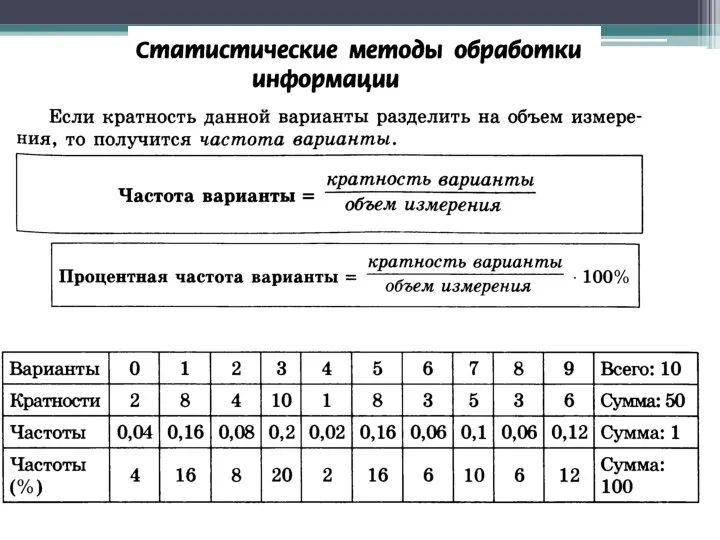
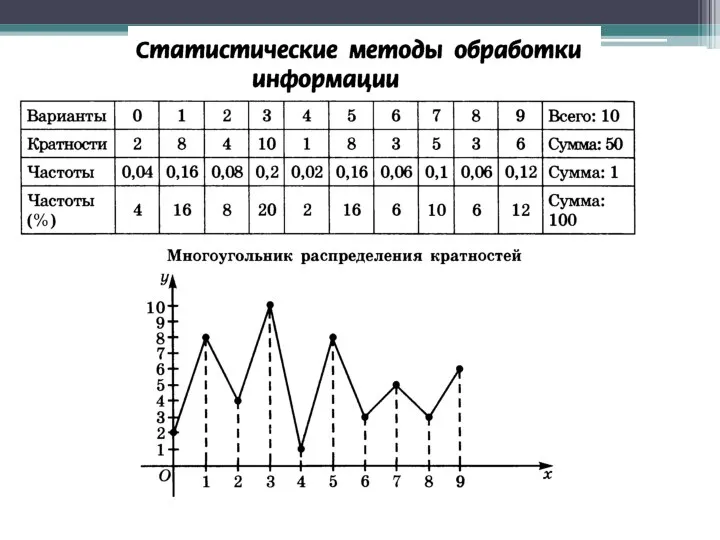
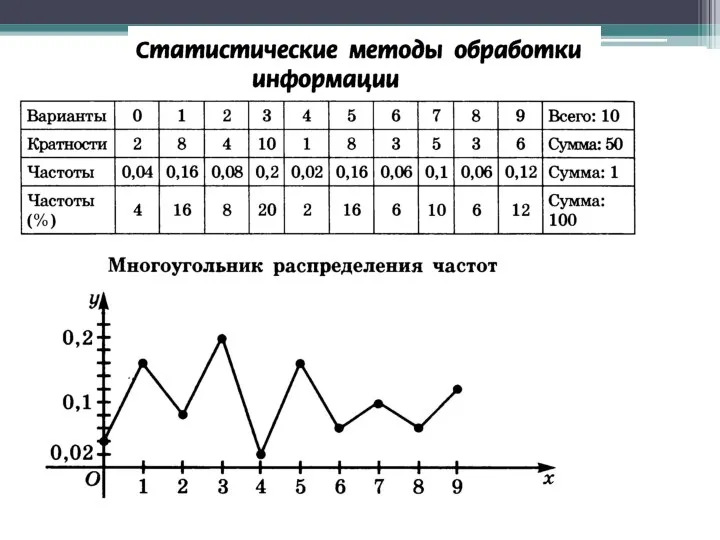
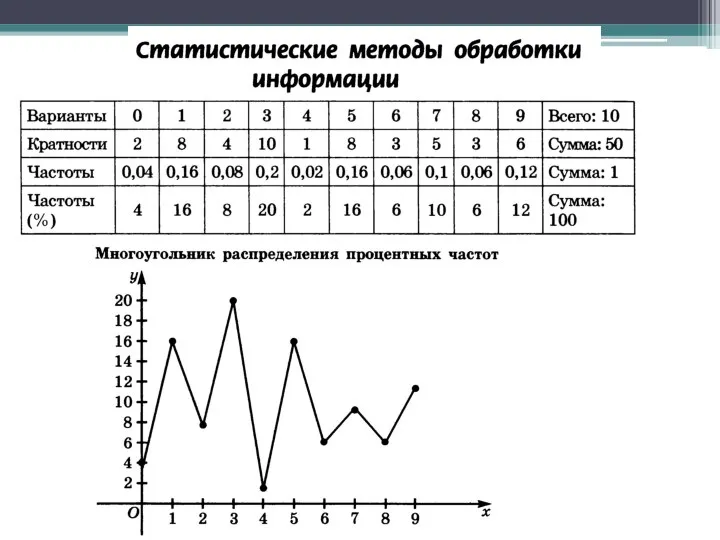
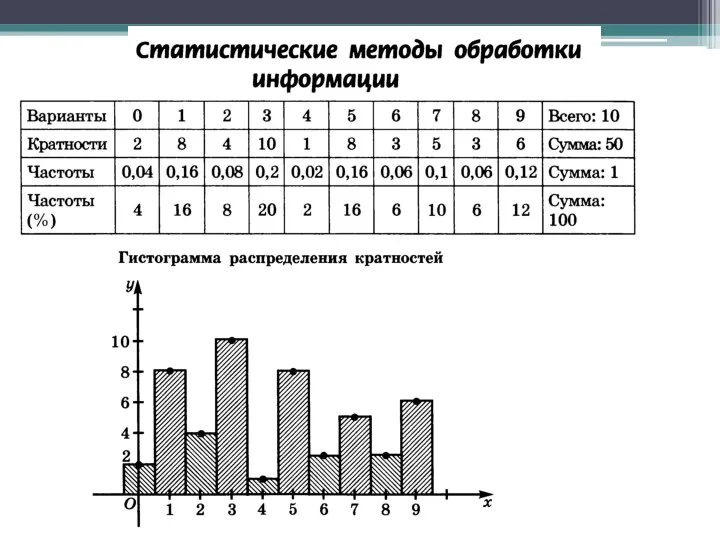
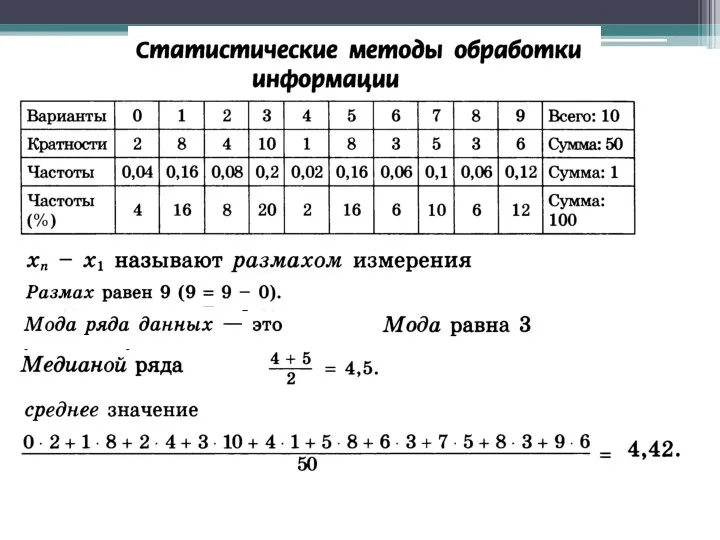
 Применение инверсии при построении графиков
Применение инверсии при построении графиков Решение задач по теме: Параллелограмм (1)
Решение задач по теме: Параллелограмм (1) Презентация на тему Римские цифры (3 класс)
Презентация на тему Римские цифры (3 класс)  Построение графика функции, используя её свойства
Построение графика функции, используя её свойства Построение графиков функций с помощью производных
Построение графиков функций с помощью производных Эволюционные этапы развития логистики
Эволюционные этапы развития логистики параллельность
параллельность Геометрические фигуры вокруг нас
Геометрические фигуры вокруг нас Математика и здоровье. Математика и медицина
Математика и здоровье. Математика и медицина Решение задач с помощью уравнений. Алгебра. 7 класс. Ю.М. Колягин и др
Решение задач с помощью уравнений. Алгебра. 7 класс. Ю.М. Колягин и др Памятки по математике
Памятки по математике Презентация на тему Меры длинны Древней Руси
Презентация на тему Меры длинны Древней Руси  Obratnye_trigonometricheskie_funktsii (1)
Obratnye_trigonometricheskie_funktsii (1) Равенство, неравенство. Устный счет (1 класс)
Равенство, неравенство. Устный счет (1 класс) 27.09 Графики функций
27.09 Графики функций Весёлые клоуны. Игра по математике для 1 класса
Весёлые клоуны. Игра по математике для 1 класса Разложите многочлены на множители
Разложите многочлены на множители Устный счет в пределах 10. Состав чисел 7, 8
Устный счет в пределах 10. Состав чисел 7, 8 Инварианты. Систематизация задач на инварианты по типам
Инварианты. Систематизация задач на инварианты по типам Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Математика. Учебный 2022 год с Марусей
Математика. Учебный 2022 год с Марусей Решение задач по теме Теорема Пифагора
Решение задач по теме Теорема Пифагора Площадь и объём фигуры
Площадь и объём фигуры Решение задач
Решение задач Обобщающее повторение. Алгебра 11 класс
Обобщающее повторение. Алгебра 11 класс Измерение длины отрезка
Измерение длины отрезка Координатный луч
Координатный луч Величины. Длина
Величины. Длина