Слайд 2В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может

иметь место лишь при замене одного объекта другим, точно таким же.
При моделировании абсолютное подобие не имеет места.
Исследователи стремятся к тому, чтобы модель достаточно хорошо отображала исследуемую сторону функционирования объектов.
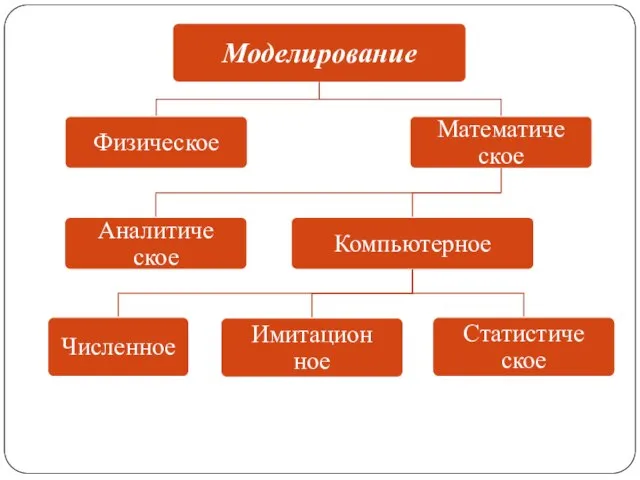
Слайд 4Физическое моделирование
Модель воспроизводит изучаемую систему (оригинал) с сохранением его физической природы.
Задаются

некоторые характеристики внешней среды, и исследуется поведение объекта или системы при заданных или создаваемых искусственно воздействиях внешней среды.
Физическое моделирование может протекать в реальных или нереальных масштабах времени, а также без учета времени.
Слайд 5Математическое моделирование
Способ исследования различных процессов путем изучения явлений, имеющих различное физическое содержание,

но описываемых одинаковыми математическими отношениями.
Вид математической модели зависит как от природы реального объекта (системы), так и задач исследования, а также требуемой достоверности и точности решения задачи.
Слайд 6Компьютерное моделирование
Метод решения задач анализа или синтеза сложной системы на основе использования

ее компьютерной модели.
Модель формируется в виде алгоритма и программы для реализации математической модели на ЭВМ. Это позволяет проводить над моделью вычислительные эксперименты и получать количественные и качественные результаты.
Качественные результаты анализа обнаруживают неизвестные ранее свойства сложной системы: ее структуру, динамику развития, устойчивость, целостность и др. Количественные выводы в основном носят характер анализа существующей сложной системы или прогноза будущих значений некоторых переменных.
Слайд 7Аналитическое моделирование
Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются

в виде некоторых функциональных соотношений – алгебраических, интегрально-функциональных, конечно-разностных и т. д.
Аналитическая модель может быть исследована следующими методами:
аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик;
численным, когда решение получают в виде числовых результатов при конкретных начальных данных;
качественным, когда, не имея решения в явном виде, стараются найти некоторые свойства решения.





 Презентация на тему Нахождение площадей ромба, параллелограмма
Презентация на тему Нахождение площадей ромба, параллелограмма  Как математика учит критическому мышлению
Как математика учит критическому мышлению Граф – набор точек, некоторые из которых соединены линиями
Граф – набор точек, некоторые из которых соединены линиями Параллельные прямые
Параллельные прямые Умножение двузначных чисел
Умножение двузначных чисел Десятичные дроби по-английски. Бинарный урок
Десятичные дроби по-английски. Бинарный урок Симметрия относительно точки
Симметрия относительно точки Удивительный мир математики
Удивительный мир математики Преобразование графиков функций
Преобразование графиков функций Производная в ЕГЭ
Производная в ЕГЭ Законы булевой алгебры
Законы булевой алгебры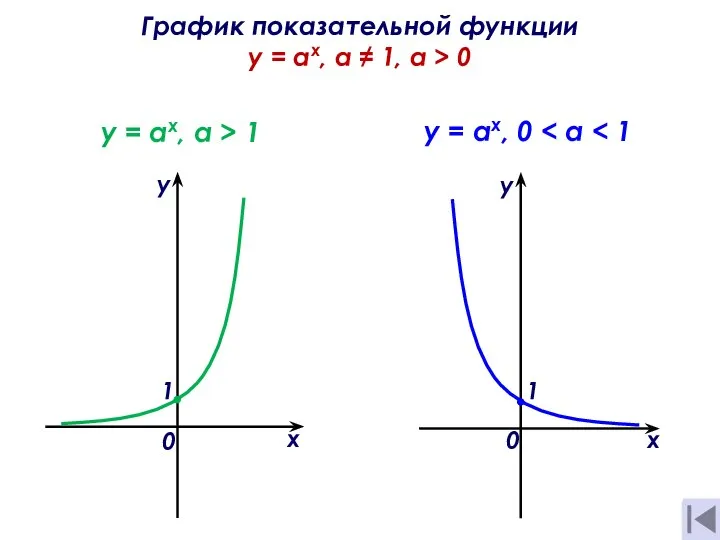 Показательные неравенства и уравнения
Показательные неравенства и уравнения Производная произведения двух функций
Производная произведения двух функций Цилиндр. Сечения цилиндра
Цилиндр. Сечения цилиндра Презентация на тему Формирование УУД на уроках математики в 5 классе
Презентация на тему Формирование УУД на уроках математики в 5 классе  Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями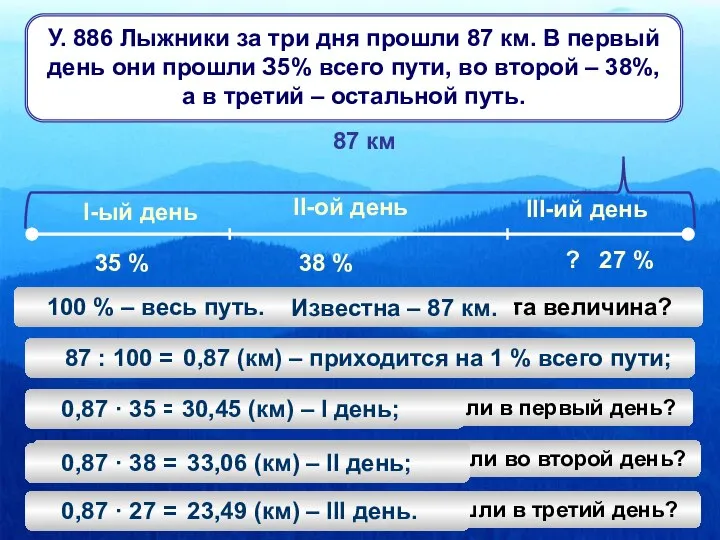 Задачи о лыжниках
Задачи о лыжниках Приём деления для случаев вида: 87: 29, 66 : 22
Приём деления для случаев вида: 87: 29, 66 : 22 Пифагория. Геометрия в клетках. Геймификация обучения
Пифагория. Геометрия в клетках. Геймификация обучения Признаки равенства треугольников
Признаки равенства треугольников Иррациональные неравенства и способы их решения
Иррациональные неравенства и способы их решения Шкала. Координатный луч
Шкала. Координатный луч Формы работы при подготовке к ЕГЭ
Формы работы при подготовке к ЕГЭ Комбинаторика
Комбинаторика Презентация на тему Шутка гениев: флексагон
Презентация на тему Шутка гениев: флексагон  Измерение и построение углов
Измерение и построение углов Решение уравнений. Тест
Решение уравнений. Тест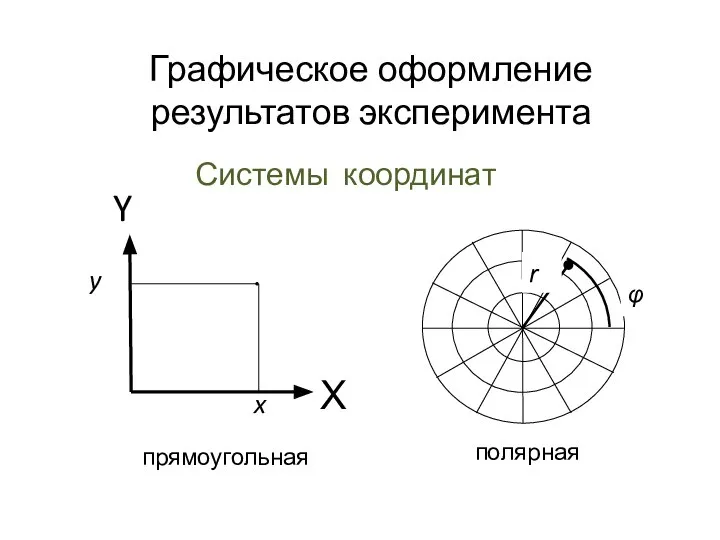 Графическое оформление результатов эксперимента
Графическое оформление результатов эксперимента