Слайд 2Властивості задачі лінійного програмування
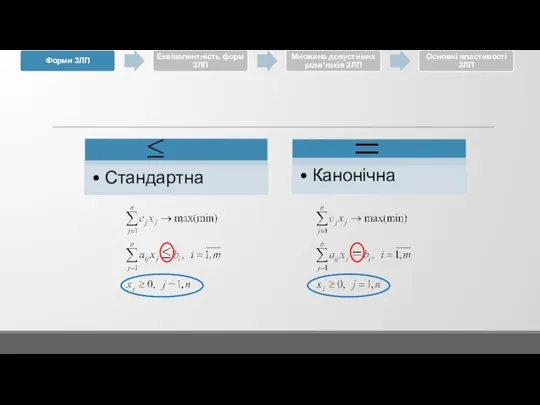
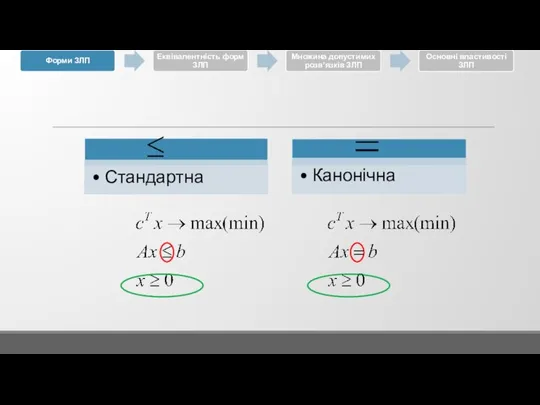
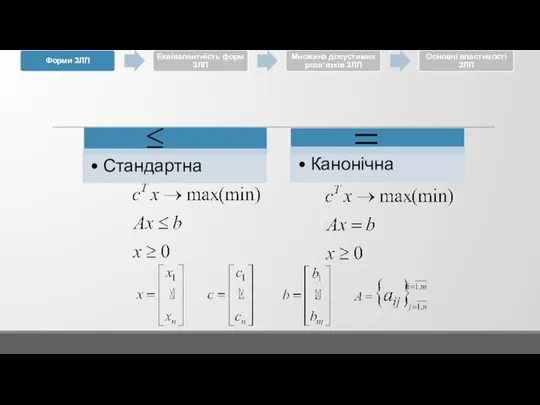
3.1 Форми ЗЛП
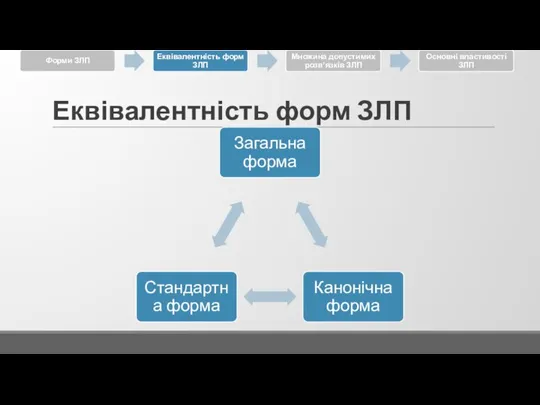
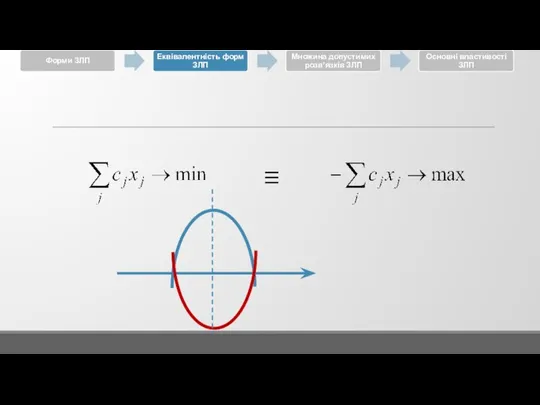
3.2 Еквівалентність форм ЗЛП
3.3 Множина допустимих розв’язків

ЗЛП (багатогранні множини, багатогранники, вершини, грані)
3.4 Основні властивості ЗЛП і теореми лінійного програмування
Слайд 3Задача лінійного програмування (ЗЛП)

Слайд 4Задача лінійного програмування (ЗЛП)

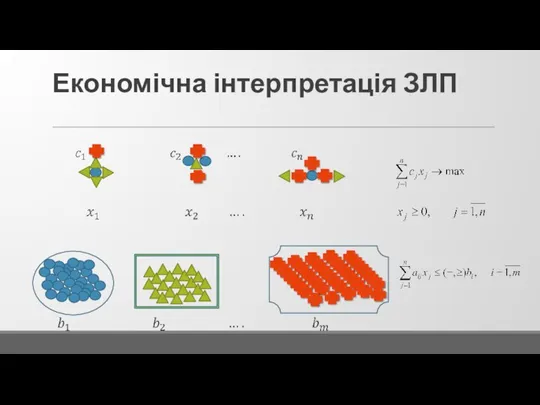
Слайд 5Економічна інтерпретація ЗЛП
Слайд 6Основні припущення
1) пропорційність,
2) адитивність,
3) невід’ємність
Пропорційність означає, що витрати ресурсів на деякий вид

продукції прямо пропорційні його обсягу випуску, а вклад цього виду продукції в ЦФ також прямо пропорційний його обсягу випуску.
Адитивність означає, що загальна величина ресурсу, використовуваного на виробництво всіх видів продукції, дорівнює сумі витрат цього ресурсу на окремі види продукції. Аналогічно інтерпретується і ЦФ.
Самостійно №1 Навести приклади проблемних ситуацій, в яких порушені ці припущення
Слайд 11Саме для канонічної ЗЛП розроблено метод розв’язання
Далі будемо розглядати задачі на максимум

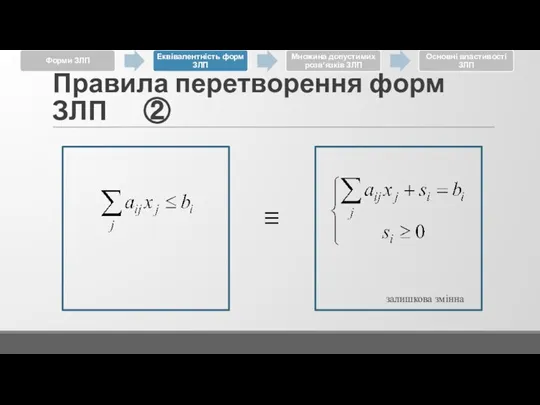
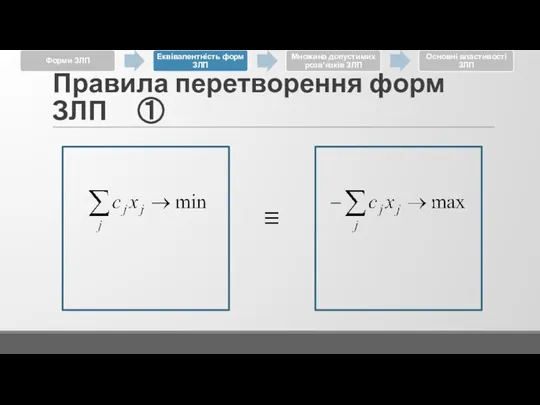
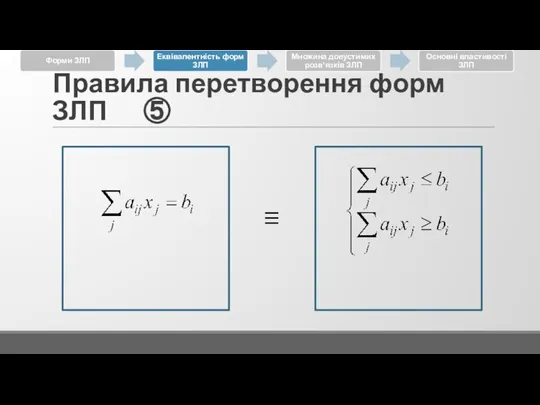
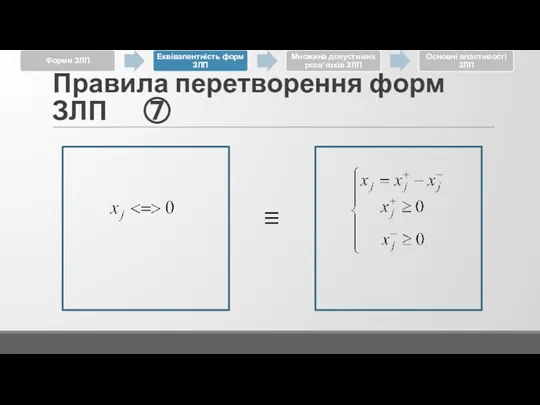
Слайд 15Правила перетворення форм ЗЛП ②
залишкова змінна
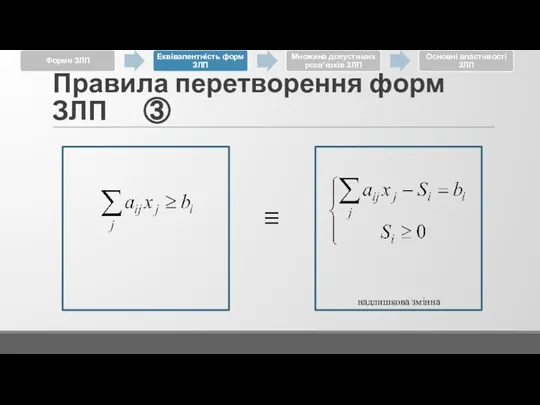
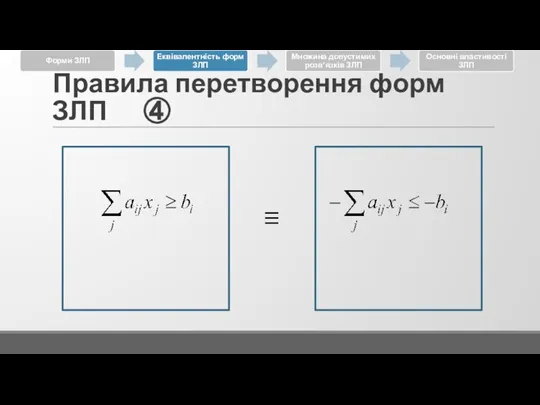
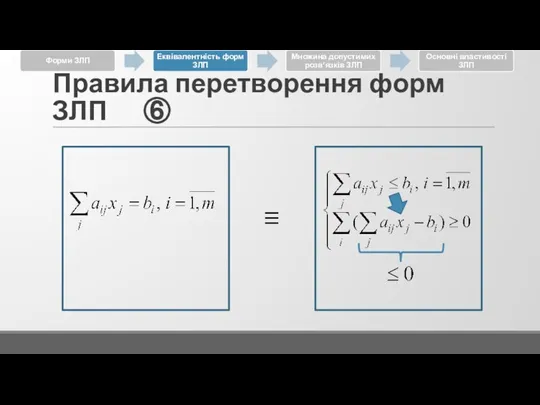
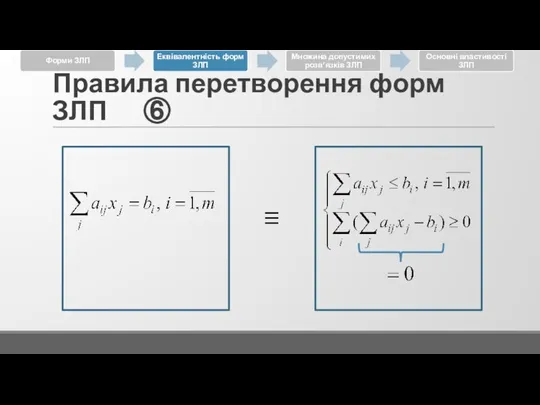
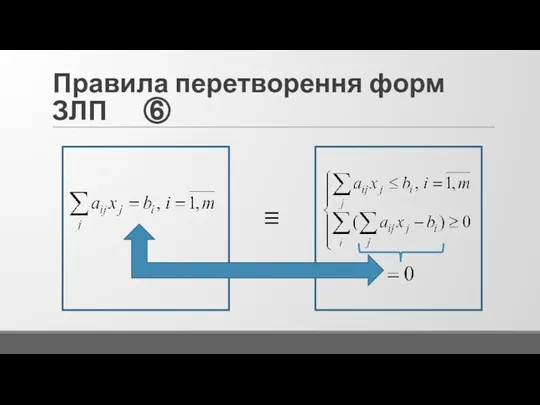
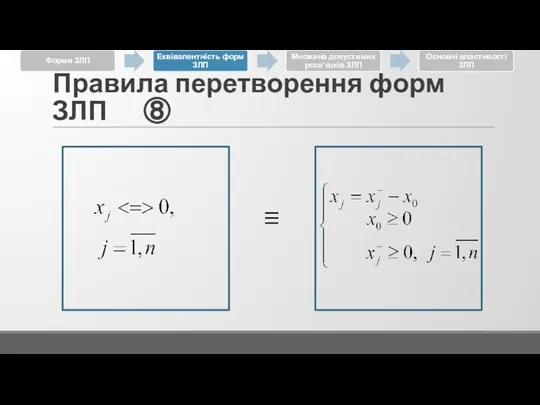
Слайд 16Правила перетворення форм ЗЛП ③
надлишкова змінна
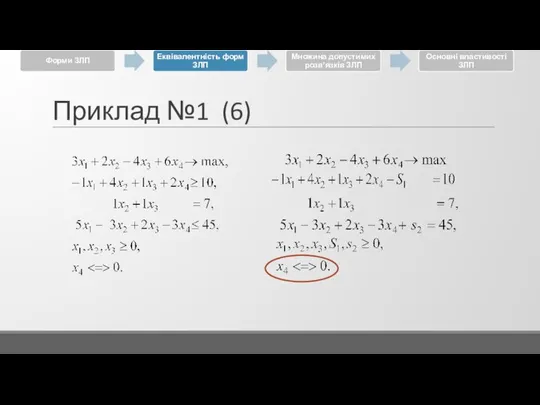
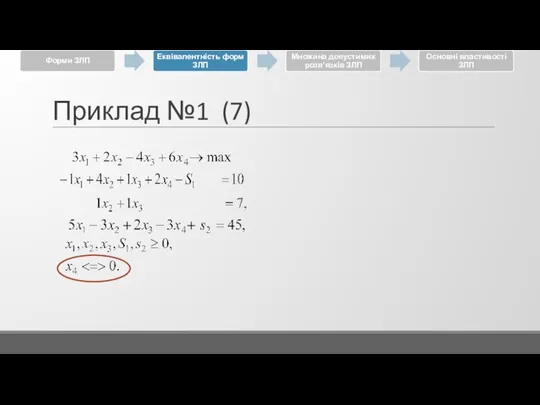
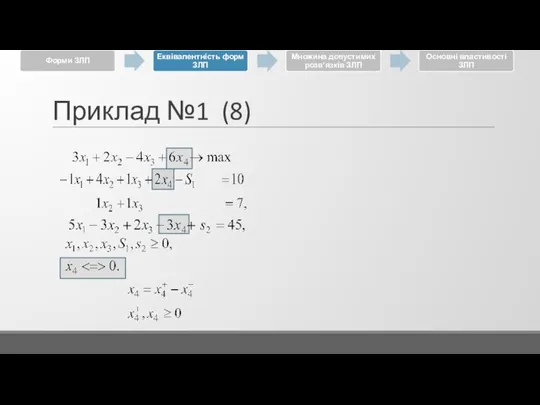
Слайд 24Приклад №1 (1)
Привести задачу до КФ

Слайд 25Приклад №1 (2)
КАНОНІЧНА ФОРМА
Не відповідають КФ

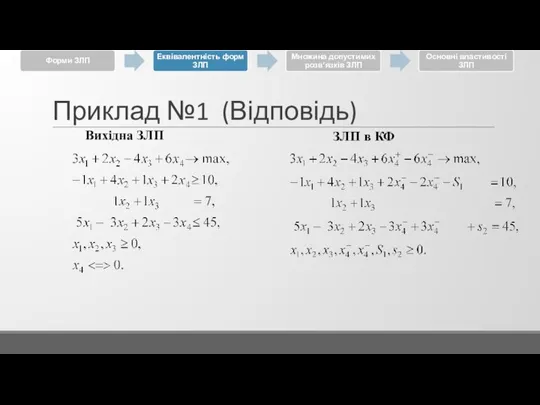
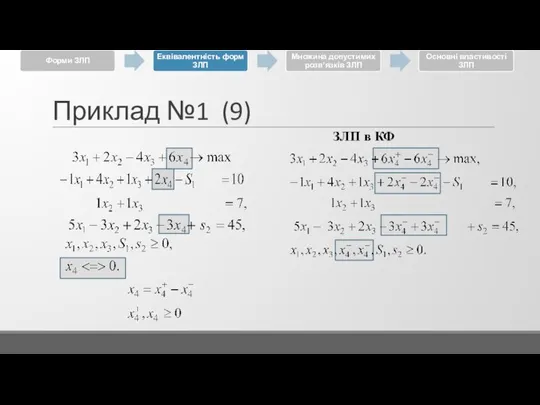
Слайд 36Приклад №1 (Відповідь)
ЗЛП в КФ
Вихідна ЗЛП
Слайд 37
Зведення ЗЛП в стандартній формі до канонічної
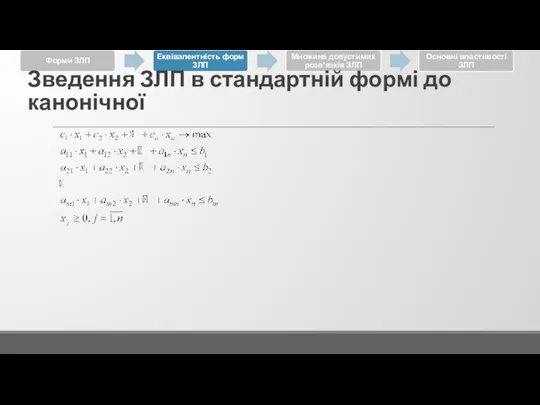
Слайд 38Зведення ЗЛП в стандартній формі до канонічної
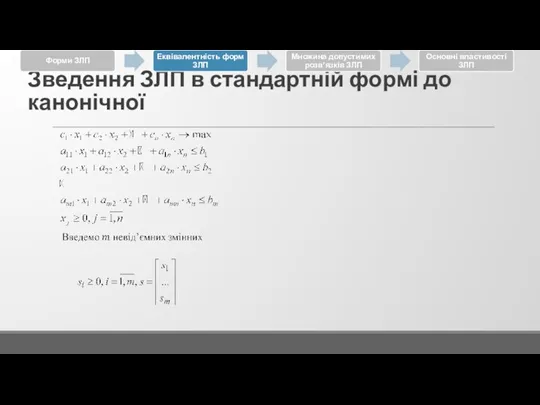
Слайд 39
Зведення ЗЛП в стандартній формі до канонічної
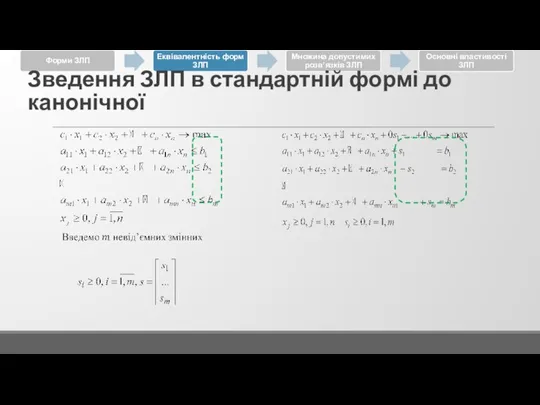
Слайд 40
Зведення ЗЛП в стандартній формі до канонічної
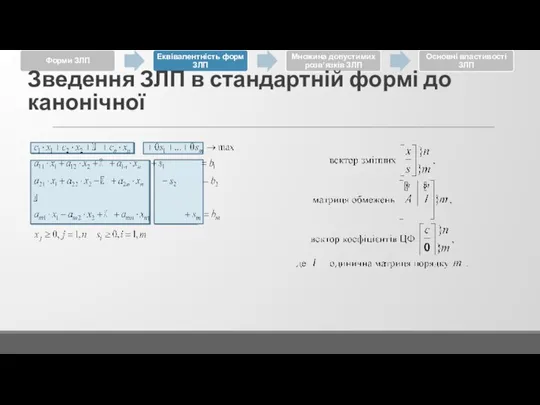
Слайд 41Вихідна ЗЛП в СФ ЗЛП в КФ
Зведення ЗЛП в стандартній формі до
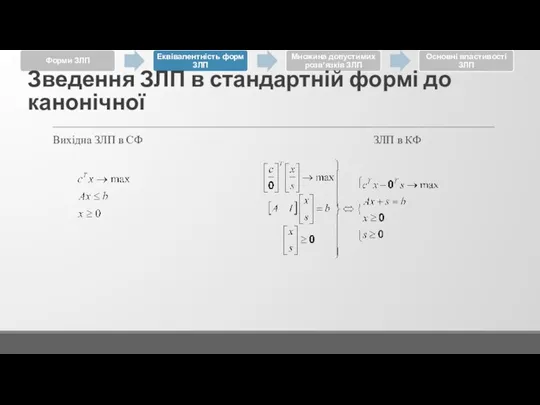
канонічної
Слайд 42Приклад №2 зведення до КФ
Вихідна ЗЛП:
z = 5x1 + 6x2 → max
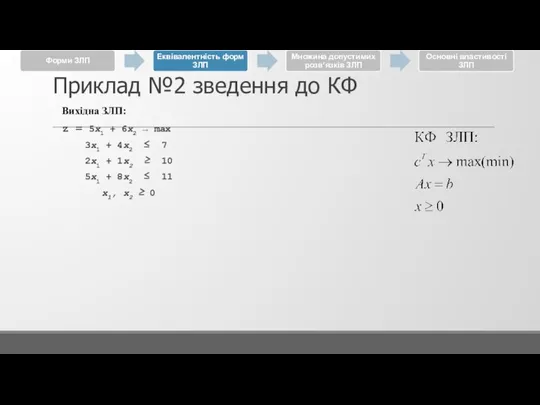
3x1 + 4x2 ≤ 7
2x1 + 1x2 ≥ 10
5x1 + 8x2 ≤ 11
x1, x2 ≥ 0
Слайд 43Приклад №2 зведення до КФ
Вихідна ЗЛП:
z = 5x1 + 6x2 → max

3x1 + 4x2 ≤ 7
2x1 + 1x2 ≥ 10
5x1 + 8x2 ≤ 11
x1, x2 ≥ 0
ЗЛП в канонічній формі:
z = 5x1 + 6x2 + 0s1 + 0s2 + 0s3 → max
3x1 + 4x2 + s1 = 7
2x1 + 1x2 - s2 = 10
5x1 + 8x2 + s3 = 11
x1, x2, s1, s2, s3 ≥ 0
Слайд 44Приклад №3 зведення до КФ
Вихідна ЗЛП:
z = 3x1 + 9x2 → min
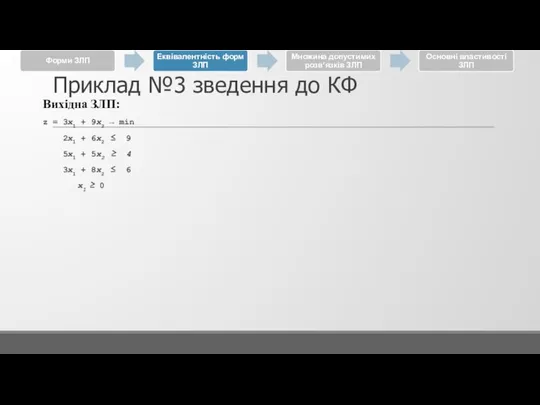
2x1 + 6x2 ≤ 9
5x1 + 5x2 ≥ 4
3x1 + 8x2 ≤ 6
x1 ≥ 0
Слайд 45Приклад №3 зведення до КФ
Вихідна ЗЛП:
z = 3x1 + 9x2 → min
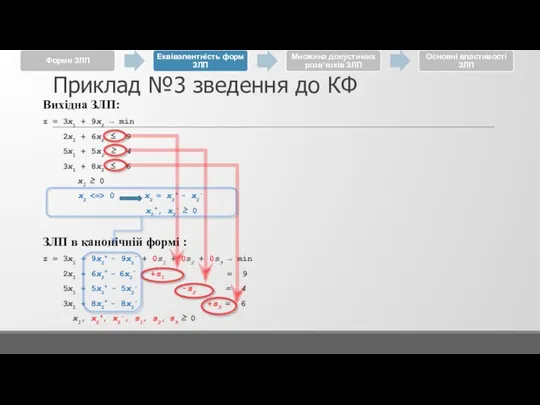
2x1 + 6x2 ≤ 9
5x1 + 5x2 ≥ 4
3x1 + 8x2 ≤ 6
x1 ≥ 0
x2 <=> 0 x2 = x2+ - x2-
x2+, x2- ≥ 0
ЗЛП в канонічній формі :
z = 3x1 + 9x2+ - 9x2- + 0s1 + 0s2 + 0s3 → min
2x1 + 6x2+ - 6x2- +s1 = 9
5x1 + 5x2+ - 5x2- -s2 = 4
3x1 + 8x2+ - 8x2- +s3 = 6
x1, x2+, x2-, s1, s2, s3 ≥ 0
Слайд 46Екзаменаційне завдання А
min z = 9x1 − 3x2
2x1 + 8x2 −
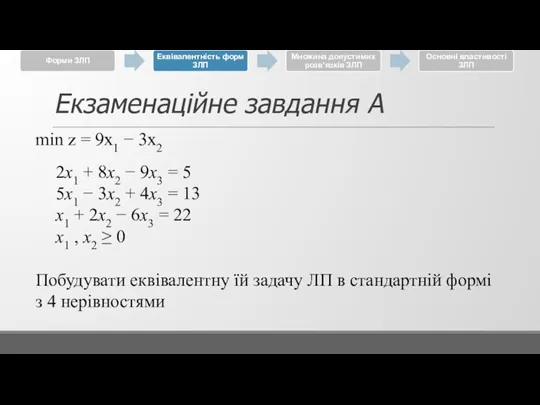
9x3 = 5
5x1 − 3x2 + 4x3 = 13
x1 + 2x2 − 6x3 = 22
x1 , x2 ≥ 0
Побудувати еквівалентну їй задачу ЛП в стандартній формі з 4 нерівностями
Слайд 47Екзаменаційне завдання Б
min z = 9x1 − 3x2
2x1 + 8x2 −

9x3 = 5
5x1 − 3x2 + 4x3 = 13
x1 + 2x2 − 6x3 = 22
Побудувати еквівалентну їй задачу ЛП на максимум в стандартній формі з 5-ма нерівностями і 4-ма з мінними





























 Признаки параллелограмма. 8 класс
Признаки параллелограмма. 8 класс Неопределённый и определённый интеграл
Неопределённый и определённый интеграл Веселый паровоз. Мультимедийное пособие по математике
Веселый паровоз. Мультимедийное пособие по математике Проект Колодец. Деловая игра по теме Цилиндр
Проект Колодец. Деловая игра по теме Цилиндр Презентация на тему Деление многозначных чисел
Презентация на тему Деление многозначных чисел  Алгоритм вычислений
Алгоритм вычислений Логика
Логика Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8
Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8 Параллелограмм и трапеция. Урок 6
Параллелограмм и трапеция. Урок 6 Пирамида. Виды пирамид
Пирамида. Виды пирамид Игра-тренажёр Округление чисел
Игра-тренажёр Округление чисел Вычисление одномерных, двумерных и интегралов c переменным верхним пределом
Вычисление одномерных, двумерных и интегралов c переменным верхним пределом Алгебра 10кл - Презентация к уроку 1 (Самойлова Г. А.)
Алгебра 10кл - Презентация к уроку 1 (Самойлова Г. А.) Правильные многогранники
Правильные многогранники Алгебраические выражения
Алгебраические выражения Логический элемент
Логический элемент Презентация на тему Вектор
Презентация на тему Вектор  Правила с двумя решениями. Подход Неймана – Пирсона
Правила с двумя решениями. Подход Неймана – Пирсона Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2»
Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2» Презентация на тему Отрезок. Графики
Презентация на тему Отрезок. Графики  Стереометрия 1. ЕГЭ
Стереометрия 1. ЕГЭ Окружность. 5 класс
Окружность. 5 класс Урок 14. Первый признак равенства треугольников
Урок 14. Первый признак равенства треугольников Сложение и вычитание вида ± 1, ± 2, ± 3 (1 класс)
Сложение и вычитание вида ± 1, ± 2, ± 3 (1 класс) Презентация на тему Римские цифры (3 класс)
Презентация на тему Римские цифры (3 класс)  Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Тестирование генераторов случайных чисел
Тестирование генераторов случайных чисел Презентация на тему Подготовка к ГИА 2013
Презентация на тему Подготовка к ГИА 2013