VSM_mag_2-16

Основные понятия
Случайная величина – принимает одно из множества значений; появление того или иного значения нельзя предсказать точно
Непрерывная случайная величина – может принимать все значения на некотором промежутке; множество возможных значений бесконечно
Дискретная случайная величина – принимает отдельные, изолированные значения с определенной вероятностью; их число может быть конечно или бесконечно

Порядок выбора ВСМ
Наблюдается случайная величина (статистика).
Обрабатывается статистика методами статистического анализа.
Выбирается ВСМ с учетом физической сущности исследуемого процесса.
Доказывается правомерность выбранной ВСМ по критериям согласия.
Определяются характеристики (параметры) ВСМ и по ним выполняют прогноз.

Задачи статистического анализа
Обработка экспериментальных данных
Определение вида закона распределения
Определение параметров закона распределения
Прогнозирование поведения случайной величины

Статистические характеристики случайной величины
n – объем выборки (количество наблюдений)
N – объем генеральной совокупности
n=N(полная выборка), n
Интервальная оценка
fi*(x)=Δni/n Δx
Pi* = Δni/n
Fi*(x)=ni(x)/n
Δni – количество наблюдений на интервале
Δx – величина интервала
ni(x) - количество наблюдений на начало интервала

Характеристики ВСМ на основе непрерывных случайных величин
Для случайной величины x:
F(x) - функция распределения
f(x) - плотность распределения
М.О.[x] – математическое ожидание
Д[x] – дисперсия
σx= - средне-квадратическое отклонение
ν= σx/М.О.[x] – коэффициент вариации

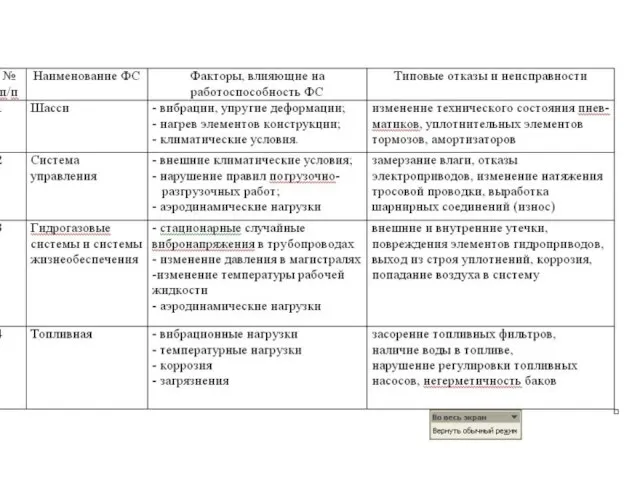
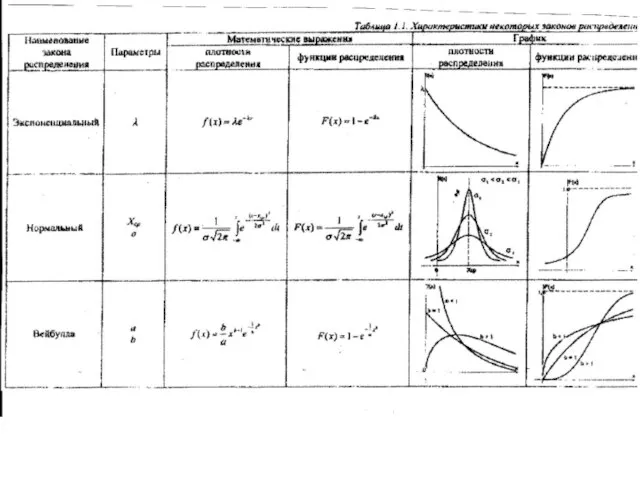
Законы распределения наработки до отказа

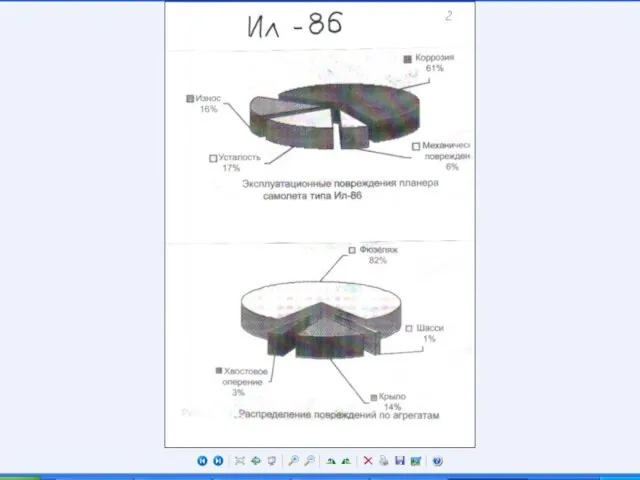
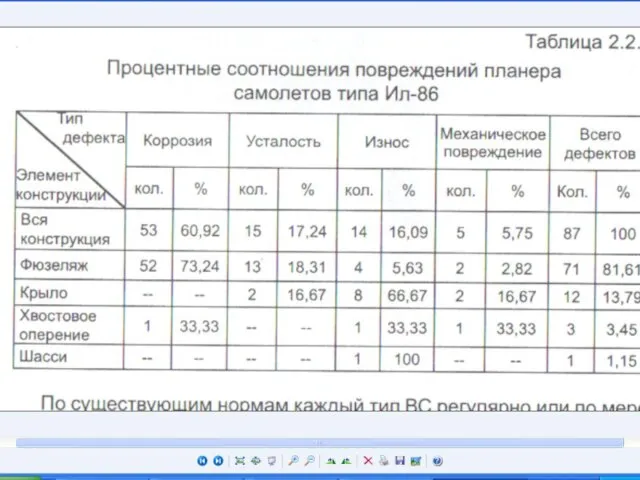
Применение законов распределения непрерывной случайной величины

Характеристики ВСМ на основе дискретных случайных величин

Законы распределения дискретных случайных величин

Обобщенные аналитические ВСМ

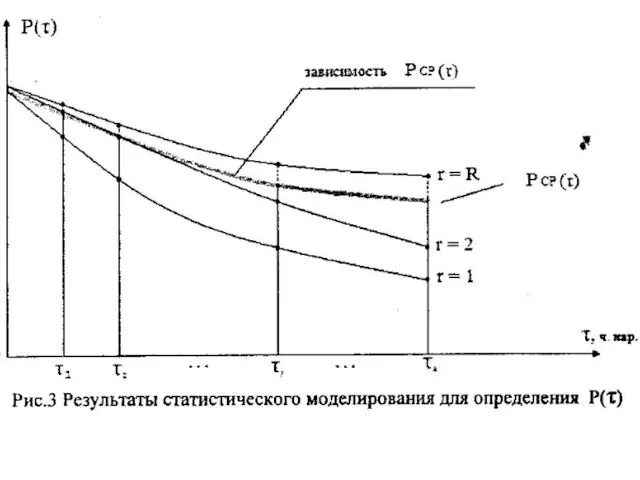
Метод статистического моделирования