Введение декартовых координат в пространстве. Формулы середины отрезка и расстояния между двумя точками
Содержание
- 2. Вспомним, как определяется координатная(числовая) прямая. Изображаем произвольную прямую; х 0 1 М а Тогда любой точки
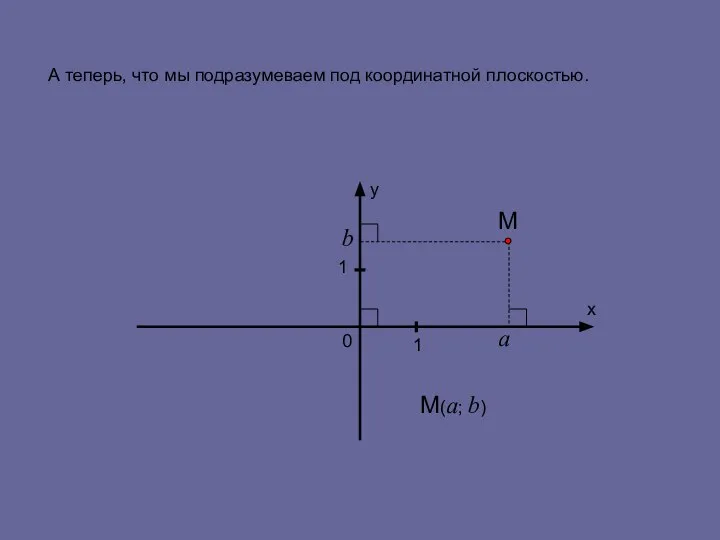
- 3. А теперь, что мы подразумеваем под координатной плоскостью. у х 0 1 1 М а b
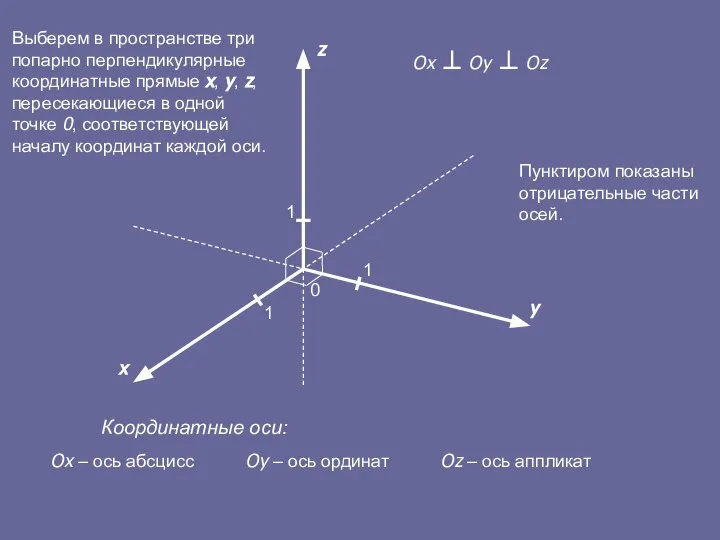
- 4. x y z 0 1 Ox ⊥ Oy ⊥ Oz Ox – ось абсцисс Oy –
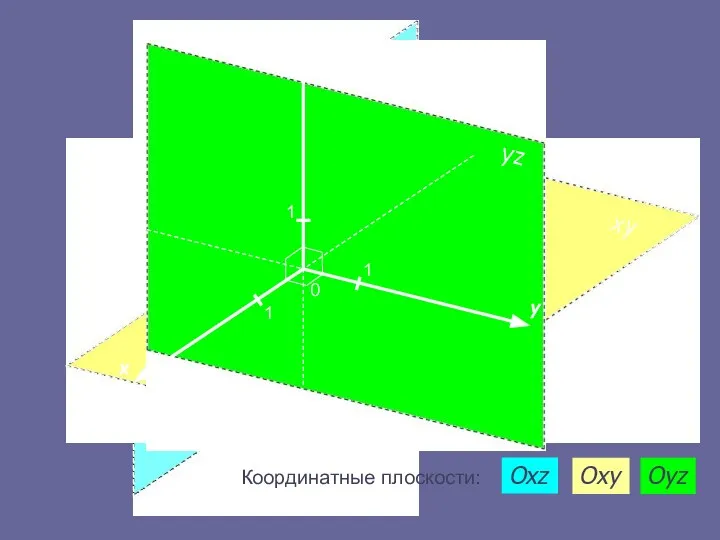
- 5. x y z 0 1 1 1 Координатные плоскости: Oxz Oxy Oyz
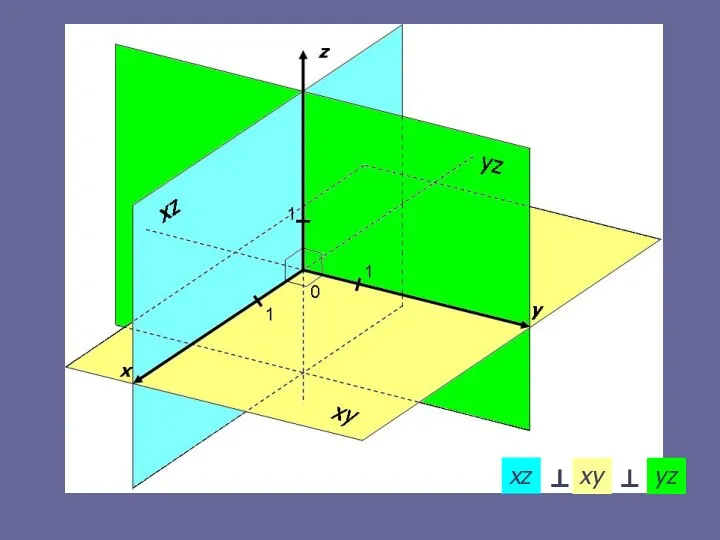
- 6. Координатные плоскости: xz ⊥ xy ⊥ yz
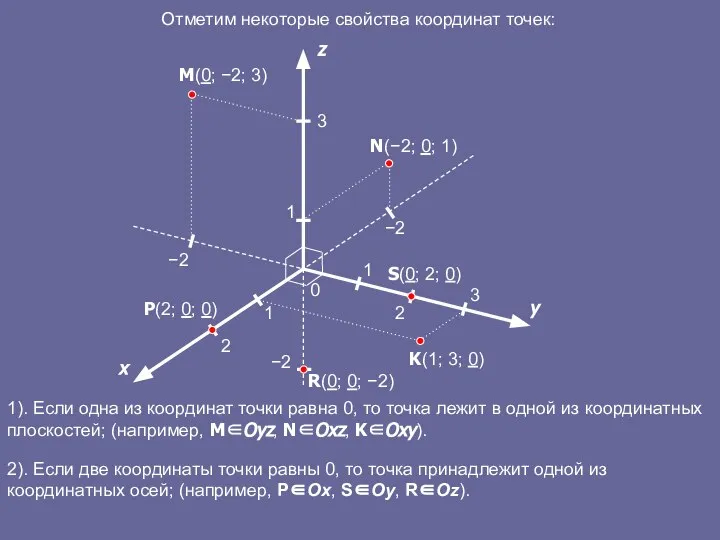
- 7. 1). Если одна из координат точки равна 0, то точка лежит в одной из координатных плоскостей;
- 8. Формулы середины отрезка и расстояния между точками на плоскости.
- 9. Задача №1. Найдите координаты середины отрезка АВ и длину отрезка АВ, если: 1 А (3;-1), В
- 10. о I вариант Дано: А (3;-1), В (-2;4), точка М – середина АВ. Найти: IАВI, М(x;y).
- 11. Расстояние между точками A(x1; y1; z1) и B(x2; y2; z2) Координаты середины отрезка АВ, где A(x1;
- 12. Задача № 2. Дано: А (1;-1;2), В (3;1;-2) Найдите координаты середины отрезка АВ и его длину.
- 14. Скачать презентацию






 Модели и развёртки многогранников
Модели и развёртки многогранников Решение задач на работу
Решение задач на работу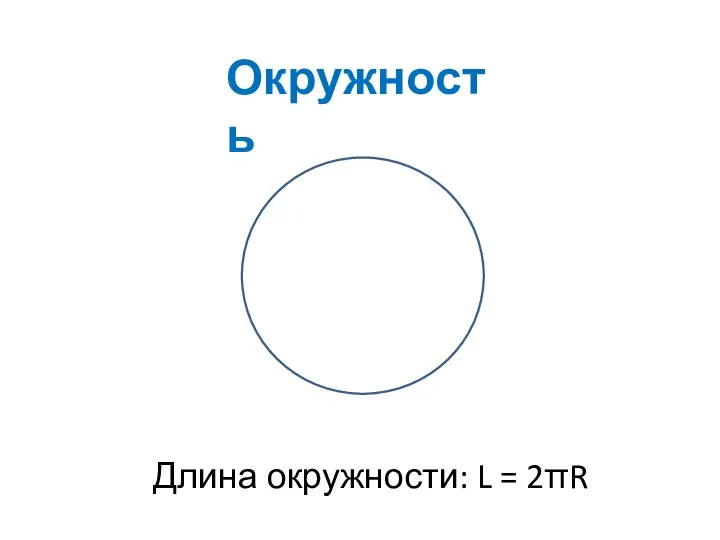 Числовая окружность
Числовая окружность Состав чисел в приделах 10. Решение задач
Состав чисел в приделах 10. Решение задач Дробно-линейная функция
Дробно-линейная функция Комплексные числа
Комплексные числа Интегрирование тригонометрических функций
Интегрирование тригонометрических функций Система управління технологічного процесу приготування розчинів для піроксилінових порохів
Система управління технологічного процесу приготування розчинів для піроксилінових порохів Векторы
Векторы Сечения куба,призмы и пирамиды
Сечения куба,призмы и пирамиды Подобие треугольников
Подобие треугольников Алгебра и начала анализа.10 класс
Алгебра и начала анализа.10 класс Правильная пирамида
Правильная пирамида Пропорция и проценты
Пропорция и проценты Сравнение рациональных чисел
Сравнение рациональных чисел История возникновения числа ПИ
История возникновения числа ПИ Тригонометрические уравнения. Однородные тригонометрические уравнения
Тригонометрические уравнения. Однородные тригонометрические уравнения Своя игра 2
Своя игра 2 Показательная функция. Показательные уравнения и неравенства
Показательная функция. Показательные уравнения и неравенства Презентация на тему Решение задач В ЕГЭ по теории вероятности
Презентация на тему Решение задач В ЕГЭ по теории вероятности  Презентация на тему Нумерация многозначных чисел (4 класс)
Презентация на тему Нумерация многозначных чисел (4 класс)  Комбинаторика
Комбинаторика Сложение, вычитание многочленов и умножение на одночлен
Сложение, вычитание многочленов и умножение на одночлен Презентация на тему Уравнение касательной
Презентация на тему Уравнение касательной  Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве Альтернативные издержки и кривая производственных возможностей
Альтернативные издержки и кривая производственных возможностей Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас
Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас Векторы. Задания
Векторы. Задания