Содержание
- 2. Для упрощения логических выражений используют законы алгебры логики. Они формулируются для базовых логических операций — «НЕ»,
- 3. Закон двойного отрицания означает, что операция «НЕ» обратима: если применить ее два раза, логическое значение не
- 4. Операции с константами и закон повторения легко проверяются по таблицам истинности операций «И» и «ИЛИ». Переместительный
- 5. Распределительный закон для операции «ИЛИ» — это обычное раскрытие скобок. А вот для операции «И» мы
- 6. ДОКАЗАТЕЛЬСТВО РАСПРЕДЕЛИТЕЛЬНОГО ЗАКОНА Доказательство можно начать с правой части, раскрыв скобки: (А + В) • (А
- 7. Равенство доказано. Мы доказали также и закон поглощения для операции «И» (для операции «ИЛИ» вы можете
- 8. Теперь с помощью приведённых законов алгебры логики упростим логическое выражение: (А • В • C) +
- 9. Алгоритм упрощения логических выражений: 1. Заменить все «небазовые» операции (исключающее ИЛИ, импликацию, эквивалентность и др.) на
- 10. Задачи. Упростите логические выражения:
- 12. Скачать презентацию









 Многогранники на службе у человека
Многогранники на службе у человека Логика
Логика Эмпирико-статистические модели климатических изменений. Земля как климатическая система
Эмпирико-статистические модели климатических изменений. Земля как климатическая система Старинные меры веса, длины и старинные денежные единицы (задачи для учащихся 5-6 классов)
Старинные меры веса, длины и старинные денежные единицы (задачи для учащихся 5-6 классов) Opredelenny_integral
Opredelenny_integral Распределительное свойства умножения
Распределительное свойства умножения Функциональная грамотность: формирование, диагностика
Функциональная грамотность: формирование, диагностика Арифметика в позиционных системах счисления
Арифметика в позиционных системах счисления Задача управления движением маятника
Задача управления движением маятника Презентация на тему Преобразование плоскости
Презентация на тему Преобразование плоскости  Домашнее задание. Решение задач
Домашнее задание. Решение задач Презентация на тему ПОНЯТИЕ ЛОГАРИФМА
Презентация на тему ПОНЯТИЕ ЛОГАРИФМА  _Лекция СА № 2 Структуры и распределения
_Лекция СА № 2 Структуры и распределения Приведение уравнений фигур к каноническому виду при помощи квадратичных форм
Приведение уравнений фигур к каноническому виду при помощи квадратичных форм подготовка к ВПР
подготовка к ВПР Духовно-нравственное воспитание на уроках математики
Духовно-нравственное воспитание на уроках математики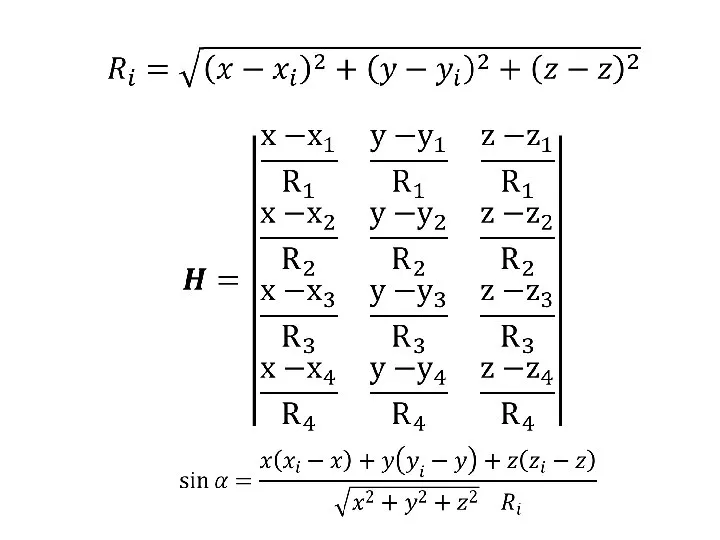 Геометрический фактор
Геометрический фактор Знакомьтесь, открытые задачи. Мастер-класс
Знакомьтесь, открытые задачи. Мастер-класс Декартова система координат
Декартова система координат Скалярное произведение векторов. тест
Скалярное произведение векторов. тест Сложение и вычитание целых чисел и десятичных дробей
Сложение и вычитание целых чисел и десятичных дробей Первый замечательный предел
Первый замечательный предел Сантиметр. Линейка
Сантиметр. Линейка Задачи по математике
Задачи по математике Умножение смешанных дробей
Умножение смешанных дробей Числа 6 и 7. Письмо цифры 6
Числа 6 и 7. Письмо цифры 6 Многогранники. Виды многогранников
Многогранники. Виды многогранников Обобщение по теме Четырехугольники
Обобщение по теме Четырехугольники