Содержание
- 2. Критерии оценивания знает определение критических точек функции; умеет находить критические точки функции; знает необходимое и достаточное
- 3. Возрастание и убывание функции Подняться на гору. Функция возрастает на интервале [b; a] При спуске с
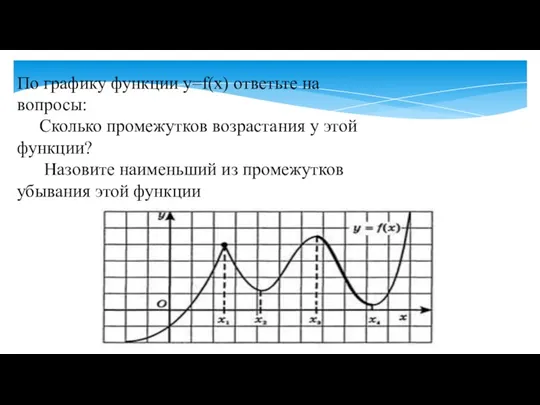
- 4. По графику функции y=f(x) ответьте на вопросы: Сколько промежутков возрастания у этой функции? Назовите наименьший из
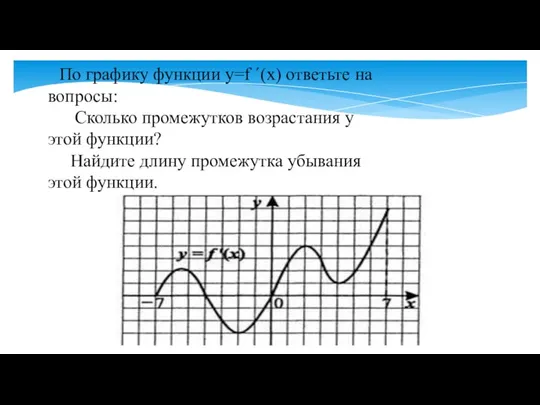
- 5. По графику функции y=f ´(x) ответьте на вопросы: Сколько промежутков возрастания у этой функции? Найдите длину
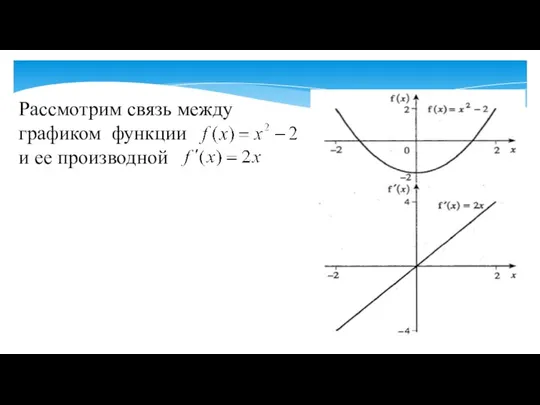
- 6. Рассмотрим связь между графиком функции и ее производной
- 7. 1. Множество точек х, где график производной функции располагается выше оси Ох, соответствует множеству точек х,
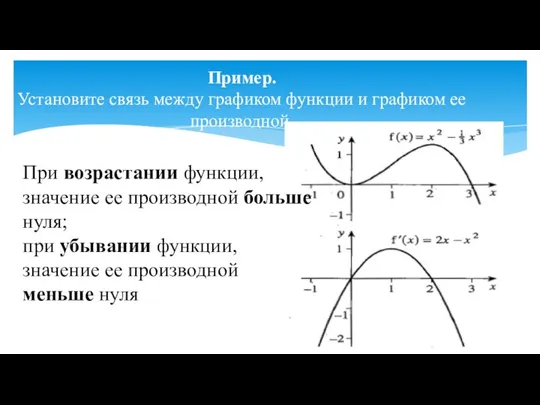
- 8. Пример. Установите связь между графиком функции и графиком ее производной. При возрастании функции, значение ее производной
- 9. Если производная некоторой непрерывной функции f(x) на некотором промежутке положительна (f '(x)>0), то на этом промежутке
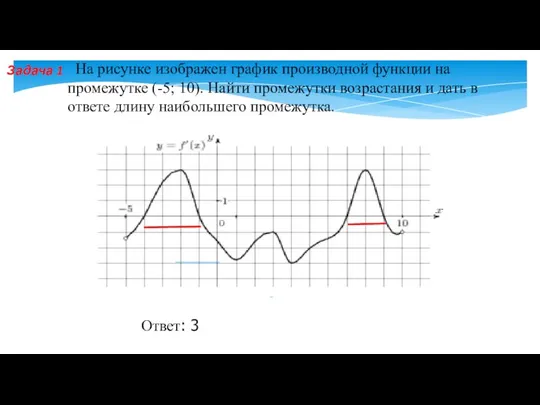
- 10. На рисунке изображен график производной функции на промежутке (-5; 10). Найти промежутки возрастания и дать в
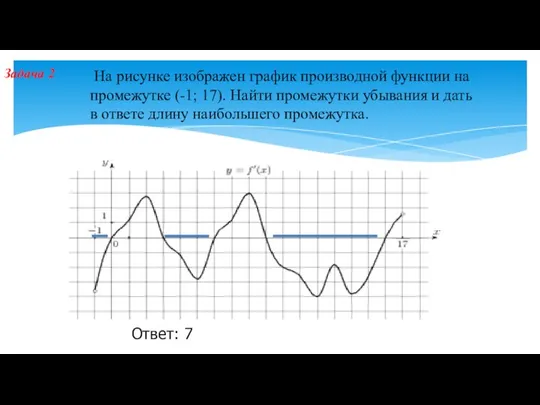
- 11. Ответ: 7 Задача 2 На рисунке изображен график производной функции на промежутке (-1; 17). Найти промежутки
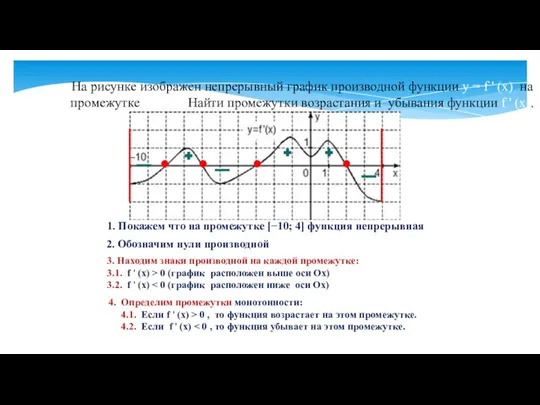
- 12. 2. Обозначим нули производной 4. Определим промежутки монотонности: 4.1. Если f ' (x) > 0 ,
- 13. Найдем область определения функции. Найдем производную функцию. Найдем нули производной. Методом интервалов определим знаки производной на
- 14. Найдите промежутки монотонности функции f(х) = х4 - 2х2 1. D(f) = R 2. f/(x) =
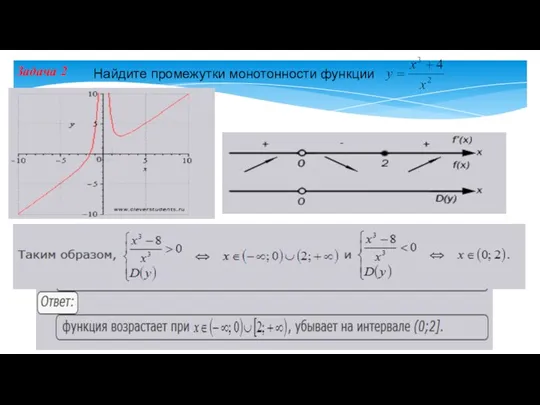
- 15. Задача 2 Найдите промежутки монотонности функции
- 17. Скачать презентацию






 ПРОЕКТ «КАК ИЗМЕРЯЛИ В СТАРИНУ»
ПРОЕКТ «КАК ИЗМЕРЯЛИ В СТАРИНУ» Решение задач
Решение задач Периметр прямоугольника. Площадь прямоугольника. Путь. (5 класс)
Периметр прямоугольника. Площадь прямоугольника. Путь. (5 класс) В мире плоскостей
В мире плоскостей Решение задач. 6 класс
Решение задач. 6 класс Треугольник и его элементы
Треугольник и его элементы Игра Верю - не верю
Игра Верю - не верю Перспективная модель ЕГЭ по математике
Перспективная модель ЕГЭ по математике Математическое путешествие в мир гармонии. Устный журнал
Математическое путешествие в мир гармонии. Устный журнал Живая планета!
Живая планета! Степень с натуральным и целым показателем
Степень с натуральным и целым показателем Числовые промежутки
Числовые промежутки Презентация на тему Функция у=х^2, её свойства и график
Презентация на тему Функция у=х^2, её свойства и график  Распределение случайных величин. Функция распределения и плотность распределения случайной величины
Распределение случайных величин. Функция распределения и плотность распределения случайной величины Осевая и центральная симметрия
Осевая и центральная симметрия Радианная Мера Угла
Радианная Мера Угла Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани
Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани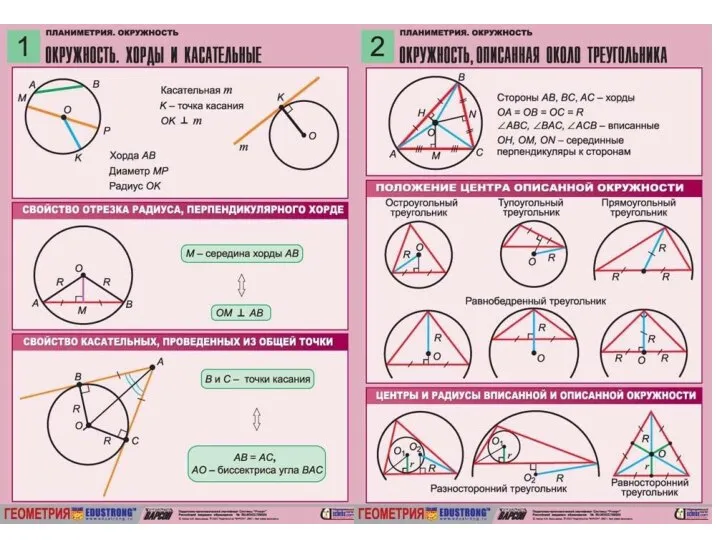 Геометрия. Конспекты
Геометрия. Конспекты Интегральное исчисление. Первообразная функция. Неопределённый интеграл
Интегральное исчисление. Первообразная функция. Неопределённый интеграл Ребуси Вавіліної Анастасії
Ребуси Вавіліної Анастасії Сумма бесконечной геометрической прогрессии
Сумма бесконечной геометрической прогрессии Презентация на тему Решение задач на нахождение неизвестного по двум разностям
Презентация на тему Решение задач на нахождение неизвестного по двум разностям  Теория погрешностей
Теория погрешностей Треугольники. Решение задач
Треугольники. Решение задач Определение неизвестного числа
Определение неизвестного числа Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Станция логическая. По тропинкам занимательной математики
Станция логическая. По тропинкам занимательной математики Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики
Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики